11.3: The Stirling Cycle

Last updated
Save as PDF

Page ID: 7279

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

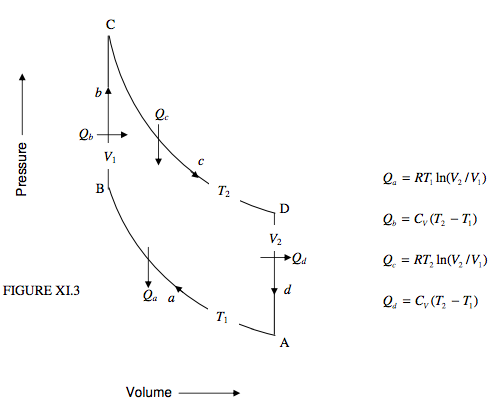
This takes place between two isotherms and two isochors. Note that, provided the working substance is an ideal gas, there is no change in the internal energy along the isotherms, and that the work done by or on the gas is equal to the heat gained by or lost from it. No work is done along the isochors. I show the cycle in the PV plane in figure XI.3, and an imaginary schematic engine in figure XI.4.

Screen Shot 2019-07-04 at 6.57.14 PM.png

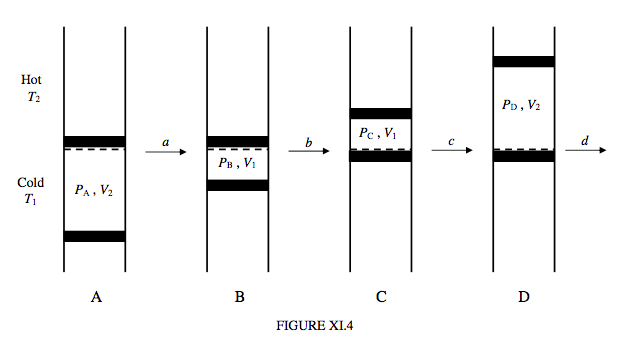
Screen Shot 2019-07-04 at 6.57.22 PM.png

The gas is supposed to be held in a cylinder between two pistons. The cylinder is divided into two sections by a porous partition. One section is kept at a hot temperature T₂ and the other is kept at a cold temperature T₁.

In stage a, the cold gas is compressed isothermally. The work done on a mole of the gas is RT₁ln(V₂/V₁); this is converted into heat, Q_a, which is lost from the gas to the cold reservoir.

In stage b, the gas, held at constant volume, is transferred to the hot reservoir. No work is done on or by the gas, but a quantity of heat Q_b = C_V(T₂ − T₁) per mole is supplied to the gas.

In stage c, the hot gas is expanded isothermally to its original volume. The work done by a mole of the gas is RT₂ln(V₂/V₁); in order to prevent the gas from cooling down, it has to absorb an equal amount of heat, Q_c from the hot reservoir. Note that Q_c> Q_a.

In stage d, the gas, held at constant volume, is transferred back to the cold reservoir. No work is done on or by the gas, but the gas loses a quantity of heat Q_d = C_V(T₂ − T₁) to the cold reservoir. Note that Q_d = Q_b.

Exercise: Show that the efficiency is

\[ \eta=\frac{R\left(T_{2}-T_{1}\right) \ln \left(V_{2} / V_{1}\right)}{C_{V}\left(T_{2}-T_{1}\right)+R T_{2} \ln \left(V_{2} / V_{1}\right)}.\]

If the gas is an ideal diatomic gas (to which air is an approximation), then \( C_{V}=\frac{5}{2} R\), and then

\[ \eta=\frac{\left(T_{2}-T_{1}\right) \ln \left(V_{2} / V_{1}\right)}{2.5\left(T_{2}-T_{1}\right)+T_{2} \ln \left(V_{2} / V_{1}\right)}.\]

If helium were used as an ideal gas, the efficiency would be greater, because for helium, \( C_{V}=\frac{3}{2} R\).