11.4: The Otto Cycle

Last updated
Save as PDF

Page ID: 7280

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The Otto cycle (to which the engine under the hood of your car bears some slight resemblance) works between two isochors and two adiabats (figure XI.5).

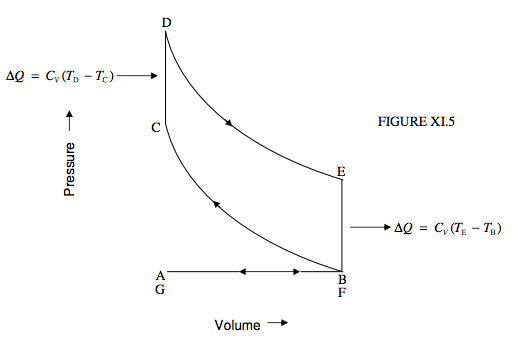
Screen Shot 2019-07-05 at 9.18.42 AM.png

The cycle starts at A. From A to B the piston recedes and a valve is open, so that a misture of air and petrol (gasoline) is drawn in at constant (atmospheric) pressure. The temperature is typically somewhat above ambient temperature because of the previous operation of the cycle. At B, the valve is closes, and now from B to C a fixed mass of gas is compressed adiabatically, the temperature being a few hundred K. C is the point of maximum compression. At this point a spark is struck and the mixture is ignited. In effect heat is added to the system and the temperature goes up instantaneously to perhaps 2000 K at constant (small) volume. The gas, now having reached D, expands adiabatically to E, doing work, and the temperature drops somewhat. At E, a (second) valve opens, gas is expelled, the pressure drops to atmospheric, and the temperature drops to its original value. We are now at F. The piston pushes the remaining gas out, and we end at G. The cycle starts anew.

It is left as an exercise to show:

Net work done by the engine per cycle = \(C_{V}\left(T_{\mathrm{D}}-T_{\mathrm{C}}\right)\left(1-\frac{T_{\mathrm{B}}}{T_{\mathrm{C}}}\right)\).

Volume of stroke = \( V_{\mathrm{B}}-V_{\mathrm{C}}=V_{\mathrm{B}}\left[1-\left(\frac{T_{\mathrm{B}}}{T_{\mathrm{C}}}\right)^{1 / \gamma-1 )}\right]\).

Maximum pressure = \( P_{\mathrm{D}}=P_{\mathrm{B}} \frac{T_{\mathrm{D}}}{T_{\mathrm{B}}}\left(\frac{T_{\mathrm{C}}}{T_{\mathrm{B}}}\right)^{1 /(\gamma-1)}\).

Efficiency = \(1-\left(\frac{V_{C}}{V_{\mathrm{B}}}\right)^{\gamma-1}=1-\frac{T_{\mathrm{B}}}{T_{\mathrm{C}}}\).

In principle the efficiency could be very large if the temperature at C, at the end of the adiabatic compression, were high. In practice the temperature at the end of the adiabatic compression is limited (and therefore so is the efficiency) because, if the temperature were too high, the air-gasoline mixture would ignite spontaneously.