15.2: Adiabatic Decompression
- Page ID
- 7306
We are going to calculate an expression for \((∂T/∂P)_S\). The expression will be positive, since T and P increase together. We shall consider the entropy as a function of temperature and pressure, and, with the variables
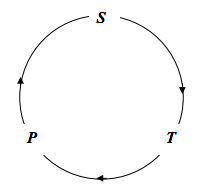
we shall start with the cyclic relation
\[\left(\frac{\partial S}{\partial T}\right)_{P}\left(\frac{\partial T}{\partial P}\right)_{S}\left(\frac{\partial P}{\partial S}\right)_{T}=-1. \label{15.2.1}\]
The middle term is the one we want. Let’s find expressions for the first and third partial derivatives in terms of things that we can measure.
In a reversible process \(dS = dQ/T\), and, in an isobaric process, \(dQ = C_PdT\). Therefore
\[ \left(\frac{\partial S}{\partial T}\right)_{p}=\frac{C_{p}}{T}.\]
Also, we have a Maxwell relation (Equation 12.6.16). \(\left(\frac{\partial S}{\partial P}\right)_{T}=-\left(\frac{\partial V}{\partial T}\right)_{P}\). Thus Equation \ref{15.2.1} becomes
\[\left(\frac{\partial T}{\partial P}\right)_{S}=\frac{T}{C_{P}}\left(\frac{\partial V}{\partial T}\right)_{P}. \label{15.2.2}\]
Check the dimensions of this. Note also that CP can be total, specific or molar, provided that V is correspondingly total, specific or molar. (∂T/∂P)S is, of course, intensive.
If the gas is an ideal gas, the equation of state is \(PV = RT\), so that
\[ \left(\frac{\partial V}{\partial T}\right)_{P}=\frac{R}{P}=\frac{V}{T}.\]
Equation \ref{15.2.2} therefore becomes
\[\left(\frac{\partial T}{\partial P}\right)_{S}=\frac{V}{C_{P}}.\]


