18.6: Specific Heat Capacities of Gases

Last updated
Save as PDF

Page ID: 7331

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

We have to consider the measurement of the specific heat capacity at constant pressure and at constant volume.

The most famous of the early experiments to measure directly the specific heat capacity of a gas at constant pressure were Regnault's experiments of around 1860. Gas from a large storage cylinder was passed at constant pressure (measured with a manometer) through a series of helical copper tubes. The first helix was immersed in a constant high-temperature bath, which, of course, warmed the gas up. The warm gas then continued its flow through a smaller helix, which was immersed in a small copper calorimeter filled with cold water. The gas, of course, cooled down, and the water in the calorimeter warmed up. The fall in temperature of the gas and the rise in temperature of the water were measured, and hence the specific heat capacity of the gas at constant pressure was calculated. While the principle of the experiment was simple and straightforward, its actual practical execution required an experimental skill of the very highest order.

The most famous of the early experiments to measure directly the specific heat capacity of a gas at constant volume is Joly's differential steam calorimeter of around 1890. Two equal hollow copper spheres were suspended from the arms of a balance. One of the spheres was filled with the gas under investigation; the other was evacuated (or at least as far as the vacuum technology of the day could achieve). The two spheres were surrounded by a chamber into which steam could be pumped. I'm not very good at art, but I'll try to indicate very schematically, in figure XVIII.1, what I am trying to describe.

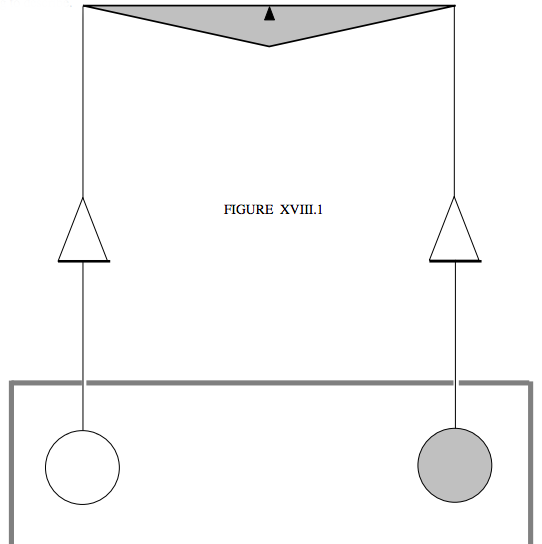
Steam was pumped into the chamber, and some of it condensed on the two spheres. Naturally, more steam condensed on the sphere that held the gas, and the mass of extra condensate was measured by adding weights to the other scale pan. The mass of extra condensate times its specific latent heat of condensation was equated to the heat required to raise the temperature of the gas inside the filled sphere from its initial room temperature to 100 °C. It was a brilliant experiment requiring superb experimental skill.