2.6: Sample problems and solutions
- Page ID
- 19622
During a physics lecture, you look under your seat and find a sheet containing data from an experiment on throwing balls vertically (perhaps a juggling experiment). The following equation is shown at the bottom of the sheet:
\(=\frac{v_{2}^{2}-v_{1}^{2}}{2a}\)
along with the following description:
- \(v_{1} =\) initial measured velocity of the ball m/s - various measurements.
- \(v_{2} =\) final measured velocity of the ball m/s - seems to be zero every time.
- \(a =\) acceleration of the ball \((−9.8\text{m/s}^{2})\).
Unfortunately, the students spilled ketchup on the left hand side of their equation, making it illegible. Luckily, you are proficient in dimensional analysis. What were the students trying to calculate, based on this model?
- Answer
-
We can use their equation to determine the dimension of the quantity on the left hand side:
\([?]=\frac{[v_{2}^{2}]-[v_{1}^{2}]}{[a]}=\frac{\frac{L}{T}^{2}-\frac{L}{T}^{2}}{\frac{L}{T^{2}}}=L\)
Thus, the dimension of the unknown quantity is length. Given the context, they were likely attempting to model the height at which a vertically thrown ball would travel before stopping.
Chelsea is preparing meticulously for her upcoming trip to Europe. Being a self-proclaimed “shop-a-holic” and physics lover, she wants to figure out how many pairs of shoes she can buy on vacation that will physically fit in her closet. Her closet is a walk-in closet with two entrance doors. Estimate the number of pairs of shoes that can fit in Chelsea’s closet.
- Answer
-
We start by estimating the volume of Chelsea’s closet as well as that of a pair of shoes. Chelsea’s closet is a “walk-in closet’ with two double doors. If we know the dimensions of the door, we can estimate the width and height of the closet. Estimating the average size of a large door to be \(1\)m\(×2\)m, one face of the close will have an area of \(4\text{m}^{2}\). If we estimate the depth of Chelsea’s closet to be about \(3\text{m}\), the volume of her closet is \(12\text{m}^{3}\)
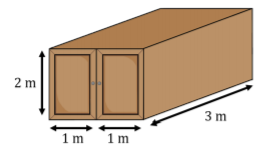
Figure \(\PageIndex{1}\): Chelsea's closet. Next, we can estimate the size of an average pair of shoes, by modeling a shoe as a rectangular box. A single shoe has a height and width of about \(5\) cm and a length of about \(25\) cm. A pair of shoes will thus be equivalent to box with dimensions \(5\)cm\(×10\)cm\(×25\)cm\(=1250\)cm\(^{3}\). This is equivalent to \(0.00125\text{m}^{3}\). We can now determine how many pairs of shoes, \(N\), would fit in the closet:
\(N=\frac{(12\text{m}^{3})}{(0.00125\text{m}^{3})}=9600\approx 10,000\)
We find that Chelsea can buy about \(10,000\) new pairs of shoes on her trip, and still fit them all into her closet. Time to get shopping, Chelsea!

