8.8: Sample problems and solutions
- Page ID
- 19419
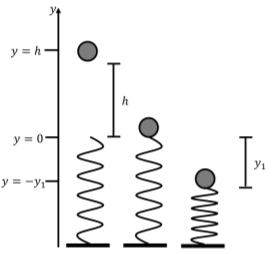
A ball of mass \(m\) is dropped onto a vertical spring with spring constant \(k\). The spring will compress until the ball comes to rest. How much will it compress if the ball is dropped from a height \(h\) above the spring?
- Answer
-
The two forces acting on the ball are gravity and the spring force. Both are conservative, so we can use conservation of mechanical energy. We will find the energy of the ball when it is at a height \(h\) above the spring, and the energy of the ball when the spring is fully compressed. Then, we will use conservation of mechanical energy to determine the compression of the spring.
Remember that the total mechanical energy is the sum of the total potential energy and the kinetic energy, \(E=U+K\). Let’s call the initial position of the ball \(A\) and the final position of the ball \(B\). You will notice that we set up our coordinate system so that \(y\) is positive upwards, with \(y=0\) at the point where the ball comes into contact with the spring. We choose to define both the gravitational potential energy and spring potential energy so that they are zero at \(y=0\).
Since the ball starts from rest, its kinetic energy is zero at position \(A\). At this point, the ball is not touching the spring, so the potential energy from the spring force is zero. The mechanical energy of the ball at position \(A\) is simply equal to its gravitational potential energy:
\[\begin{aligned} E_A&=U_A+K_A\\[4pt] E_A&=mgh\end{aligned}\]
At position \(B\), the ball is again at rest, so the kinetic energy of the ball is zero. Now that the ball is in contact with the spring, it will experience a force from the spring that can be modeled with a potential energy \(U(y)=\frac{1}{2}ky_1^2\), where \(y_1\) is the distance between the rest position of the spring and its compressed length. At point \(B\) (\(y=-y_1\)), the ball will have both spring and gravitational potential energy, so its mechanical energy at position \(B\) is given by:
\[\begin{aligned} E_B&=U_B+K_B=U_B\\[4pt] U_B&=mg(-y_1)+\frac{1}{2}ky_1^2\\[4pt] E_B&=-mgy_1+\frac{1}{2}ky_1^2\end{aligned}\]
Since mechanical energy is conserved in this system (no non-conservative forces are doing work), we can now set \(E_A=E_B\) and solve for \(y_1\):
\[\begin{aligned} E_A&=E_B\\[4pt] mgh&=-mgy_1+\frac{1}{2}ky_1^2\\[4pt] 0&=\frac{1}{2}ky_1^2-mgy_1-mgh\\[4pt]\end{aligned}\]
where in the last line we rewrote the expression as a quadratic equation. We can solve for \(y_1\) with the quadratic formula:
\[\begin{aligned} y_1=\frac{mg\pm\sqrt{(mg)^2-4(1/2k)(-mgh)}}{k}\\[4pt] y_1=\frac{mg\pm\sqrt{mg(mg+2kh)}}{k}\end{aligned}\]
We now have an expression for the amount the spring is compressed, \(y_1\), in terms of our known values.
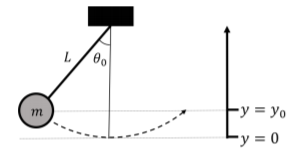
A simple pendulum consists of a mass \(m\) connected to a string of length \(L\). The pendulum is released from an angle \(\theta_0\) from the vertical. Use conservation of energy to find an expression for the velocity of the mass as a function of the angle.
- Answer
-
We are going to find a general expression for the energy of the system, and then use this expression to find the velocity at any point. There are two forces acting on the mass:
The force of tension (from the string). This force is perpendicular to the direction of motion at any point, so it does no work on the mass.
The force of gravity, which has a potential energy function given by \(U(y)=mgy\). We choose the gravitational potential energy to be zero when the pendulum hangs vertically (when \(\theta=0\) and \(y=0\)).
The mechanical energy of the mass is conserved, and at any point is given by the sum of its kinetic and its gravitational potential energies:
\[\begin{aligned} E=mgy+\frac{1}{2}mv^2\end{aligned}\]
We want to find the velocity as a function of \(\theta\), so we need to write \(y\) in terms of \(\theta\). As you may recall from Problem 7.6.2, we saw that from the geometry of the problem, we can express the height of the mass as \(y=L-L\cos\theta\), or \(L(1-\cos\theta)\), where \(y\) is the height as measured from the bottom point of the motion. You can refer to Figure 7.6.4 to refresh your memory. The energy at any point is then:
\[\begin{aligned} E=mgL(1-\cos\theta)+\frac{1}{2}mv^2\end{aligned}\]
Conservation of energy tells us that the total energy at any point must be the same as the initial energy. So, we can use our initial conditions to find the total energy of the system. The mass starts from rest (initial kinetic energy is zero) an angle \(\theta_0\) above the vertical:
\[\begin{aligned} E&=mgL(1-\cos\theta)+\frac{1}{2}mv^2\\[4pt] E_{initial}&=mgL(1-\cos\theta_0)\end{aligned}\]
Now that we have found the total energy of the system, we can write our general expression for the energy of the system at any point:
\[\begin{aligned} E&=mgL(1-\cos\theta)+\frac{1}{2}mv^2\\[4pt] mgL(1-\cos\theta_0)&=mgL(1-\cos\theta)+\frac{1}{2}mv^2\end{aligned}\]
All that’s left to do is simplify the expression and rearrange for \(v\):
\[\begin{aligned} mgL(1-\cos\theta_0)&=mgL(1-\cos\theta)+\frac{1}{2}mv^2\\[4pt] gL(1-\cos\theta_0)-gL(1-\cos\theta)&=\frac{1}{2}v^2\\[4pt] gL-gL\cos\theta_0-gL+gL\cos\theta&=\frac{1}{2}v^2\\[4pt] gL(\cos\theta-\cos\theta_0)&=\frac{1}{2}v^2\\[4pt] \therefore v&=\sqrt{2gl(\cos\theta-\cos\theta_0)}\end{aligned}\]
Discussion
We can see from this expression that the speed will be maximized when \(\cos\theta\) is maximized, which will occur when \(\theta=0\) (when the pendulum is vertical). This is as we expected. We can also see that we will get an imaginary number if the magnitude of \(\theta\) is greater than \(\theta_0\), showing that the motion is constrained between \(-\theta_0\) and \(\theta_0\). Finally, we showed that the velocity of the pendulum does not depend on the mass!
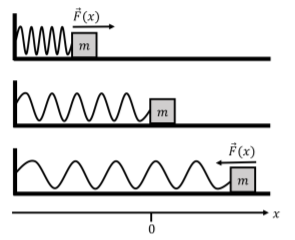
A block of mass \(m\) sits on a frictionless horizontal surface. It is attached to a wall by a spring with a spring constant \(k\). The mass is pushed so as to compress the spring and then it is released (Figure \(\PageIndex{3}\)). Use the Lagrangian formalism to find an equation of motion for the mass/spring system (i.e. use the Lagrangian to determine the acceleration of the mass).
- Answer
-
We are going to find an equation of motion of the system using the Lagrangian method. We choose to use a one dimension coordinate system, with the \(x\) axis defined to be co-linear with the spring, positive in the direction where the spring is extended, and set the origin to be located at the rest position of the spring. The kinetic energy and potential energy of the mass are given by
\[\begin{aligned} K&=\frac{1}{2}mv_x^2\\[4pt] U&=\frac{1}{2}kx^2\end{aligned}\]
since the only force exerted on the mass that can do work is the force from the spring. We have chosen the potential energy to be zero at \(x=0\). The Lagrangian for this system is:
\[\begin{aligned} L&=K-U\\[4pt] L&=\frac{1}{2}mv_x^2-\frac{1}{2}kx^2\end{aligned}\]
The Euler-Lagrange equation in one dimension is:
\[\begin{aligned} \frac{d}{dt}\left(\frac{\partial L}{\partial v_{x}}\right)-\frac{\partial L}{\partial x} = 0\end{aligned}\]
We can calculate the terms of the Euler-Lagrange equation:
\[\begin{aligned} \frac{\partial L}{\partial v_{x}}&=\frac{\partial}{\partial v_{x}}\left(\frac{1}{2}mv_x^2-\frac{1}{2}kx^2\right)\\[4pt] &=mv_x\\[4pt] \therefore \frac{d}{dt}\left(\frac{\partial L}{\partial v_{x}}\right)&=\frac{d}{dt}(mv_x)\\[4pt] &=ma_x\\[4pt] \textrm{and}\qquad \frac{\partial L}{\partial x}&=\left(\frac{1}{2}mv_x^2-\frac{1}{2}kx^2\right)\\[4pt] &=-kx\end{aligned}\]
and then put them together to get:
\[\begin{aligned} \frac{d}{dt}\left(\frac{\partial L}{\partial v_{x}}\right)-\frac{\partial L}{\partial x} &= 0\\[4pt] \therefore ma_x&=-kx\\[4pt]\end{aligned}\]
We can see that this equation of motion is equivalent to Newton’s Second Law.

