9.1: Kepler’s Laws
- Page ID
- 19421
Although humans have long been fascinated by the motion of objects in the sky, it was Johannes Kepler, in the early seventeenth century, that was the first to write down quantitative rules that described the motion of planets around the Sun. His theory was based on the extensive and detailed observations recorded by Tycho Brahe in the late sixteenth century.
Kepler proposed three laws that describe all of the data that Tycho Brahe had collected about planetary motion:
- The path of a planet around the Sun is described by an ellipse with the Sun at once of its foci.
- All planets move in such a way that the area swept by a line connecting the planet and the Sun in a given period of time is constant.
We examine these three laws in more detail in the sections that follow. It should also be noted that, even though Kepler’s Laws were derived for planets orbiting the Sun, they apply to any body that is orbiting any other body under the influence of gravity1.
Kepler’s First Law
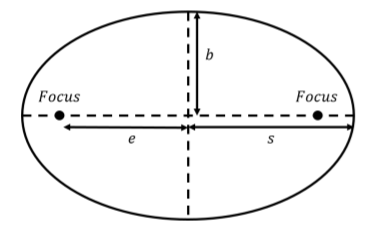
Kepler noticed that the motion of all planets followed the path of an ellipse with the Sun located at one of its foci. Figure \(\PageIndex{1}\) shows a diagram of an ellipse, along with its two foci, its semi-major axis, \(s\), its semi-minor axis, \(b\), and its eccentricity, \(e\). The eccentricity is a measure of how far a focus is from the center of the ellipse. A larger eccentricity thus corresponds to a “flatter” ellipse. Note that a circle is just a special case of an ellipse, with both foci located at the center of the circle.
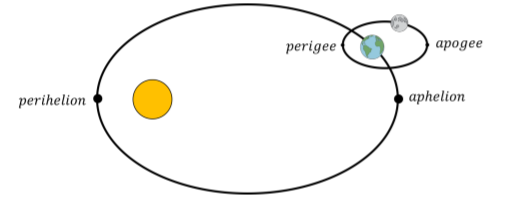
The sun is located at one of the foci. The point of closest approach to the Sun is called the “perihelion” of the orbit (or “perigee” if the orbit is not around the Sun), and the point furthest from the Sun is called the “aphelion” of the orbit (or “apogee” if the orbit is not around the Sun), as shown in Figure \(\PageIndex{2}\).
Order the ellipses from smallest eccentricity to largest eccentricity.
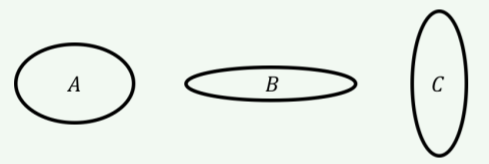
- Answer
-
\(A<C<B\)
Kepler’s Second Law
Kepler’s Second Law is really a statement about the speed of a planet in an elliptical orbit. It states that the area swept by a line connecting the planet and the Sun in a given period of time is fixed. This is illustrated in Figure \(\PageIndex{4}\), which shows the elliptical orbit of a planet around the Sun located at one of the foci, and the area swept out when the planet goes from \(A\) to \(B\) and from \(C\) to \(D\).
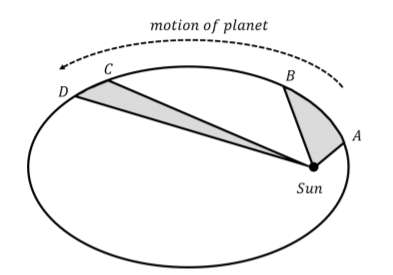
Kepler’s Second Law states that the two areas that are shown by the grayed out sections in the figure are the same if the planet took the same amount of time to travel between points \(A\) and \(B\) as it did to travel between points \(C\) and \(D\). Because the points \(C\) and \(D\) are further away from the Sun than points \(A\) and \(B\), the distance between points \(C\) and \(D\) must be smaller than the distance between points \(A\) and \(B\) for the two areas to be the same. This, in turn, implies that the planet must be moving slower between \(C\) and \(D\) than between points \(A\) and \(B\). The speed of a planet is thus greatest at the perihelion and smallest at the aphelion. As we will see in a later chapter, Kepler’s Second Law is equivalent to the statement that the angular momentum of the planet about the Sun is conserved.
Based on Kepler’s second law, what can you say about the speed of a planet in a circular orbit?
- Answer
-
The speed of the planet is constant.
Kepler’s Third Law
Kepler’s Third Law is quantitative and relates the orbital periods (\(T\)) and the semi-major axes (\(s\)) between any two planets in orbit around the Sun:
\[\begin{aligned} \left(\frac{T_1}{T_2}\right)^2=\left(\frac{s_1}{s_2}\right)^3\end{aligned}\]
We can re-arrange this relation so that all of the quantities related to one planet are on the same side of the equal sign:
\[\begin{aligned} \frac{T_1^2}{s_1^3}=\frac{T_2^2}{s_2^3}=\text{constant}\end{aligned}\]
In other words, the ratio between the orbital period squared and the semi-major axis cubed is a constant, independent of the particular planet. In Example 9.2.2, we will use Newton’s Universal Theory of Gravity to evaluate the constant.
An object is in a circular orbit with radius \(r\) and has an orbital speed \(v\). If you double the radius of the circular orbit, what will be the value of the orbital speed?
- \(2v\)
- \(8v\)
- \(\sqrt{8}v\)
- \(\frac{1}{\sqrt{2}}v\)
- Answer
- D.
1. In fact, they apply for any two bodies orbiting each other if the force between them is an “inverse-square” law, such as the gravitational and electric forces.

