12.1: Rotational Kinetic Energy of an Object

In this section, we show how to define the rotational kinetic energy of an object that is rotating about a stationary axis in an inertial frame of reference. Consider a solid object that is rotating about an axis with angular velocity, \(\vec\omega\), as depicted in Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\): An object rotating about an axis that is perpendicular to the page.

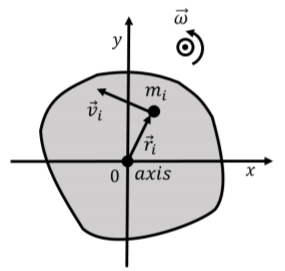
We can model the object as being composed of many point particles, each with a mass \(m_i\), located at a position \(\vec r_i\), with velocity \(\vec v_i\) relative to the axis of rotation. We choose a coordinate system whose origin is on the axis of rotation and whose \(z\) axis is co-linear with the axis of rotation, as depicted in Figure \(\PageIndex{1}\).

Each particle of mass \(m_i\) in the object has a kinetic energy, \(K_i\):

\[\begin{aligned} K_i = \frac{1}{2}m_iv_i^2\end{aligned}\]

We can sum the kinetic energy of each particle together to get the total rotational kinetic energy, \(K_{rot}\), of the object:

\[\begin{aligned} K_{rot} = \sum_i \frac{1}{2}m_iv_i^2\end{aligned}\]

Although each particle will have a different velocity, \(\vec v_i\), they will all have the same angular velocity, \(\vec\omega\). For any particle, located a distance \(r_i\) from the axis of rotation, their velocity is related to the angular velocity of the object by:

\[\begin{aligned} \vec v_i &= \vec \omega \times \vec r_i\\[4pt] v_i &= \omega r_i\end{aligned}\]

where \(\vec \omega\) and \(\vec r_i\) are always perpendicular to each other, since \(\vec\omega\) is out of the plane of the page. Furthermore, the velocity vector, \(\vec v_i\), will always be perpendicular to \(\vec r_i\), since all particles are moving in circles centerd about the axis of rotation. We can thus write the total rotational kinetic energy of the object using the angular speed:

\[\begin{aligned} K_{rot} &= \sum_i \frac{1}{2}m_iv_i^2 = \sum_i \frac{1}{2}m_ir_i^2\omega^2= \frac{1}{2} \omega^2 \sum_i m_ir_i^2\\[4pt] &=\frac{1}{2}I\omega^2\end{aligned}\]

where we factored \(\omega\) and the one half out of the sum, as these are the same for each particle \(i\). We then recognized that the remaining sum is simply the definition of the object’s moment of inertia about the axis:

\[\begin{aligned} I = \sum_i mr_i^2\end{aligned}\]

Thus, the rotational kinetic energy of an object rotating with angular speed \(\omega\) about an axis that is stationary in an inertial frame of reference is given by:

\[K_{rot} = \frac{1}{2}I\omega ^{2}\]

where \(I\) is the object’s moment of inertia about that axis. The rotational kinetic energy is functionally very similar to the linear kinetic energy; instead of mass, we use the moment of inertia, and instead of speed squared, we use angular speed squared.

Work on a rotating object

We can calculate the work done by a force exerted on an object rotating about a stationary axis in an inertial frame of reference. Let \(\vec F\) be a force exerted at position, \(\vec r\), relative to the axis of rotation at some instant in time, and let the force be exerted in the plane perpendicular to the axis of rotation, as illustrated in Figure \(\PageIndex{2}\). Because the object is rotating about the given axis, only the component of the force that is tangent to the circle about which the point where the force is exerted can do work (only the component of the force that is parallel to the displacement can do work).

The work done by the force as the object rotates by a certain angle is given by:

\[\begin{aligned} W = \int \vec F \cdot d\vec l = \int F_\perp dl\end{aligned}\]

where \(d\vec l\) is a small displacement along the (circular) path followed by the point where the force is exerted, as illustrated in Figure \(\PageIndex{2}\). \(F_\perp\) is the component of \(\vec F\) that is perpendicular to the vector, \(\vec r\), from the axis of rotation to the location where the force is exerted (\(F_\perp\) is the component of \(\vec F\) that is tangent to the circle).

Figure \(\PageIndex{2}\): Calculating the work done by a force on a rotating object.

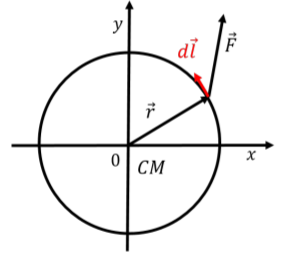
At some instant in time, when the force is exerted at position, \(\vec r\), consider the scalar product between the torque from the force, \(\vec \tau\), and an infinitesimal angular displacement, \(d\vec \theta\), about the axis of rotation:

\[\begin{aligned} \vec\tau \cdot d\vec\theta = (\vec r \times \vec F) \cdot \left(\frac{1}{r^2} \vec r\times d\vec l\right)\end{aligned}\]

The vectors \(\vec \tau\) and \(d\vec \theta\) are parallel to the axis of rotation (because \(\vec F\) and \(d\vec l\) are in the plane perpendicular to the axis of rotation), so their scalar product will be equal to the product of their magnitudes. The vector \(\vec r \times \vec F\) has a magnitude of:

\[\begin{aligned} \vec r \times \vec F = rF_\perp\end{aligned}\]

where \(F_\perp\) is the component of the force tangent to the circle. The vector \(\vec r\times d\vec l\) has a magnitude:

\[\begin{aligned} \vec r\times d\vec l = rdl\end{aligned}\]

since \(\vec r\) and \(d\vec l\) are always perpendicular. The scalar product \(\vec\tau \cdot d\vec\theta\) is thus equal to:

\[\begin{aligned} \vec\tau \cdot d\vec\theta = rF_\perp \frac{1}{r^2} rdl = F_\perp dl\end{aligned}\]

The work done by a force when an object rotates about an axis can thus be written in terms of its torque about that axis and the corresponding angular displacement from \(\theta_1\) to \(\theta_2\):

\[W=\int_{\theta _{1}}^{\theta _{2}}\vec\tau\cdot f\vec\theta \]

The net work done on an object through an angular displacement from \(\theta_1\) to \(\theta_2\) can thus be written using the net torque \(\vec \tau^{net}\) exerted on the object:

\[\begin{aligned} W^{net} = \int_{\theta_1}^{\theta_2}\vec\tau^{net}\cdot d\vec \theta\end{aligned}\]

We can re-arrange this using Newton’s Second Law for rotational dynamics:

\[\begin{aligned} \vec\tau^{net} &= I \vec\alpha\\[4pt] &= I \frac{d\vec\omega}{dt} = I \frac{d\omega}{d\theta}\frac{d\vec\theta}{dt}=I \frac{d\omega}{d\theta} \vec\omega\end{aligned}\]

which allows us to write the integral over a change in angular velocity instead of angular displacement:

\[\begin{aligned} W^{net} &= \int_{\theta_1}^{\theta_2}\vec\tau^{net}\cdot d\vec \theta = \int_{\theta_1}^{\theta_2}I \frac{d\omega}{d\theta} \vec\omega \cdot d\vec \theta\\[4pt] &=\int_{\omega_1}^{\omega_2}I \omega d\omega = \frac{1}{2}I\omega_2^2 - \frac{1}{2}I\omega_1^2\end{aligned}\]

where we used the fact that \(\vec\omega\) are \(d\vec\theta\) are parallel. We thus find that the Work-Energy Theorem can also be applied to find the change in rotational kinetic energy resulting from the net work done by a torque:

\[W^{net} = \int_{\theta _{1}}^{\theta _{2}}\vec\tau ^{net}\cdot d\vec\theta = \Delta K_{rot}\]

If a constant torque, \(\vec\tau\), is exerted on an object that is rotating at constant angular velocity, \(\vec\omega\), then the rate at which that work is being done is given by:

\[\begin{aligned} P = \frac{dW}{dt} = \frac{d}{dt} \vec \tau \cdot d\vec\theta = \vec \tau \cdot \frac{d\vec\theta}{dt} = \vec \tau \cdot \vec\omega\end{aligned}\]

This is very similar to the power, \(P=\vec F\cdot \vec v\), with which a force does work on an object moving with constant velocity, except that instead of force we use torque, and instead of velocity, we use angular velocity.

Total kinetic energy of an object

In the frame of reference of the center of mass, an object rotating about an axis through its center of mass with angular velocity, \(\vec \omega\), will have rotational kinetic energy, \(K_{rot}\), given by:

\[\begin{aligned} K_{rot}=\frac{1}{2}I_{CM}\omega^2\end{aligned}\]

where \(I_{CM}\) is the moment of inertia of the object about the axis through its center of mass.

We wish to determine the kinetic energy of the object in an inertial frame of reference where the object’s center of mass is moving with a velocity \(\vec v_{cm}\); that is, in a frame where the axis of rotation is moving with the velocity of the center of mass. We model the object as being composed of particles of mass, \(m_i\), each located at position, \(\vec r_i\), relative to the axis of rotation through the center of mass. The velocity, \(\vec v_i\), of a particle \(i\), in this frame of reference, is given by:

\[\begin{aligned} \vec v_i = \vec\omega \times \vec r_i + \vec v_{CM}\end{aligned}\]

where \(\vec\omega \times \vec r_i\) is the velocity of the particle as seen in the center of mass (due to rotation). The kinetic energy of particle \(i\), \(K_i\), is given by:

\[\begin{aligned} K_i = \frac{1}{2}m_iv_i^2 = \frac{1}{2}m_i(\vec v_i\cdot \vec v_i)\end{aligned}\]

where we expressed the speed of the particle squared using a scalar product of the velocity of the particle with itself. The total kinetic energy of the object is found by summing the kinetic energies of all of the particles:

\[\begin{aligned} K_{tot} &= \sum \frac{1}{2}m_i(\vec v_i\cdot \vec v_i) \\[4pt] &=\frac{1}{2} \sum_i m_i (\vec\omega \times \vec r_i + \vec v_{CM}) \cdot (\vec\omega \times \vec r_i + \vec v_{CM})\\[4pt] &=\frac{1}{2} \sum_i m_i (\vec\omega \times \vec r_i)\cdot(\vec\omega \times \vec r_i ) + \frac{1}{2} \sum_i m_i (\vec v_{CM}) \cdot (\vec v_{CM}) + \sum_i m_i (\vec\omega \times \vec r_i) \cdot (\vec v_{CM})\\[4pt] &=\frac{1}{2} \sum_i m_i \omega^2r_i^2 + \frac{1}{2} \sum_i m_i v_{CM}^2 + \sum_i m_i (\vec\omega \times \vec r_i) \cdot (\vec v_{CM})\\[4pt] &=\frac{1}{2} I_{CM}\omega ^2 + \frac{1}{2}M v_{CM}^2+\sum_i m_i (\vec\omega \times \vec r_i) \cdot (\vec v_{CM})\end{aligned}\]

where the first term is the rotational kinetic energy that we found earlier. The second term, called the “translational kinetic energy”, can be thought of as the kinetic energy of the whole system with mass \(M=\sum m_i\), due to the translational motion of the center of mass. The last term is identically zero; we can re-order the scalar product and factor \(\vec v_{CM}\) out of the sum:

\[\begin{aligned} \sum_i m_i (\vec\omega \times \vec r_i) \cdot (\vec v_{CM}) &= (\vec v_{CM}) \cdot \sum_i m_i (\vec\omega \times \vec r_i)\\[4pt] &=(\vec v_{CM}) \cdot \sum_i m_i \vec v'_{i}\end{aligned}\]

where \(v'_{i} = \vec\omega \times \vec r_i\) is the velocity of particle \(i\) in the center of mass frame of reference. But the sum:

\[\begin{aligned} \sum_i m_i \vec v'_{i}\end{aligned}\]

is the numerator for the definition of the velocity of the center of mass, which, in the center of mass frame of reference is identically zero!

Thus, the total kinetic energy of an object of mass, \(M\), that is rotating about an axis through its center of mass with angular velocity, \(\omega\), and whose center of mass is moving with velocity, \(\vec v_{CM}\), is given by:

\[K_{tot}=K_{rot}+K_{trans}=\frac{1}{2}I_{CM}\omega ^{2}+\frac{1}{2}Mv^{2}_{CM}\]

The total kinetic energy can be thought of as the sum of the rotational and kinetic energies.