Skip to main content
Physics LibreTexts

14.1: Characteristics of a wave

  1. Last updated
  2. Save as PDF
  • Page ID
    19461

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Definition and types of waves

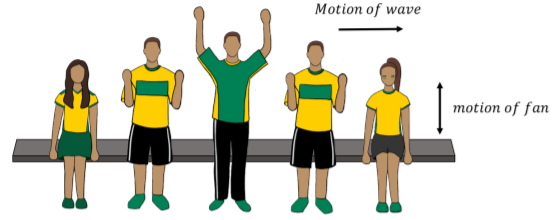
    A traveling wave is a disturbance that travels through a medium. Consider the waves made by fans at a soccer game, as in Figure \(\PageIndex{1}\). The fans can be thought of as the medium through which the wave propagates. The elements of the medium may oscillate about an equilibrium position (the fans move a short distance up and down), but they do not travel with the wave (the fans do not move horizontally with the wave).

    clipboard_e77bbb20962e6ab030aaf32a367c4d05e.png
    Figure \(\PageIndex{1}\): A transverse wave made by soccer fans moving up and down.

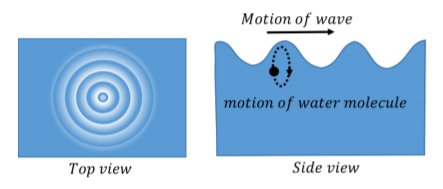
    Consider the ripples (waves) made by a rock dropped in a pond (Figure \(\PageIndex{2}\)). The ripples travel outwards from where the rock was dropped, but the water itself does not move outwards. The individual water molecules will move in small circles about an equilibrium position, but they do not move along with the waves.

    clipboard_e5e14ac86fd22638052932836e695ca12.png
    Figure \(\PageIndex{2}\): A transverse wave traveling through water. The left panel shows the view from above as ripples move outwards. The right panel shows the motion of an individual water molecule as the wave is viewed from the side.

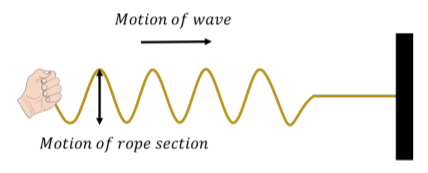
    We can distinguish between two classes of waves, based on the motion of the medium through which it propagates. With transverse waves, the elements of the medium oscillate back and forth in a direction perpendicular to the motion of the wave. For example, if you attach a horizontal rope to a wall and move the other end up and down (Figure \(\PageIndex{3}\)), you can create a disturbance (a wave) that travels horizontally along the rope. The parts of the rope do not move horizontally; they only move up and down, about some equilibrium position.

    clipboard_e52c2219781e0b9f52506abc1a2a063d2.png
    Figure \(\PageIndex{3}\): A transverse wave traveling through a rope. The wave is created by moving one end of the rope up and down.

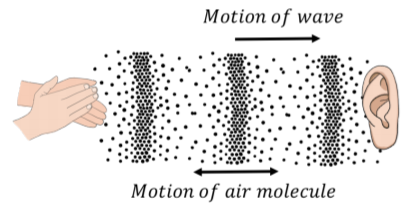
    With longitudinal waves, the elements of the medium oscillate back and forth in the same direction as the motion of the wave. If you clap your hands, you will create a pressure disturbance in the air that will propagate; this is what we call sound (a sound wave). The air molecules oscillate about an equilibrium position in the same direction as the wave propagates, but they do not move with the wave.

    clipboard_e4874b9b8ee9c77f83489d037651273ea.png
    Figure \(\PageIndex{4}\): A longitudinal sound wave traveling through the air. The air molecules move back and forth in the same direction as the wave, but they oscillate about an equilibrium position instead of moving with the wave​​​​​​​.

    Furthermore, we can distinguish between “travelling waves”, in which a disturbance propagates through a medium, and “standing waves”, which do not transport energy through the medium (for example, a vibrating string on a violin).

    Exercise \(\PageIndex{1}\)

    Are the waves propagating through a slinky when you compress and elongate it (Figure \(\PageIndex{5}\)) transverse or longitudinal?

    clipboard_ea650c681a3808115af3e8ba8bc889baa.png
    Figure \(\PageIndex{5}\): A wave traveling through a slinky. The wave is created when you compress or elongate the slinky
    1. Transverse
    2. Longitudinal
    Answer

    Physically, a wave can only propagate through a medium if the medium can be deformed. When a particle in the medium is disturbed from its equilibrium position, it will experience a restoring force that acts to bring it back to its equilibrium position. Often, if the displacement of the particle from the equilibrium is small, the magnitude of that force is proportional to the displacement. Thus, as we will see, we can model the propagation of waves by treating the particles in the medium as simple harmonic oscillators.

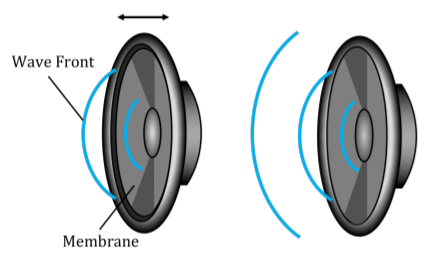
    A source of energy is required in order to deform the medium and generate a wave. For example, that source of energy could be a speaker creating sound waves by pushing a membrane back and forth; speakers require energy, and are often rated by the electrical power that they convert into sound waves (e.g. a \(50\text{W}\) speaker consumes \(50\text{W}\) of electrical power to produce sound).

    clipboard_eea86817e14631709d02a2a140cccc02d.png
    Figure \(\PageIndex{6}\): A speaker creating sound sound waves. The membrane vibrates back and forth which deforms the air to create sound waves that propagate through the air.

    Description of a wave

    In this chapter, we will mostly discuss how to describe sinusoidal waves; those for which the displacement of particles in the medium can be described by a sinusoidally-varying function of position. As we will see, more complicated waves can always be described as if they are the combination of multiple sine waves. We can use several quantities to describe a traveling wave, which are illustrated in Figure \(\PageIndex{7}\):

    • The wavelength, \(\lambda\), is the distance between two successive maxima (“peaks”) or minima (“troughs”) in the wave.
    • The amplitude, \(A\), is the maximal distance that a particle in the medium is displaced from its equilibrium position.
    • The velocity, \(\vec v\), is the velocity with which the disturbance propagates through the medium.
    • The period, \(T\), is the time it takes for two successive maxima (or minima) to pass through the same point in the medium.
    • The frequency, \(f\), is the inverse of the period (\(f=1/T\)).
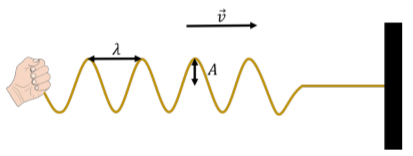
    clipboard_e192ad7e48e20e129d77c76e067072fda.png
    Figure \(\PageIndex{7}\): Wavelength, velocity, and amplitude for a transverse wave on a rope.

    The wavelength, speed, and period of the wave are related, since the amount of time that it takes for two successive maxima of the wave to pass through a given point will depend on the speed of the wave and the distance between maxima, \(\lambda\). Since it takes a time, \(T\), for two maxima a distance \(\lambda\) apart to pass through a given point in the medium, the speed of the wave is given by:

    \[v=\frac{\lambda}{T}=\lambda f\]

    Thus, of the three quantities (speed, period/frequency, and wavelength), only two are independent, as the third quantity must depend on the value of the other two. The speed of a wave depends on the properties of the medium through which the wave propagates and not on the mechanism that is generating the wave. For example, the speed of sound waves depends on the pressure, density, and temperature of the air through which they propagate, and not on what is making the sound. When a mechanism generates a wave, that mechanism usually determines the frequency of the wave (e.g. frequency with which the hand in Figure \(\PageIndex{7}\) moves up and down), the speed is determined by the medium, and the wavelength can be determined from Equation 14.1.1.

    Exercise \(\PageIndex{2}\)

    What can you say about the sound emitted by a cello versus that emitted by a violin?

    1. The sound from the violin has a higher frequency.
    2. The sound from the cello has a longer wavelength.
    3. The sound from both instruments propagates at the same speed.
    4. All of the above.
    Answer

    This page titled 14.1: Characteristics of a wave is shared under a CC BY-SA 4.0 license and was authored, remixed, and/or curated by Ryan D. Martin, Emma Neary, Joshua Rinaldo, and Olivia Woodman via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.