14.7: Standing waves
- Page ID
- 19467
As we saw in the last section, when waves have the same frequency, it is possible for them to interfere completely, either destructively or constructively. Waves of the same frequency that interfere can be generated by propagating waves along a string, as the reflected waves from the end of the string will have the same frequency as, and interfere with, the original waves. In general, the resulting wave will be quite complicated, but if you “choose” the frequency (or wavelength) of the generated waves precisely, then the waves will interfere and create a “standing wave”. The standing wave is named this way because it does not appear to propagate along the string. Instead, each point on the string will oscillate with an amplitude that depends on where the point is located along on the string. In contrast, for a traveling wave, all of the points oscillate with the same amplitude.
Three standing waves of different frequencies (wavelengths) are illustrated in Figure \(\PageIndex{1}\).
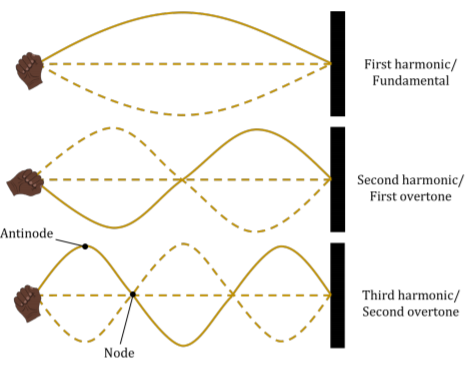
The solid line in each of the three panels corresponds to one particular snapshot of the standing wave at a particular instant in time. The dashed lines correspond to snapshots at different times. In particular, there is a time where the displacement of all points on the string is zero. Each point on the string vibrates with a different amplitude, which corresponds to the solid line (and the opposite dashed line). Certain points do not oscillate at all; these are called “nodes”. The points at the end of the string are always nodes. Certain points vibrate with a maximal amplitude; these are called “anti-nodes”.
In general, if you pluck a taught string (such as a guitar string), you will create a complicated wave, equivalent to many sine waves with different frequencies, that propagate outwards from the point where the string was plucked. Those sine waves will be reflected by the ends of the string and interfere with each other. Most of the waves will interfere in a complicated way and decay away. Those waves that have the correct frequency to create standing waves will persist on the string for a longer period of time. The string will eventually vibrate as a superposition of the fundamental frequency (the standing wave with one anti-node, also called the first harmonic), and the higher “harmonics” (those standing waves with more anti-nodes).
The wavelength of the fundamental standing wave for a string of length, \(L\), is given by the condition:
\[\begin{aligned} \lambda = 2L\end{aligned}\]
In general, the \(n\)th harmonic will have a wavelength of:
\[\lambda_{n}=\frac{2L}{n}\quad n=1,2,3,...,\]
The corresponding frequency is give by:
\[f_{n}=\frac{nv}{2L}\]
where \(v=f\lambda\) is the speed of the waves on the string.
A standing wave is the result of two waves of the same frequency and amplitude traveling in opposite directions. Thus, there is no energy that is transmitted by a standing wave (e.g. through the nodes at the end of the string). Although we described standing waves for a string, these are not restricted to one dimensional waves. For example, the membrane of a drum can also support standing waves.
A standing wave (composed of two travelling waves) has a maximum amplitude \(A\). What must the amplitude \(A_0\) of each travelling wave be?
- \(A_0=1/4 A\)
- \(A_0=1/2 A\)
- \(A_0=A\)
- \(A_0=2A\)
- Answer
In general, most objects can be characterized by a harmonic (or “resonant”) frequency that corresponds to the standing waves that can exist in the object. If that object is, say, shaken, many waves will propagate through the object and cancel out, except those that have the resonant frequency. Relatively small vibrations, if at the correct frequency, can lead to large standing waves that can result in damage to the object.
Mathematical description of a standing wave
A standing wave is the result of two identical waves, traveling in opposite directions, interfering. Consider the waves described by \(D_1(x,t)\) and \(D_2(x,t)\) that are modeled as follows:
\[\begin{aligned} D_1(x,t) &= A\sin(kx-\omega t)\\[4pt] D_2(x,t) &= A\sin(kx+\omega t)\\[4pt]\end{aligned}\]
These two waves are identical, but travel in opposite directions (due to the sign in front of the \(\omega t\)). The superposition of these waves is given by:
\[\begin{aligned} D(x,t) &= D_1(x,t) + D_2(x,t)\\[4pt] &=A\Bigr(\sin(kx-\omega t)+\sin(kx+\omega t)\Bigl)\end{aligned}\]
We can use the following trigonometric identity to combine these into a single term:
\[\begin{aligned} \sin\theta_1+\sin\theta_2 = 2\sin\left(\frac{\theta_1+\theta_2}{2} \right) \cos\left( \frac{\theta_1-\theta_2}{2}\right)\end{aligned}\]
The resulting wave is thus given by:
\[\begin{aligned} D(x,t) &= 2A\sin\left(\frac{kx-\omega t + kx+\omega t}{2} \right) \cos\left( \frac{kx-\omega t - kx-\omega t}{2}\right)\\[4pt] &=2A\sin(kx)\cos(\omega t)\end{aligned}\]
If this wave describes the wave on a string of length \(L\) with both ends held fixed, and we set the origin of our coordinate system at one end of the string, then we require that the displacement at \(x=0\) and \(x=L\) is always zero. The first condition is always true, and the second requires that:
\[\begin{aligned} D(x=L,t) &= 0\\[4pt] \sin(kL) &= 0\\[4pt] \therefore kL &= n\pi \quad\quad n=1,2,3,\dots\end{aligned}\]
and \(kL\) must be a multiple of \(2\pi\). In terms of the wavelength, \(\lambda\), this gives:
\[\begin{aligned} \frac{2\pi}{\lambda}L &= n\pi\\[4pt] \therefore \lambda&= \frac{2L}{n}\end{aligned}\]
as we argued before, for the wavelength of the \(n\)-th harmonic. The standing wave for the \(n\)-th harmonic is thus described by
\[D(x,t)=2A\sin\left(\frac{n\pi}{L}x \right)\cos (\omega t)\]
A point at position \(x\) will behave like a simple harmonic oscillator and oscillate with an amplitude given by:
\[\begin{aligned} A(x) = 2A\sin\left(\frac{n\pi}{L}x\right)\end{aligned}\]
Each point on the string will vibrate with the same angular frequency, \(\omega\), but with a different amplitude, depending on their position. For the \(n\)-th harmonic, the nodes of the standing wave are located at:
\[\begin{aligned} \sin\left(\frac{n\pi}{L}x\right) &=0\\[4pt] \frac{n\pi}{L}x &= m\pi \quad\quad m=0,1,2,\dots\\[4pt] \therefore x &= m\frac{L}{n} \end{aligned}\]
Thus, for example, the second node (\(m=2\)) of the third harmonic (\(n=3\)), is located at \(x=2L/3\), as can be seen in the bottom panel of Figure \(\PageIndex{1}\). The anti-nodes are located at:
\[\begin{aligned} \frac{n\pi}{L}x &= m\frac{\pi}{2} \quad\quad m=1,3,5,7,\dots\\[4pt] \therefore x&=m\frac{L}{2n}\end{aligned}\]
where, for example, the first anti-node of the first harmonic is located at \(x=L/2\), as can be seen in the top panel of Figure \(\PageIndex{1}\).
A standing wave on a string (fixed at both ends) has a fundamental frequency \(f\). If you quadruple the tension in the string, how can you change the length of the string so that the fundamental frequency remains the same?
- half the length.
- double the length.
- triple the length.
- quadruple the length.
- Answer
Olivia Let’s take another look at the equation for a standing wave. In this section, we saw that the equation for a standing wave is given by:
\[\begin{aligned} D(x,t)=2A\sin(kx)\cos(\omega t)\end{aligned}\]
We can rearrange this equation to get:
\[\begin{aligned} D(x,t)=\underbrace{2A\cos(\omega t)}_{\textrm{amplitude}}\sin(kx)\end{aligned}\]
This looks like the equation for a stationary wave (the displacement is a function of \(x\)) with an amplitude \(2A\cos(\omega t)\). We know that \(\cos(\omega t)\) will give a value that ranges between -1 and 1, so we can just think of \(\cos(\omega t)\) as a scaling term that modifies the amplitude of the wave.
When we look at a standing wave, this is exactly what we see - a wave whose amplitude is always changing but that does not travel one way or the other. Figure \(\PageIndex{2}\) shows a few snapshots of what the wave looks like at different times.
We can see from the equation that the maximum amplitude will be \(2A\). This makes sense when we remember that the standing wave is made of two traveling waves of amplitude \(A\). As these waves move, there will be moments when they completely constructively interfere, which is when the amplitude of the standing wave is maximized. When they completely destructively interfere, the amplitude is zero.