18.8: Sample problems and solutions
- Page ID
- 19502
A long cylinder of radius, \(R\), carries a uniform charge per unit volume density, \(\rho\). If the electric potential at the surface of the cylinder is \(V_S = 100\text{V}\), then what is the electric potential inside and outside of the cylinder as a function of \(r\), the distance from the center of the cylinder?
- Answer
-
To determine the electric potential inside and outside of the cylinder, we can use the electric field, which we must first determine. We will do this using Gauss’ Law. We will use a gaussian surface that is a cylinder of radius, \(r\), and length, \(L\). In both regions, the flux of the electric field will be given by:
\[\begin{aligned} \int E dA = E 2\pi rL\end{aligned}\]
since the electric field points in the radial direction, away from the center of the cylinder. Outside of the cylinder (\(r>R\)), the total charge enclosed is the total charge on a length, \(L\), of the cylinder, which has a volume, \(\pi R^2 L\):
\[\begin{aligned} Q^{enc}=\rho \pi R^2 L\end{aligned}\]
Thus, applying Gauss’ Law outside the cylinder, gives the electric field for \(r>R\):
\[\begin{aligned} \int E dA &= \frac{Q_{enc}}{\epsilon_0}\\[4pt] E 2\pi rL &= \frac{\rho \pi R^2 L}{\epsilon_0}\\[4pt] \therefore E(r) &= \frac{\rho R^2}{2\epsilon_0r}\quad(r\geq R)\end{aligned}\]
Inside the cylinder, the enclosed charge is that enclosed by a cylinder of radius, \(r\), and length, \(L\):
\[\begin{aligned} Q^{enc}=\rho \pi r^2 L\end{aligned}\]
Applying Gauss’ Law, the electric field inside the cylinder is given by:
\[\begin{aligned} \int E dA &= \frac{Q_{enc}}{\epsilon_0}\\[4pt] E 2\pi rL &= \frac{\rho \pi r^2 L}{\epsilon_0}\\[4pt] \therefore E(r) &= \frac{\rho r}{2\epsilon_0}\quad(r<R)\end{aligned}\]
Given the electric field everywhere in space, we can now determine the electric potential. We will begin by calculating the electric potential anywhere in the cylinder, \(V(r)\), using the potential difference between that point and the surface of the cylinder:
\[\begin{aligned} \Delta V &= V_S - V(r) = -\int_{r}^{R} \vec E\cdot d \vec r\\[4pt] &= -\int_{r}^{R} \frac{\rho r}{2\epsilon_0} \hat r \cdot d \vec r\\[4pt] &= -\int_{r}^{R} \frac{\rho r}{2\epsilon_0} dr\\[4pt] &= -\frac{\rho (R^2-r^2)}{4\epsilon_0}\\[4pt] \therefore V(r) &= V_S + \frac{\rho (R^2-r^2)}{4\epsilon_0}\\[4pt] &=100\text{V}+\frac{\rho (R^2-r^2)}{4\epsilon_0}\end{aligned}\]
Thus, everywhere inside the cylinder, the electric potential is larger than \(100\text{V}\), since \(R^2-r^2>0\). This makes sense, as the electric field points away from the center, and positive charges will decrease their potential energy by moving further from the center.
We proceed in the same way to determine the difference in potential between a point at a distance, \(r>R\), and the potential, \(V_S\), at the surface of the cylinder:
\[\begin{aligned} \Delta V &= V(r) - V_S = -\int_{R}^{r} \vec E\cdot d \vec r\\[4pt] &= -\int_{R}^{r} \frac{\rho R^2}{2\epsilon_0r} \hat r \cdot d \vec r\\[4pt] &= - \frac{\rho R^2}{2\epsilon_0} \int_{R}^{r} \frac{1}{r}dr\\[4pt] &=- \frac{\rho R^2}{2\epsilon_0} \ln \left( \frac{R}{r} \right)\\[4pt] \therefore V(r) &= V_S - \frac{\rho R^2}{2\epsilon_0} \ln \left( \frac{R}{r} \right)\\[4pt] &= 100\text{V} - \frac{\rho R^2}{2\epsilon_0} \ln \left( \frac{R}{r} \right)\end{aligned}\]
We find that, outside the cylinder, the electric potential decreases from \(100\text{V}\) as one moves away from the cylinder, as expected.
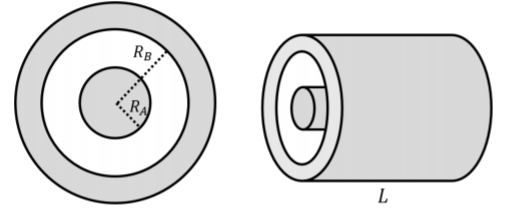
A capacitor is constructed by placing a concentric conducting cylindrical shell of negligible thickness and inner radius, \(R_B\), around a solid conducting cylinder of radius, \(R_A\), as illustrated in Figure \(\PageIndex{1}\). What is the capacitance of this capacitor, where the solid cylinder and the cylindrical shell form the two electrodes?
- Answer
-
We will determine the capacitance by relating the potential difference between the electrodes to the charge stored on the electrodes. By using Gauss’ Law, we can determine the electric field between the electrodes based on the charge on those electrodes, and from there, we can determine the potential difference. We will ignore the fact that the cylinder has a finite length and that Gauss’ Law will not hold near the edges of the cylinder, where the electric field is no longer exactly in the radial direction.
We assume that each electrode carries an equal and opposite charge per unit length, \(\lambda\). In order to determine the electric field in the region \(R_A<r<R_B\), we consider a gaussian surface that is a cylinder of radius, \(r\), and length, \(L\), as illustrated in Figure \(\PageIndex{2}\), which will enclose a charge \(Q^{enc}=\lambda L\) from the inner cylinder.
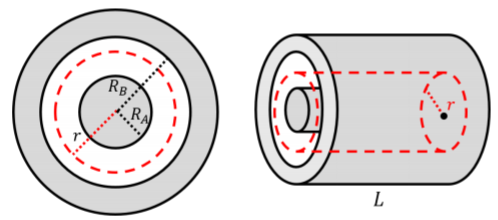
Figure \(\PageIndex{2}\): Solving for \(E\) between two cylinders using Gauss' Law.
Applying Gauss’ Law:
\[\begin{aligned} \int E dA &= \frac{Q_{enc}}{\epsilon_0}\\[4pt] E 2\pi rL &= \frac{\lambda L}{\epsilon_0}\\[4pt] \therefore E(r) &= \frac{\lambda }{2\pi \epsilon_0 r}\end{aligned}\]
and the electric field points in the radial direction (outwards if the inner electrode is positive). We can find the potential difference between the two electrodes using the electric field:
\[\begin{aligned} \Delta V &= V(R_B)-V(R_A)= -\int_{R_A}^{R_B} \vec E \cdot d\vec r\\[4pt] &=-\int_{R_A}^{R_B} \frac{\lambda }{2\pi \epsilon_0 r} dr\\[4pt] &= -\frac{\lambda }{2\pi \epsilon_0}\ln\left( \frac{R_B}{R_A} \right) \end{aligned}\]
where we should note that the minus sign is ambiguous, as the actual sign of the potential difference will depend on the sign of, \(\lambda\), the charge on the inner cylinder. If the charge on the inner cylinder is positive, the potential difference is negative, indicating that the outer cylinder is at a lower potential than the inner one (which makes sense, as the electric field would point outwards between the two cylinders).
We can determine the capacitance between the electrodes, by taking the absolute value of the potential difference above, and using the fact that the charge, \(Q\), on a length, \(L\), of one electrode is given by \(Q=\lambda L\):
\[\begin{aligned} Q &= C\Delta V\\[4pt] \lambda L &= C\frac{\lambda }{2\pi \epsilon_0}\ln\left( \frac{R_B}{R_A} \right)\\[4pt] \therefore C&=\frac{2\pi \epsilon_0}{L\ln\left( \frac{R_B}{R_A} \right)}\end{aligned}\]
We note that the capacitance does not depend on the (arbitrary) charge per unit length, \(\lambda\) that we placed on the inner cylinder in order to model the capacitor. The capacitance only depends on the geometry of the capacitor, and the material that is used between the plates.

