24.5: Electric and magnetic fields and Special Relativity

Last updated
Save as PDF

Page ID: 19555

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

In this section, we present one more example to show how Special Relativity is connected to electromagnetism. Consider a wire that carries an electric current towards the left, and a positive charge, \(+Q\), located next to the wire, as illustrated in Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\): A stationary positive charge, \(+Q\), near a wire carrying current towards the left. This leads to a magnetic field out of the page at the location of \(Q+\).

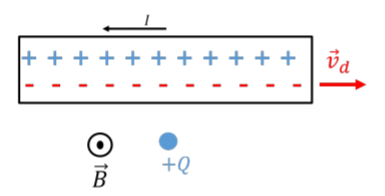
Inside the wire, negative electrons are moving towards the right, with a drift velocity, \(\vec v_d\), while positive ions remain stationary. Since the charge \(+Q\) has a velocity of zero, it experiences no magnetic force. Furthermore, the wire appears to be neutral, with no net electric charge.

If the charge, \(+Q\), has a velocity, \(\vec v_d\), towards the right, it will experience a downwards magnetic force, as illustrated in Figure \(\PageIndex{2}\).

Figure \(\PageIndex{2}\): A positive charge, \(+Q\), moving towards the right, near a wire carrying current towards the left, will experience a downwards magnetic force, \(\vec F_{B} = Q\vec v_{d} × \vec B\).

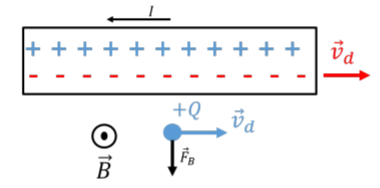
Now, consider this from the perspective of the charge, \(+Q\), as illustrated in Figure \(\PageIndex{3}\). The charge \(Q\) is moving towards the right at the same speed as the electrons in the wire. In the reference frame of the charge, \(+Q\), the charge has a velocity of zero, and thus will experience no magnetic force. The wire still appears to have a (different) current, \(I'\), as the positive ions move to the left, creating a magnetic field, \(\vec B'\), out of the page.

In the “lab” frame of reference, where the electrons and the charge \(+Q\) move towards the right at the same speed, \(v_d\), the electrons appear closer together (length contracted) than they are in the frame of reference of the electrons (or of the charge \(+Q\), since it is moving with the electrons). In the frame of reference of the charge \(+Q\), the electrons thus appear to be spaced further apart (less dense). On the other hand, in the frame of reference of \(+Q\), the positive ions, which are moving towards the left, appear closer together, as the distance between them is now contracted, as illustrated in Figure \(\PageIndex{3}\).

Figure \(\PageIndex{3}\): In the frame of reference of the charge \(+Q\), the charge has a velocity of zero and cannot experience a magnetic force. The ions appear to move to the left, and thus appear denser, since the distance between ions is contracted. The distance between electrons, on the other hand, is larger in this frame of reference. It thus appears that the wire is positively charged, and would exert a downwards electric force on the charge, \(+Q\).

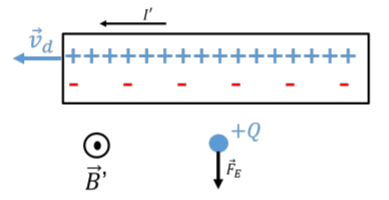
In the frame of reference of the charge \(+Q\), the wire no longer appears neutral, but appears to have a net positive charge. This results in an electric field away from the wire that will exert a downwards force on \(+Q\). In both frames of reference, we conclude that the charge will experience a downwards force. Whether that force is magnetic or electric depends on the frame of reference! Here, we came to the conclusion by using the notion of length contraction, but, remember that it is in fact length contraction that is a consequence of Maxwell’s equations holding in different frames of reference, as we illustrated at the beginning of this chapter.

In most real-world applications, we do not see the effects of Special Relativity, as the speeds involved must be very high for the gamma factor to be appreciably different from 1. However, as you recall, the drift speed of electrons in a wire is usually (much) less than \(\text{mm/s}\), yet, when dealing with the electric and magnetic forces (fields), even the minuscule length contraction of the electrons/ions at those speeds, leads to relativistic effects. This can be thought of in terms of how strong the electric force really is; even a minute change in charge density (due to length contraction) has an appreciable relativistic effect in how we model the dynamics of a charged particle.