25.1: Coordinate Systems
- Page ID
- 19563
Coordinate systems are used to describe the position of an object in space. A coordinate system is an artificial mathematical tool that we construct in order to describe the position of a real object.
1D Coordinate systems
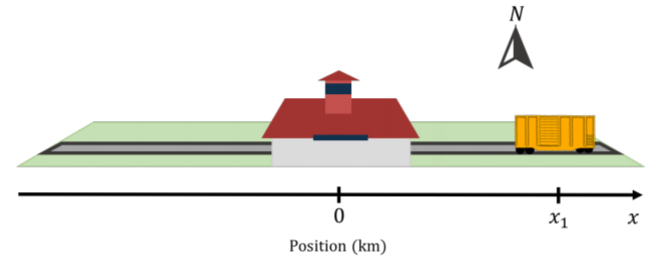
The easiest coordinate system to construct is one that we can use to describe the location of objects in one dimensional space. For example, we may wish to describe the location of a train along a straight section of track that runs in the East-West direction. In order to do so, we must first define an “origin”, which is the reference point of our coordinate system. For example, the origin for our train track may be the Kingston train station (Figure A1.1.1).
We can describe the position of the train by specifying how far it is from the train station (the origin), using a single real number, say \(x\). If the train is at position \(x=0\), then we know that it is at the Kingston station. If the object is not at the origin, then we need to be able to specify on which side (East or West in our train example) of the origin the object is located. We do this by choosing a direction for our one dimensional coordinate \(x\). For example, we may choose that the East side of the track corresponds to positive values of \(x\) and that the West side of the track correspond to the negative values of \(x\). Thus, in order to fully specify a one-dimensional coordinate system we need to choose:
- the location of the origin.
- the direction in which the coordinate, \(x\), increases.
- the units in which we wish to express \(x\).
In one dimension, it is common to use the variable \(x\) to define the position along the “\(x\)-axis”. The \(x\)-axis is our coordinate system in one dimension, and we represent it by drawing a line with an arrow in the direction of increasing \(x\) and indicate where the origin is located (as in Figure A1.1.1).
2D Coordinate systems
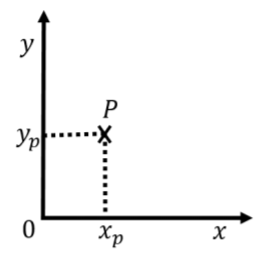
To describe the position of an object in two dimensions (e.g. a marble rolling on a table), we need to specify two numbers. The easiest way to do this is to define two axes, \(x\) and \(y\), whose origin and direction we must define. Figure A1.1.2 shows an example of such a coordinate system. Although it is not necessary to do so, we chose \(x\) and \(y\) axes that are perpendicular to each other. The origin of the coordinate system is where the two axes intersect. One is free to choose any two directions for the axes (as long as they are not parallel). However, choosing axes that are perpendicular (a “Cartesian” coordinate system) is usually the most convenient.
To fully describe the position of an object, we must specify both its position along the \(x\) and \(y\) axes. For example, point \(P\) in Figure A1.1.2 has two coordinates, \(x_p\) and \(y_p\), that define its position. The \(x\) coordinate is found by drawing a line through \(P\) that is parallel to the \(y\) axis and is given by the intersection of that line with the \(x\) axis. The \(y\) coordinate is found by drawing a line through point \(P\) that is parallel to the \(x\) axis and is given by the intersection of that line with the \(y\) axis.
Figure A1.1.3 shows a coordinate system that is not orthogonal (where the \(x\) and \(y\) axes are not perpendicular). Which value on the figure correctly indicates the \(y\) coordinate of point \(P\)?
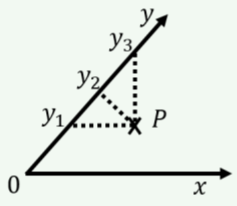
- \(y_1\)
- \(y_2\)
- \(y_3\)
- Answer
-
Add texts here. Do not delete this text first.
The most common choice of coordinate system in two dimensions is the Cartesian coordinate system that we just described, where the \(x\) and \(y\) axes are perpendicular and share a common origin, as shown in Figure A1.1.2. When applicable, by convention, we usually choose the \(y\) axis to correspond to the vertical direction.
Another common choice is a “polar” coordinate system, where the position of an object is specified by a distance to the origin, \(r\), and an angle, \(\theta\), relative to a specified direction, as shown in Figure A1.1.4. Often, a polar coordinate system is defined alongside a Cartesian system, so that \(r\) is the distance to the origin of the Cartesian system and \(\theta\) is the angle with respect to the \(x\) axis.
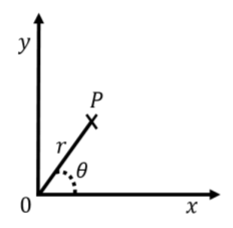
One can easily convert between the two Cartesian coordinates, \(x\) and \(y\), and the two corresponding polar coordinates, \(r\) and \(\theta\):
\[\begin{aligned} x&=r\cos(\theta)\\[4pt] y&=r\sin(\theta)\\[4pt] r&=\sqrt{x^2+y^2}\\[4pt] \tan(\theta) &= \frac{y}{x}\end{aligned}\]
Polar coordinates are often used to describe the motion of an object moving around a circle, as this means that only one of the coordinates (\(\theta\)) changes with time (if the origin of the coordinate system is chosen to coincide with the center of the circle).
3D Coordinate systems
In three dimensions, we need to specify three numbers to describe the position of an object (e.g. a bird flying in the air). In a three dimensional Cartesian coordinate system, we simply add a third axis, \(z\), that is mutually perpendicular to both \(x\) and \(y\). The position of an object can then be specified by using the three coordinates, \(x\), \(y\), and \(z\). By convention, we use the \(z\) axis to be the vertical direction in three dimensions.
Two additional coordinate systems are common in three dimensions: “cylindrical” and “spherical” coordinates. All three systems are illustrated in Figure A1.1.5 superimposed onto the Cartesian system.
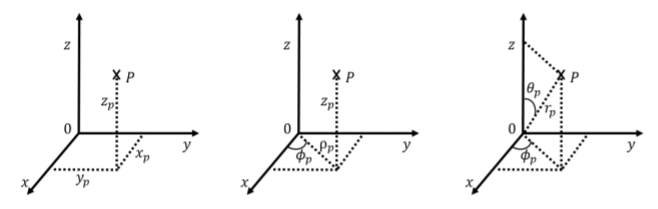
Cylindrical coordinates can be thought of as an extension of the polar coordinates. We keep the same Cartesian coordinate \(z\) to indicate the height above the \(xy\) plane, however, we use the azimuthal angle, \(\phi\), and the radius, \(\rho\), to describe the position of the projection of a point onto the \(xy\) plane. \(\phi\) is the angle between the \(x\) axis and the line from the origin to the projection of the point in the \(xy\) plane and \(\rho\) is the distance between the point and the \(z\) axis. Thus, cylindrical coordinates are very similar to the polar coordinate system introduced in two dimensions, except with the addition of the \(z\) coordinate. Cylindrical coordinates are useful for describing situations with azimuthal symmetry, such as the motion along the surface of a cylinder. For example, consider point \(P\) in Figure A1.1.6. Point \(P\) is located a distance \(\rho\) from the \(z\) axis, as it is located on the surface of the cylinder (the circular end of the cylinder has a radius \(\rho\)). Point \(P\) is a height \(z\) above the \(xy\) plane, and a line from the \(z\) axis to point \(P\) makes an angle \(\phi\) with the \(x\) axis.
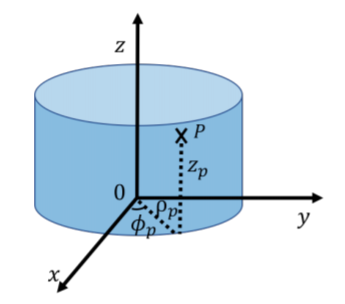
The cylindrical coordinates are related to the Cartesian coordinates by:
\[\begin{aligned} \rho &= \sqrt{x^2+y^2}\\[4pt] \tan(\phi) &= \frac{y}{x}\\[4pt] z&=z\end{aligned}\]
In spherical coordinates, a point \(P\) is described by the radius, \(r\), the polar angle \(\theta\), and the azimuthal angle, \(\phi\). The radius is the distance between the point and the origin. The polar angle is the angle with the \(z\) axis that is made by the line from the origin to the point. The azimuthal angle is defined in the same way as in polar coordinates. Note that the value of \(\phi\) must be between \(0\) and \(2\pi\), whereas the value of \(\theta\) must be between \(0\) and \(\pi\).
Spherical coordinates are useful for describing situations that have spherical symmetry, such as a person walking on the surface of the Earth, since the radial coordinate will not change. For example, this is shown with Point \(P\) in Figure A1.1.7, located on the surface of a sphere of radius \(r\).
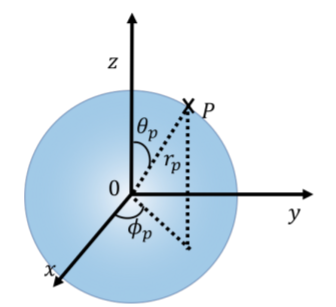
The spherical coordinates are related to the Cartesian coordinates by:
\[\begin{aligned} r &= \sqrt{x^2+y^2+z^2}\\[4pt] \cos(\theta) &= \frac{z}{r}=\frac{z}{\sqrt{x^2+y^2+z^2}}\\[4pt] \tan(\phi) &= \frac{y}{x}\\[4pt]\end{aligned}\]

