28.3: Plotting

Last updated
Save as PDF

Page ID: 19590

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

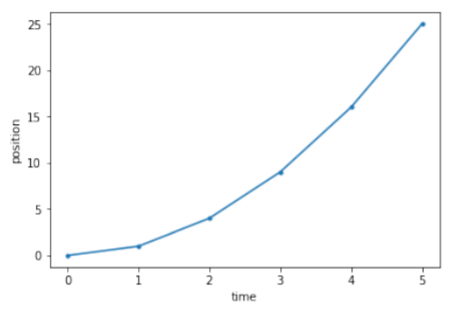
Several modules are available in python for plotting. We will show here how to use the pylab module (which is equivalent to the matplotlib module). For example, we can easily plot the data in the two arrays from the previous section in order to plot the position versus time for the object:

python code \(\PageIndex{1}\)

Plotting two arrays

#import the pylab module
import pylab as pl

#define an array of values for the position of the object
position = [0 ,1 ,4 ,9 ,16 ,25]
#define an array of values for the corresponding times
time = [0 ,1 ,2 ,3 ,4 ,5]

#make the plot showing points and the line (.−)
pl.plot(time, position, '.-')
#add some labels:
pl.xlabel("time") #label for x-axis
pl.ylabel("position") #label for y-axis
#show the plot
pl.show()

Output

Figure A4.3.1: Using two arrays and plotting them.

Exercise \(\PageIndex{1}\)

How would you modify the Python code above to show only the points, and not the line?

Answer

We can use Python to plot any mathematical function that we like. It is important to realize that computers do not have a representation of a continuous function. Thus, if we would like to plot a continuous function, we first need to evaluate that function at many points, and then plot those points. The numpy module provides many useful features for working with arrays of numbers and applying functions directly to those arrays.

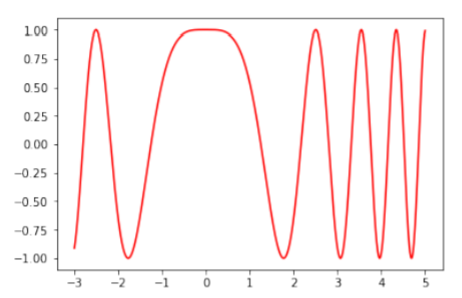
Suppose that we would like to plot the function \(f(x) = cos(x^{2})\) between \(x = −3\) and \(x = 5\). In order to do this in Python, we will first generate an array of many values of \(x\) between \(−3\) and \(5\) using the numpy package and the function linspace(min,max,N) which generates \(N\) linearly spaced points between min and max. We will then evaluate the function at all of those points to create a second array. Finally, we will plot the two arrays against each other:

python code \(\PageIndex{2}\)

Plotting a function of 1 variable

#import the pylab and numpy modules
import pylab as pl
import numpy as np

#Use numpy to generate 1000 values of x between -3 and 5.
#xvals is an array with 1000 values in it:
xvals = np.linspace(-3,5,1000)

#Now, evaluate the function for all of those values of x.
#We use the numpy version of cos, since it allows us to take the cos
#of all values in the array.
#fvals will be an array with the 1000 corresponding cosines of the xvals squared
fvals = np.cos(xvals**2)

#make the plot showing only a line, and color it
pl.plot(xvals, fvals, color='red')
#show the plot
pl.show()

Output

Figure A4.3.2: Plotting a function using arrays.