10.2: Consequences of Einstein's Postulates
- Page ID
- 17425
The combination of the two postulates in section 10.1 leads to a number of consequences that appear to be at odds with everyday experience. They imply that there are no such things as universal measures of time and length, nor even agreement on whether events are simultaneous or not. The reason why we do not observe these consequences all the time is that their effects are very small for objects which are moving slowly (as compared to the speed of light). Nonetheless, they do exist, and can be measured - and matter a lot in situations where speeds are high, such as in particle accelerators and cosmic radiation.
LOSS OF SIMULTANEITY
Consider the following (thought) experiment. Somebody stands in the middle of a train car with mirrors at either end. The car moves with constant speed \(v\) with respect to the platform, at which we place a second observer. The person on the train holds two laser pointers, which she presses at the same time (or perhaps a device with a single button that sends out two beams, to avoid experimenter bias). According to the person on the train, the beams reach both mirrors simultaneously, as they travel at the same speed, and cover the same distance. Now according to the person on the platform, the beams also travel at the same speed(!) - Einstein’s light postulate tells us that all observers measure the speed of light to be the same. However, according to this stationary observer, the train also moves, and thus the light beam traveling to the front of the train has to cover a greater distance than the one going to the back of the train. Consequently, the backwards-traveling beam arrives at its mirror before the forwards-traveling one does. We are forced to conclude that events that are simultaneous in one inertial reference frame are not necessarily simultaneous in another.
Fortunately, there is an event that both observers agree on: the fact that the two light beams, once reflected, return to the person in the middle of the train at the same time. From the point of view of the person on the train this is obvious. For the person on the platform, a simple calculation shows that the distance that the backwards-traveling beam gains on the outbound trip equals the distance it looses on the return trip, and vice versa. Different observers don’t in general agree on the simultaneity (or even order) of events happening at different points in space, but they do agree on the order of events at a given point in space - which means that relativity preserves causality (the concept that causes precede effects).
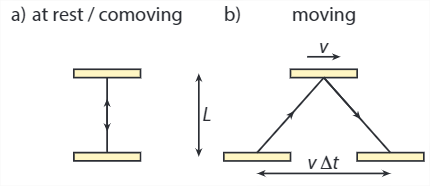
TIME DILATION
Since everybody agrees on the speed of light (and very little else), it makes sense to use the speed of light to determine other physical quantities, such as the time interval between two events. To that end, we can construct a light clock: we place two mirrors in parallel, and let a beam of light bounce back and forth between them (Figure \(\PageIndex{1}\)). Since we agree on at least the order of events at the same point in space, let’s take as our time interval the time it takes for the light to travel back and forth between the mirrors once (i.e., one round trip). According to the comoving observer (whose coordinates we’ll denote with primes, and whose system of coordinates we’ll call \(S'\)), this time interval is given by \(\Delta t' = 2L/c\), as the distance traveled by the light is simply twice the perpendicular distance between the mirrors. However, for the stationary observer it seems that the light has moved in the direction parallel to the mirrors as well (see figure \(\PageIndex(1)\)b). We’ll denote his coordinate system as \(S\), with time interval \(\Delta\). The total distance traveled by the light is (invoking the Pythagorean theorem) \(\sqrt{(2L)^2 + (v\Delta t)^2)}\), which should equal \(c\Delta t\). Solving for \(\Delta t\), we find \( (\Delta t)^2 = (2L)^2/(c^2 -v^2) \), which is longer than the time interval measured by the comoving observer (that makes sense - if the light travels at the same speed, a larger distance should take longer). The two time intervals are related by:
\[ \Delta t = \frac{1}{\sqrt{1-v^2/c^2}}\Delta t' = \gamma (v) \Delta t' \]
The factor \(\gamma (v)\) will return frequently in this chapter. Its value is one if \(v = 0\), and becomes progressively larger as \(v\) increases, to blow up at \(v = c\). For ‘small’ (compared to c) values of \(v\) the value of \(\gamma (v)\) is very close to one, which is why the effects of special relativity hardly ever show up in everyday life.
We have established that time intervals between two events are different for two different (comoving and stationary) observers. There is a subtle but important point to make about how time is perceived to progress according to a single observer. Let’s start out with the stationary observer. Suppose this observer both measures time with a light clock in his own frame of reference, and observes an identical light clock on a moving train. Since the time interval for the roundtrip of the light in the comoving (or in this case, co-stationary) light clock is measured to be less than that of the moving clock, the stationary observer concludes that the moving clock is running slow. This observation is universal, and known as time dilation. To stress how universal time dilation is, consider the point of view of the person on the train: according to her, her clock is running ‘normal’, while the clock on the platform runs slow - which is in perfect agreement with the above statement, as from the point of view of the train, it’s the platform that’s moving.
Michelson-Morley experiment
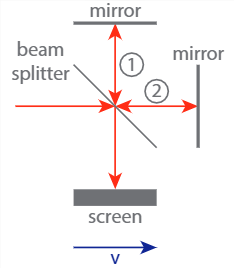
The Michelson-Morley experiment (1887) was an attempt to measure the relative motion of the Earth with respect to the aether, a substance that was postulated to fill all of space. It was well known in the 19th century that the Earth’s atmosphere only extends to about 100 km up, and since sunlight can reach the Earth, it was postulated that there must be another substance that acted as the medium for the propagation of light (much like sound propagates through air, water, or even solids, but not through vacuum). Since the Earth moves around the sun, it should move relatively to the aether, or from the point of view of an observer on Earth, the aether should flow through space (‘aether wind’). Consequently the aether should affect the speed of light for a beam traveling in the same direction as the wind, but not one traveling perpendicular to this direction. Michelson and Morley attempted to use this principle to measure the speed of the aether wind, with a device now known as a Michelson interferometer (pictured). However, they found no difference at all, for any angle of the interferometer arms. Lorentz (see next box) initially attempted to explain this result by introducing the concept of ‘local time’, which would lead to a Lorentz contraction of one of the arms with respect to the other, canceling the effect of the aether wind. Einstein took a more radical approach, dropping the concept of the aether altogether, and replacing it with his two postulates, which have Lorentz contraction as one of their consequences. Three (very sensitive) Michelson interferometers have recently been used to detect small vibrations in spacetime itself, the gravitational waves predicted by Einstein’s general theory of relativity.
If the apparatus moves to the right with speed \(v\), the speed of light on path 1 (up-down) is given by \( u_1 = |\textbf{u}_1| = \sqrt{c^2 - v^2}\). If the distance between the beamsplitter and the mirror is \(L\), the time it takes to traverse path 1 (back and forth) is then given by
\[ t_{1}=\frac{2 L}{u_{1}}=\frac{2 L}{\sqrt{c^{2}-v^{2}}}=\frac{2 L / c}{\sqrt{1-(v / c)^{2}}} .\]
For path 2, the speed of the light on the way out to the mirror equals \( u_{out} = c-v\), while the speed on the return path equals \(u_{in} = c+v\). The total time for the trajectory (also of length \(L\)) thus equals
\[ t_{2}=\frac{L}{c-v}+\frac{L}{c+v}=\frac{2 L / c}{1-(v / c)^{2}}=\frac{1}{\sqrt{1-(v / c)^{2}}} t_{1},\]
so path 2 always takes less time than path 1. (Note that the proportionality factor is exactly the same as the one we’ll find relating the time observed by a comoving and a stationary observer in the relativistic picture - Lorentz wasn’t that far off!). If however the speed of light is identical in paths 1 and 2, the time it takes to traverse either of them is identical too, and we expect no interference.
A rather famous example of the effect of time dilation is the observation of the number of high-velocity muons (particles similar to electrons, but much heavier and unstable) at the surface of the earth. The muons are created in the upper atmosphere (about 20 km up), when cosmic rays collide with atmospheric atoms. The muons have a decay half-time of 2.2 \(\mu\)s (meaning that after this time half of the original muons have decayed). The muons are created at very high speed, close to that of light (\(v = 0.999c\)). Even so, classically they can only travel about 650 m before half of them are gone, and almost none will reach the surface of the earth. However, since according to us stationary observers on earth the muons’ clocks run slow, we expect the half-time to be effectively extended with a factor \(\gamma (0.999c)=22\), resulting in a distance of about 15 km before half of them have decayed, and a significant number reaching the surface - as is observed.
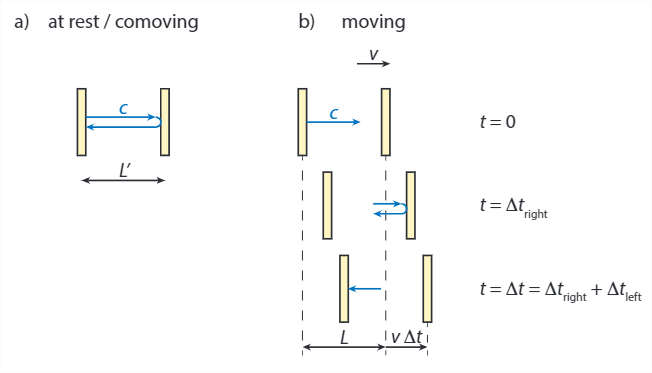
LORENTZ CONTRACTION
Not only do observers in different inertial frames not agree on the duration on time intervals, they do not agree on the length of objects (i.e., the size of space intervals) either. For distances perpendicular to a direction of motion there is no issue - for the light clock in figure \(\PageIndex{1}\), both observers measure a distance \(L\) between the two mirrors. However, if they were to be asked about say the length of the wagon of the train we’re imagining the moving observer to be in, their answers wouldn’t agree.
To see how this difference in measured length comes about and how lengths are related, we return to the light clock, but now turn it on its side (figure \(\PageIndex{3}\))1. For both observers, measuring the distance between the mirrors can be done by measuring the time it takes a lightbeam to make a roundtrip between them. For the comoving observer, we find that \( L' = \frac{1}{2}c\Delta t' \). For the stationary observer, the picture is more complicated, as the mirrors move while the light travels. On the way out, the distance the light has to travel is the distance \(L\) between the mirrors, plus the distance \(v\Delta t_{right}\) the far mirror moves. This total distance should equal \( c\Delta t_{right}\), so we get \( \Delta t_{right} = L/(c-v) \). On the way back, we get a traveled distance of \(L\) minus \( v\Delta t_{left} \), which should equal \(c\Delta t_{left}\), so we get \( \Delta t_{left} = L/(c+v) \). The total time traveled is the sum of these two, which is given by:
\[\Delta t = \Delta t_{right} + \Delta t_{left} = \frac{L}{c-v} + \frac{L}{c+v} = \frac{2Lc}{c^2-v^2}\]
or
\[L=\frac{c^{2}-v^{2}}{2 c} \Delta t=\frac{c^{2}-v^{2}}{2 c} \gamma(v) \Delta t^{\prime}=\frac{c^{2}-v^{2}}{c^{2}} \gamma(v) L^{\prime}=\frac{1}{\gamma(v)} L^{\prime} \label{eq:1}\]
The two lengths are thus related by the inverse of the \(\gamma\) factor that relates two time intervals. Using an argument similar to that of the clocks (relating the length of two identical sticks, one stationary and one moving), we can conclude that moving lengths contract, an effect known as Lorentz contraction. There is an interesting symmetry between time dilation and Lorentz contraction, which gives an alternative way of getting equation (\(\ref{eq:1}\)) once the effect of time dilation is known. Consider again the example of the muons, but now go to the frame co-moving with the muons. In this frame, the decay half-time is still 2.2 \(\mu\)s, but the same number of muons reach the surface of the earth as in the stationary frame. The reason is that according to the muons, the distance from the upper atmosphere to the surface is contracted, by exactly a factor 1/\(\gamma (v)\), which gives the same distance of 15 km at which half of them have decayed.
1 Alternatively, we may say that we measure the length of the train wagon by sending a light beam back and forth in the wagon, bouncing off a mirror at the end.


