18.4: Capacitors and Dielectrics
- Page ID
- 14553
learning objectives
- Express the relationship between the capacitance, charge of an object, and potential difference in the form of equation
Capacitance is the measure of an object’s ability to store electric charge. Any body capable of being charged in any way has a value of capacitance.
The unit of capacitance is known as the Farad (F), which can be adjusted into subunits (the millifarad (mF), for example) for ease of working in practical orders of magnitude. The Farad can be equated to many quotients of units, including JV-2, WsV-2, CV-1, and C2J-1.
The most common capacitor is known as a parallel-plate capacitor which involves two separate conductor plates separated from one another by a dielectric. Capacitance (C) can be calculated as a function of charge an object can store (q) and potential difference (V) between the two plates:
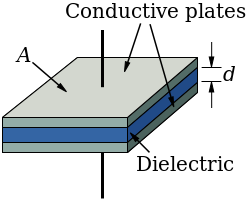
Parallel-Plate Capacitor: The dielectric prevents charge flow from one plate to the other.
\[\mathrm { C } = \dfrac { \mathrm { q } } { \mathrm { V } }\]
Ultimately, in such a capacitor, q depends on the surface area (A) of the conductor plates, while V depends on the distance (d) between the plates and the permittivity (εr) of the dielectric between them. For a parallel-plate capacitor, this equation can be used to calculate capacitance:
\[\mathrm { C } = \epsilon _ { \mathrm { r } } \epsilon _ { 0 } \dfrac { \mathrm { A } } { \mathrm { d } } \]
Where ε0 is the electric constant. The product of length and height of the plates can be substituted in place of A.
In storing charge, capacitors also store potential energy, which is equal to the work (W) required to charge them. For a capacitor with plates holding charges of +q and -q, this can be calculated:
\[\mathrm{W_{charging}=∫^Q_0\dfrac{q}{C}dq=\dfrac{CV^2}{2}=W_{stored}}\]
Thus, either through calculus or algebraically (if C and V are known), stored energy (Wstored) can be calculated. In a parallel-plate capacitor, this can be simplified to:
\[\mathrm { W } _ { \mathrm { stored } } = \dfrac { \epsilon _ { \mathrm { \epsilon } _ { 0 } \mathrm { A } } \mathrm { V } ^ { 2 } } { 2 \mathrm { d } }\]
Capacitors with Dielectrics
A dielectric partially opposes a capacitor’s electric field but can increase capacitance and prevent the capacitor’s plates from touching.
learning objectives
- Describe the behavior of the dielectric material in a capacitor’s electric field
In order for a capacitor to hold charge, there must be an interruption of a circuit between its two sides. This interruption can come in the form of a vacuum (the absence of any matter) or a dielectric (an insulator).
When a dielectric is used, the material between the parallel plates of the capacitor will polarize. The part near the positive end of the capacitor will have an excess of negative charge, and the part near the negative end of the capacitor will have an excess of positive charge. This redistribution of charge in the dielectric will thus create an electric field opposing the field created by the capacitor.
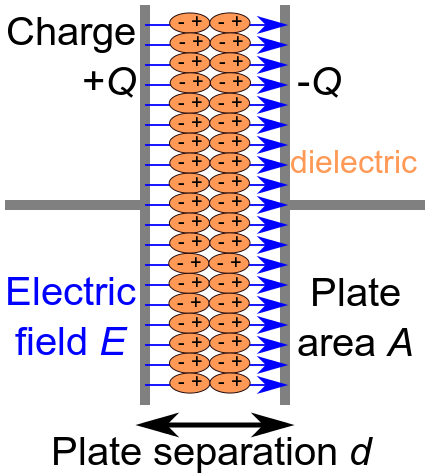
Diagram of a Parallel-Plate Capacitor: Charges in the dielectric material line up to oppose the charges of each plate of the capacitor. An electric field is created between the plates of the capacitor as charge builds on each plate.
Therefore, the net field created by the capacitor will be partially decreased, as will the potential difference across it, by the dielectric. On the other hand, the dielectric prevents the plates of the capacitor from coming into direct contact (which would render the capacitor useless). If it has a high permittivity, it also increases the capacitance for any given voltage. The capacitance for a parallel-plate capacitor is given by:
c=ϵAdc=ϵAd
where ε is the permittivity, A is the area of the capacitor plates (assuming both are the same size and shape), and d is the thickness of the dielectric.
Any insulator can be used as a dielectric, but the materials most commonly used are selected for their ability to resist ionization. The more resistant a material is to ionization, the more tolerance it has for operating at higher voltages. Eventually every material has a “dielectric breakdown point,” at which the potential difference becomes too high for it to insulate, and it ionizes and permits the passage of current.
Parallel-Plate Capacitor
The parallel-plate capacitor is one that includes two conductor plates, each connected to wires, separated from one another by a thin space.
learning objectives
- Calculate the maximum storable energy in a parallel-plate capacitor
One of the most commonly used capacitors in industry and in the academic setting is the parallel-plate capacitor. This is a capacitor that includes two conductor plates, each connected to wires, separated from one another by a thin space. Between them can be a vacuum or a dielectric material, but not a conductor.
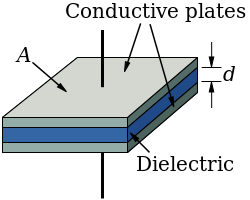
Parallel-Plate Capacitor: In a capacitor, the opposite plates take on opposite charges. The dielectric ensures that the charges are separated and do not transfer from one plate to the other.
The purpose of a capacitor is to store charge, and in a parallel-plate capacitor one plate will take on an excess of positive charge while the other becomes more negative.
Assuming the plates extend uniformly over an area of A and hold ± Q charge, their charge density is ±, where ρ=Q/A. Assuming that the dimensions of length and width for the plates are significantly greater than the distance (d) between them, the electric field (E) near the center of the plates can be calculated by:
\[\mathrm { E } = \dfrac { \rho } { \epsilon }\]
Potential (V) between the plates can be calculated from the line integral of the electric field (E):
\[\mathrm { V } = \int _ { 0 } ^ { \mathrm { d } } \mathrm { Edz }\]
where z is the axis perpendicular to both plates. Through simplification and substitution, this integral can be changed to:
\[\mathrm { V } = \dfrac { \rho \mathrm { d } } { \epsilon } = \dfrac { \mathrm { Qd } } { \epsilon \mathrm { A } }\]
Given that capacitance is the quotient of charge and potential:
\[\mathrm { C } = \dfrac { \epsilon \mathrm { A } } { \mathrm { d } }\]
Accordingly, capacitance is greatest in devices with high permittivity, large plate area, and minimal separation between the plates.
The maximum energy (U) a capacitor can store can be calculated as a function of Ud, the dielectric strength per distance, as well as capacitor’s voltage (V) at its breakdown limit (the maximum voltage before the dielectric ionizes and no longer operates as an insulator):
\[\mathrm { U } = \dfrac { \mathrm { CV } ^ { 2 } } { 2 } = \dfrac { \epsilon \mathrm { A } \left( \mathrm { U } _ { \mathrm { dd } } \right) ^ { 2 } } { 2 \mathrm { d } } = \dfrac { \epsilon \mathrm { AdU } _ { \mathrm { d } } ^ { 2 } } { 2 }\]
Combinations of Capacitors: Series and Parallel
Like any other form of electrical circuitry device, capacitors can be used in series and/or in parallel within circuits.
learning objectives
- Calculate the total capacitance for the capacitors connected in series and in parallel
Like any other form of electrical circuitry device, capacitors can be used in combination in circuits. These combinations can be in series (in which multiple capacitors can be found along the same path of wire) and in parallel (in which multiple capacitors can be found along different paths of wire).
Capacitors in Series
Like in the case of resistors in parallel, the reciprocal of the circuit’s total capacitance is equal to the sum of the reciprocals of the capacitance of each individual capacitor:
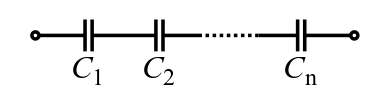
Capacitors in Series: This image depicts capacitors C1, C2 and so on until Cn in a series.
\[\dfrac { 1 } { \mathrm { C } _ { \mathrm { total } } } = \dfrac { 1 } { \mathrm { C } _ { 1 } } + \dfrac { 1 } { \mathrm { C } _ { 2 } } + \ldots + \frac { 1 } { \mathrm { C } _ { \mathrm { n } } }\]
This can also be expressed as:
\[\mathrm { C } _ { \mathrm { total } } = \mathrm{\dfrac { 1 } { \dfrac { 1 } { C _ { 1 } } + \dfrac { 1 } { C _ { 2 } } + \ldots + \dfrac { 1 } { C _ { n } } }}\]
Parallel Capacitors
Total capacitance for a circuit involving several capacitors in parallel (and none in series) can be found by simply summing the individual capacitances of each individual capacitor.
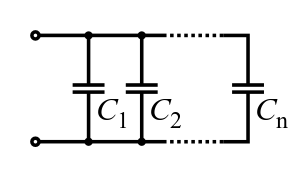
Parallel Capacitors: This image depicts capacitors C1, C2, and so on until Cn in parallel.
\[\mathrm { C } _ { \mathrm { total } } = \mathrm { C } _ { 1 } + \mathrm { C } _ { 2 } + \ldots + \mathrm { C } _ { \mathrm { n } } \]
Capacitors in Series and in Parallel
It is possible for a circuit to contain capacitors that are both in series and in parallel. To find total capacitance of the circuit, simply break it into segments and solve piecewise.
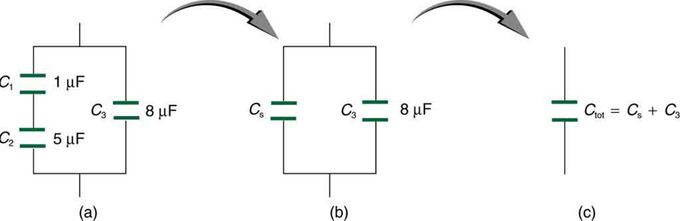
Capacitors in Series and in Parallel: The initial problem can be simplified by finding the capacitance of the series, then using it as part of the parallel calculation.
The circuit shown in (a) contains C1 and C2 in series. However, these are both in parallel with C3. If we find the capacitance for the series including C1 and C2, we can treat that total as that from a single capacitor (b). This value can be calculated as approximately equal to 0.83 μF.
With effectively two capacitors left in parallel, we can add their respective capacitances (c) to find the total capacitance for the circuit. This sum is approximately 8.83 μF.
Dieletrics and their Breakdown
Dielectric breakdown is the phenomenon in which a dielectric loses its ability to insulate, and instead becomes a conductor.
learning objectives
- Identify conditions that can lead to a dielectric breakdown and its effect on materials
Dielectric breakdown (illustrated in ) is the phenomenon in which a dielectric loses its ability to insulate, and instead becomes a conductor. Dielectrics are commonly used either to isolate conductors from a variable external environment (e.g., as coating for electrical wires) or to isolate conductors from one another (e.g., between plates of a parallel-plate capacitor). In all applications, they are selected for their ability to act as insulators. By definition, an insulator is unable to conduct electricity. Under certain conditions, however, a material that is an insulator can become a conductor.
Eventually, exposing any insulator to increasing voltage will result in the insulator becoming conductive. This point (the minimum voltage for the insulator to become a conductor) is known as the breakdown voltage. Breakdown is more of a rough concept than an exact science. A material’s breakdown voltage cannot be precisely defined. As a failure, there is a probabilistic element and thus a dielectric may experience a breakdown at any of a range of voltages. Additionally, the nature of the voltage used to induce breakdown must be considered. Short pulses can be used in stress testing to resemble lightning strikes, as could a continuous applied voltage.
However, for the case of a gas being used as a dielectric, the following equation has been proven to be rather reliable in predicting breakdown voltage (Vb):
\[\mathrm { V } _ { \mathrm { b } } = \dfrac { \mathrm { Bpd } } { \ln \mathrm { Apd } - \ln \left( \ln \left( 1 + \frac { 1 } { \gamma _ { \mathrm { se } } } \right) \right) }\]
where A and B are constants that depend on the surrounding gas, p is the pressure of the surrounding gas, d is distance between the electrodes (in cm) and γse is the secondary electron emission coefficient. Gaseous dielectrics commonly experience breakdown in nature (the phenomenon of lightning is the most common example).

Dielectric breakdown of plexiglas: The treelike pattern in the plexiglas stems from the root of the breakdown. Current is dispersed in many different directions, creating different stems.
Key Points
- The unit of capacitance is known as the farad (F), which can be equated to many quotients of units, including JV-2, WsV-2, CV-1, and C2J-1.
- Capacitance (C) can be calculated as a function of charge an object can store (q) and potential difference (V) between the two plates: \(\mathrm { C } = \frac { \mathrm { q } } { \mathrm { V } } \). Q depends on the surface area of the conductor plates, while V depends on the distance between the plates and the permittivity of the dielectric between them.
- In storing charge, capacitors also store potential energy, which is equal to the work (W) required to charge them. For a capacitor with plates holding charges of +q and -q, this can be calculated: \(\mathrm { W } _ { \mathrm { stored } } = \frac { \mathrm { CV } ^ { 2 } } { 2 }\). The above can be equated with the work required to charge the capacitor.
- When a dielectric is used, the material between the plates will polarize to oppose the dielectric’s field. The net field created by the capacitor will be partially decreased, as will the potential difference across it, by the dielectric.
- Capacitance for a parallel -plate capacitor is given by: \(\mathbf { c } = \frac { \epsilon \mathrm { A } } { \mathrm { d } } \) where ε is the permittivity, A is the area of the capacitor plates (assuming both are the same size and shape), and d is the thickness of the dielectric.
- Any insulator can be used as a dielectric, but the materials most commonly used are selected for their ability to resist ionization. The more resistant a material is to ionization, the more tolerance it has for operating at higher voltages.
- Assuming the plates extend uniformly over an area of A and hold ± Q charge, their charge density is ±, where ρ=Q/A.
- Assuming that the dimensions of length and width for the plates are significantly greater than the distance (d) between them, \(\mathrm { E } = \frac { \rho } { \epsilon }\) can be used to calculate the electric field (E) near the center of the plates. In this equation, ε represents permittivity.
- \(\mathbf { V } = \frac { \rho \mathrm { d } } { \epsilon } = \frac { \mathrm { Q } \mathrm { d } } { \epsilon \mathrm { A } }\) can be used to calculate the potential between the plates.
- \(\mathrm { C } = \frac { \epsilon \mathrm { A } } { \mathrm { d } }\) can be found from the previous equation, adjusting the terms to solve for capacitance (C).
- \(\mathrm { U } = \frac { \mathrm { CV } ^ { 2 } } { 2 } = \frac { \epsilon \mathrm { A } \left( \mathrm { U } _ { \mathrm { dd } } \right) ^ { 2 } } { 2 \mathrm { d } } = \frac { \epsilon \mathrm { A } \mathrm { d } \mathrm { U } _ { \mathrm { d } } ^ { 2 } } { 2 } \) solves for the maximum storable energy in a parallel-plate capacitor (U) as a function of Ud, the dielectric strength per distance as well as capacitor’s voltage (V) at its breakdown limit.
- \(\frac { 1 } {\mathrm{C} _ { \mathrm { total } } } = \frac { 1 } { \mathrm { C } _ { 1 } } + \frac { 1 } { \mathrm { C } _ { 2 } } + \ldots + \frac { 1 } { \mathrm { C } _ { \mathrm { n } } }\) Capacitors in series follow the law of reciprocals; the reciprocal of the circuit ‘s total capacitance is equal to the sum of the reciprocals of the capacitances of each individual capacitor.
- \(\mathrm { C } _ { \mathrm { total } } = \mathrm { C } _ { 1 } + \mathrm { C } _ { 2 } + \ldots + \mathrm { C } _ { \mathrm { n } }\) For capacitors in parallel, summing the capacitances of individual capacitors affords the total capacitance in the circuit.
- When capacitors are found both in series and in parallel in the same circuit, it is best to simplify the circuit by solving parts of it in sequence.
- All insulators can, when exposed to enough voltage, experience dielectric breakdown and become conductors.
- Because dielectric breakdown is a failure that depends on a probability, an exact breakdown voltage is in most cases impossible to calculate with a high degree of certainty.
- Lightning is a common instance of dielectric breakdown, as air loses its ability to separate the potential difference between clouds and the point of a lightning bolt’s impact.
Key Terms
- dielectric: An electrically insulating or nonconducting material considered for its electric susceptibility (i.e., its property of polarization when exposed to an external electric field).
- capacitance: The property of an electric circuit or its element that permits it to store charge, defined as the ratio of stored charge to potential over that element or circuit (Q/V); SI unit: farad (F).
- capacitor: An electronic component capable of storing an electric charge, especially one consisting of two conductors separated by a dielectric.
- permittivity: A property of a dielectric medium that determines the forces that electric charges placed in the medium exert on each other.
- circuit: A pathway of electric current composed of individual electronic components, such as resistors, transistors, capacitors, inductors and diodes, connected by conductive wires or traces through which electric current can flow. T
- conductor: A material which contains movable electric charges.
- breakdown: A failure, particularly mechanical; something that has failed.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- Capacitance. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Capacitance. License: CC BY-SA: Attribution-ShareAlike
- dielectric. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/dielectric. License: CC BY-SA: Attribution-ShareAlike
- capacitance. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/capacitance. License: CC BY-SA: Attribution-ShareAlike
- Parallel plate capacitor. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Parallel_plate_capacitor.svg. License: CC BY-SA: Attribution-ShareAlike
- Dielectric. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Dielectric. License: CC BY-SA: Attribution-ShareAlike
- capacitor. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/capacitor. License: CC BY-SA: Attribution-ShareAlike
- dielectric. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/dielectric. License: CC BY-SA: Attribution-ShareAlike
- capacitance. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/capacitance. License: CC BY-SA: Attribution-ShareAlike
- Parallel plate capacitor. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Parallel_plate_capacitor.svg. License: CC BY-SA: Attribution-ShareAlike
- Capacitor schematic with dielectric. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Capacitor_schematic_with_dielectric.svg. License: CC BY-SA: Attribution-ShareAlike
- Capacitor. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Capacitor. License: CC BY-SA: Attribution-ShareAlike
- capacitor. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/capacitor. License: CC BY-SA: Attribution-ShareAlike
- dielectric. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/dielectric. License: CC BY-SA: Attribution-ShareAlike
- permittivity. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/permittivity. License: CC BY-SA: Attribution-ShareAlike
- Parallel plate capacitor. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Parallel_plate_capacitor.svg. License: CC BY-SA: Attribution-ShareAlike
- Capacitor schematic with dielectric. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Capacitor_schematic_with_dielectric.svg. License: CC BY-SA: Attribution-ShareAlike
- Parallel plate capacitor. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Parallel_plate_capacitor.svg. License: CC BY-SA: Attribution-ShareAlike
- Series and parallel circuits. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Series_and_parallel_circuits. License: CC BY-SA: Attribution-ShareAlike
- capacitor. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/capacitor. License: CC BY-SA: Attribution-ShareAlike
- circuit. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/circuit. License: CC BY-SA: Attribution-ShareAlike
- Parallel plate capacitor. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Parallel_plate_capacitor.svg. License: CC BY-SA: Attribution-ShareAlike
- Capacitor schematic with dielectric. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Capacitor_schematic_with_dielectric.svg. License: CC BY-SA: Attribution-ShareAlike
- Parallel plate capacitor. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Parallel_plate_capacitor.svg. License: CC BY-SA: Attribution-ShareAlike
- Capacitors in parallel. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Capacitors_in_parallel.svg. License: CC BY-SA: Attribution-ShareAlike
- Capacitors in series. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Capacitors_in_series.svg. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Capacitors in Series and Parallel. January 7, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42336/latest/. License: CC BY: Attribution
- Breakdown voltage. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Breakdown_voltage. License: CC BY-SA: Attribution-ShareAlike
- Electrical breakdown. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Electrical_breakdown. License: CC BY-SA: Attribution-ShareAlike
- breakdown. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/breakdown. License: CC BY-SA: Attribution-ShareAlike
- dielectric. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/dielectric. License: CC BY-SA: Attribution-ShareAlike
- conductor. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/conductor. License: CC BY-SA: Attribution-ShareAlike
- Parallel plate capacitor. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Parallel_plate_capacitor.svg. License: CC BY-SA: Attribution-ShareAlike
- Capacitor schematic with dielectric. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Capacitor_schematic_with_dielectric.svg. License: CC BY-SA: Attribution-ShareAlike
- Parallel plate capacitor. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Parallel_plate_capacitor.svg. License: CC BY-SA: Attribution-ShareAlike
- Capacitors in parallel. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Capacitors_in_parallel.svg. License: CC BY-SA: Attribution-ShareAlike
- Capacitors in series. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Capacitors_in_series.svg. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Capacitors in Series and Parallel. January 7, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42336/latest/. License: CC BY: Attribution
- Square1. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Square1.jpg. License: CC BY-SA: Attribution-ShareAlike


