2.4: Heat Capacity and Equipartition of Energy
- Page ID
- 4353
By the end of this section, you will be able to:
- Solve problems involving heat transfer to and from ideal monatomic gases whose volumes are held constant
- Solve similar problems for non-monatomic ideal gases based on the number of degrees of freedom of a molecule
- Estimate the heat capacities of metals using a model based on degrees of freedom
In the chapter on temperature and heat, we defined the specific heat capacity with the equation \(Q = mc\Delta T\), or \(c = (1/m)Q/\Delta T\). However, the properties of an ideal gas depend directly on the number of moles in a sample, so here we define specific heat capacity in terms of the number of moles, not the mass. Furthermore, when talking about solids and liquids, we ignored any changes in volume and pressure with changes in temperature—a good approximation for solids and liquids, but for gases, we have to make some condition on volume or pressure changes. Here, we focus on the heat capacity with the volume held constant. We can calculate it for an ideal gas.
Heat Capacity of an Ideal Monatomic Gas at Constant Volume
We define the molar heat capacity at constant volume \(C_V\) as
\[\underbrace{C_V = \dfrac{1}{n} \dfrac{Q}{\Delta T}}_{\text{with constant V}}\nonumber \]
This is often expressed in the form
\[Q = nC_V\Delta T\nonumber \]
If the volume does not change, there is no overall displacement, so no work is done, and the only change in internal energy is due to the heat flow \(\Delta E_{int} = Q\). (This statement is discussed further in the next chapter.) We use the equation \(E_{int} = 3nRT/2\) to write \(\Delta E_{int} = 3nR\Delta T/2\) and substitute \(\Delta E\) for Q to find \(Q = 3nR\Delta T/2\), which gives the following simple result for an ideal monatomic gas:
\[C_V = \dfrac{3}{2}R.\nonumber \]
It is independent of temperature, which justifies our use of finite differences instead of a derivative. This formula agrees well with experimental results.
In the next chapter we discuss the molar specific heat at constant pressure \(C_p\), which is always greater than \(C_V\).
A sample of 0.125 kg of xenon is contained in a rigid metal cylinder, big enough that the xenon can be modeled as an ideal gas, at a temperature of \(20.0^oC\). The cylinder is moved outside on a hot summer day. As the xenon comes into equilibrium by reaching the temperature of its surroundings, 180 J of heat are conducted to it through the cylinder walls. What is the equilibrium temperature? Ignore the expansion of the metal cylinder.
Solution
- Identify the knowns: We know the initial temperature \(T_1\) is \(20.0^oC\), the heat Q is 180 J, and the mass m of the xenon is 0.125 kg.
- Identify the unknown. We need the final temperature, so we’ll need \(\Delta T\).
- Determine which equations are needed. Because xenon gas is monatomic, we can use \(Q = 3nR\Delta T/2\). Then we need the number of moles \(n = m/M\).
- Substitute the known values into the equations and solve for the unknowns.
The molar mass of xenon is 131.3 g, so we obtain
\[n = \dfrac{125 \, g}{131.3 \, g/mol} = 0.952 \, mol, \nonumber\nonumber \]
\[\Delta T = \dfrac{2Q}{3nR} = \dfrac{2(180 \, J)}{3(0.952 \, mol)(8.31 \, J/mol \cdot \, ^oC)} = 15.2^oC. \nonumber\nonumber \]
Therefore, the final temperature is \(35.2^oC \). The problem could equally well be solved in kelvin; as a kelvin is the same size as a degree Celsius of temperature change, you would get \(\Delta T = 15.2 \, K \).
Significance
The heating of an ideal or almost ideal gas at constant volume is important in car engines and many other practical systems.
Suppose 2 moles of helium gas at 200 K are mixed with 2 moles of krypton gas at 400 K in a calorimeter. What is the final temperature?
- Answer
-
As the number of moles is equal and we know the molar heat capacities of the two gases are equal, the temperature is halfway between the initial temperatures, 300 K.
We would like to generalize our results to ideal gases with more than one atom per molecule. In such systems, the molecules can have other forms of energy beside translational kinetic energy, such as rotational kinetic energy and vibrational kinetic and potential energies. We will see that a simple rule lets us determine the average energies present in these forms and solve problems in much the same way as we have for monatomic gases.
Degrees of Freedom
In the previous section, we found that \(\frac{1}{2}mv^2 = \frac{3}{2}k_BT\) and \(v^2 = 3v_x^2\), from which it follows that \(\frac{1}{2}mv_x^2 = \frac{1}{2}k_BT\). The same equation holds for \(\frac{3}{2}k_BT\) as the sum of contributions of \(\frac{1}{2}k_BT\) from each of the three dimensions of translational motion. Shifting to the gas as a whole, we see that the 3 in the formula \(C_V = \frac{3}{2}R\) also reflects those three dimensions. We define a degree of freedom as an independent possible motion of a molecule, such as each of the three dimensions of translation. Then, letting d represent the number of degrees of freedom, the molar heat capacity at constant volume of a monatomic ideal gas is \(C_V = \frac{d}{2}R\), where \(d = 3\).
The branch of physics called statistical mechanics tells us, and experiment confirms, that \(C_V\) of any ideal gas is given by this equation, regardless of the number of degrees of freedom. This fact follows from a more general result, the equipartition theorem, which holds in classical (non-quantum) thermodynamics for systems in thermal equilibrium under technical conditions that are beyond our scope. Here, we mention only that in a system, the energy is shared among the degrees of freedom by collisions.
The energy of a thermodynamic system in equilibrium is partitioned equally among its degrees of freedom. Accordingly, the molar heat capacity of an ideal gas is proportional to its number of degrees of freedom, d: \[C_V = \dfrac{d}{2}R.\nonumber \]
This result is due to the Scottish physicist James Clerk Maxwell (1831−1871), whose name will appear several more times in this book.
For example, consider a diatomic ideal gas (a good model for nitrogen, \(N_2\), and oxygen, \(O_2\)). Such a gas has more degrees of freedom than a monatomic gas. In addition to the three degrees of freedom for translation, it has two degrees of freedom for rotation perpendicular to its axis. Furthermore, the molecule can vibrate along its axis. This motion is often modeled by imagining a spring connecting the two atoms, and we know from simple harmonic motion that such motion has both kinetic and potential energy. Each of these forms of energy corresponds to a degree of freedom, giving two more.
We might expect that for a diatomic gas, we should use 7 as the number of degrees of freedom; classically, if the molecules of a gas had only translational kinetic energy, collisions between molecules would soon make them rotate and vibrate. However, as explained in the previous module, quantum mechanics controls which degrees of freedom are active. The result is shown in Figure \(\PageIndex{1}\). Both rotational and vibrational energies are limited to discrete values. For temperatures below about 60 K, the energies of hydrogen molecules are too low for a collision to bring the rotational state or vibrational state of a molecule from the lowest energy to the second lowest, so the only form of energy is translational kinetic energy, and \(d = 3\) or \(C_V = 3R/2\) as in a monatomic gas. Above that temperature, the two rotational degrees of freedom begin to contribute, that is, some molecules are excited to the rotational state with the second-lowest energy. (This temperature is much lower than that where rotations of monatomic gases contribute, because diatomic molecules have much higher rotational inertias and hence much lower rotational energies.) From about room temperature (a bit less than 300 K) to about 600 K, the rotational degrees of freedom are fully active, but the vibrational ones are not, and \(d = 5\). Then, finally, above about 3000 K, the vibrational degrees of freedom are fully active, and \(d = 7\) as the classical theory predicted.
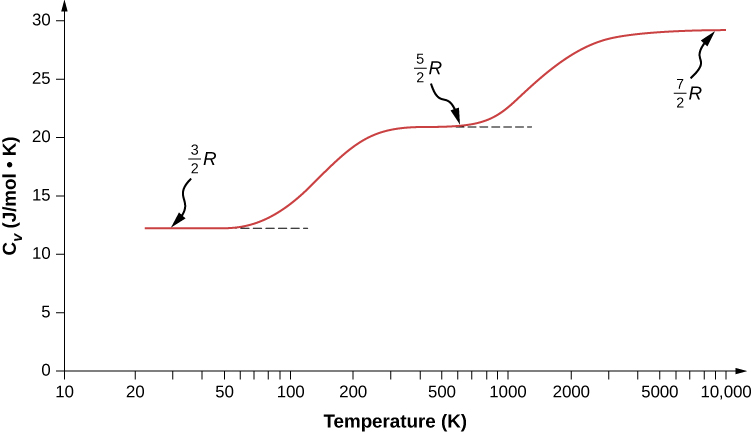
Polyatomic molecules typically have one additional rotational degree of freedom at room temperature, since they have comparable moments of inertia around any axis. Thus, at room temperature, they have \(d = 6\) and at high temperature, \(d = 8\). We usually assume that gases have the theoretical room-temperature values of d.
As shown in Table \(\PageIndex{1}\), the results agree well with experiments for many monatomic and diatomic gases, but the agreement for triatomic gases is only fair. The differences arise from interactions that we have ignored between and within molecules.
| Gas | \(C_V/R\) at \(25^oC\) and 1 atm |
|---|---|
| Ar | 1.50 |
| He | 1.50 |
| Ne | 1.50 |
| CO | 2.50 |
| \(H_2\) | 2.47 |
| \(N_2\) | 2.50 |
| \(O_2\) | 2.53 |
| \(F_2\) | 2.8 |
| \(CO_2\) | 3.48 |
| \(H_2S\) | 3.13 |
| \(N_2O\) | 3.66 |
What about internal energy for diatomic and polyatomic gases? For such gases, \(C_V\) is a function of temperature (Figure \(\PageIndex{1}\)), so we do not have the kind of simple result we have for monatomic ideal gases.
Molar Heat Capacity of Solid Elements
The idea of equipartition leads to an estimate of the molar heat capacity of solid elements at ordinary temperatures. We can model the atoms of a solid as attached to neighboring atoms by springs (Figure \(\PageIndex{2}\)).
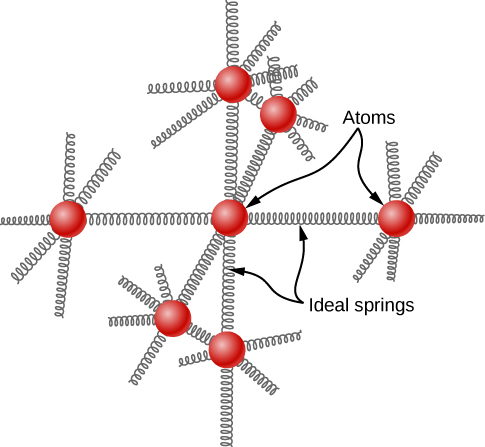
Analogously to the discussion of vibration in the previous module, each atom has six degrees of freedom: one kinetic and one potential for each of the x-, y-, and z-directions. Accordingly, the molar specific heat of a metal should be 3R. This result, known as the Law of Dulong and Petit, works fairly well experimentally at room temperature. (For every element, it fails at low temperatures for quantum-mechanical reasons. Since quantum effects are particularly important for low-mass particles, the Law of Dulong and Petit already fails at room temperature for some light elements, such as beryllium and carbon. It also fails for some heavier elements for various reasons beyond what we can cover.)
The strategy for solving these problems is the same as the one in Phase Changes for the effects of heat transfer. The only new feature is that you should determine whether the case just presented—ideal gases at constant volume—applies to the problem. (For solid elements, looking up the specific heat capacity is generally better than estimating it from the Law of Dulong and Petit.) In the case of an ideal gas, determine the number d of degrees of freedom from the number of atoms in the gas molecule and use it to calculate \(C_V\) (or use \(C_V\) to solve for d).
A 300-g piece of solid gallium (a metal used in semiconductor devices) at its melting point of only \(30.0^oC\) is in contact with 12.0 moles of air (assumed diatomic) at \(95.0^oC\) in an insulated container. When the air reaches equilibrium with the gallium, 202 g of the gallium have melted. Based on those data, what is the heat of fusion of gallium? Assume the volume of the air does not change and there are no other heat transfers.
Strategy
We’ll use the equation \(Q_{hot} + Q_{cold} = 0\). As some of the gallium doesn’t melt, we know the final temperature is still the melting point. Then the only \(Q_{hot}\) is the heat lost as the air cools, \(Q_{hot} = n_{air}C_V\Delta T\), where \(C_V = 5R/2\). The only \(Q_{cold}\) is the latent heat of fusion of the gallium, \(Q_{cold} = m_{Ga}L_f\). It is positive because heat flows into the gallium.
Solution
- Set up the equation:\[n_{air}C_V\Delta T + m_{Ga}L_f = 0.\nonumber \]
- Substitute the known values and solve: \[(12.0 \, mol) \left(\dfrac{5}{2}\right) \left(8.31 \dfrac{J}{mol \cdot \, ^oC}\right)(30.0^oC - 95.0^oC) + (0.202 \, kg)L_f = 0.\nonumber \]
We solve to find that the heat of fusion of gallium is 80.2 kJ/kg.


