11.5: Precession of a Gyroscope
- Page ID
- 4037
- Describe the physical processes underlying the phenomenon of precession
- Calculate the precessional angular velocity of a gyroscope
Figure \(\PageIndex{1}\) shows a gyroscope, defined as a spinning disk in which the axis of rotation is free to assume any orientation. When spinning, the orientation of the spin axis is unaffected by the orientation of the body that encloses it. The body or vehicle enclosing the gyroscope can be moved from place to place and the orientation of the spin axis will remain the same. This makes gyroscopes very useful in navigation, especially where magnetic compasses can’t be used, such as in manned and unmanned spacecraft, intercontinental ballistic missiles, unmanned aerial vehicles, and satellites like the Hubble Space Telescope.
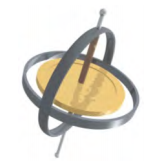
We illustrate the precession of a gyroscope with an example of a top in the next two figures. If the top is placed on a flat surface near the surface of Earth at an angle to the vertical and is not spinning, it will fall over, due to the force of gravity producing a torque acting on its center of mass. This is shown in Figure \(\PageIndex{2a}\). However, if the top is spinning on its axis, rather than topple over due to this torque, it precesses about the vertical, shown in \(\PageIndex{2b}\). This is due to the torque on the center of mass, which provides the change in angular momentum.
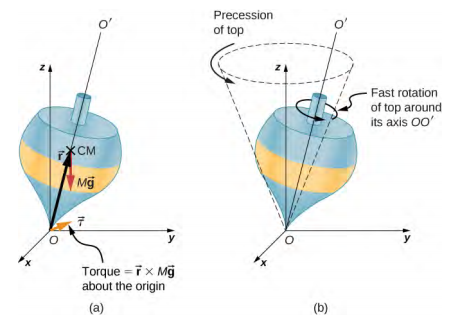
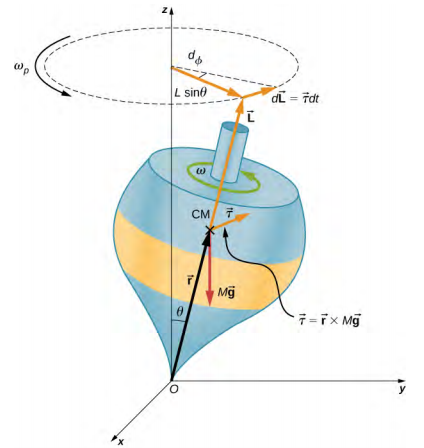
Figure \(\PageIndex{3}\) shows the forces acting on a spinning top. The torque produced is perpendicular to the angular momentum vector. This changes the direction of the angular momentum vector \(\vec{L}\) according to d\(\vec{L}\) = \(\vec{\tau}\)dt, but not its magnitude. The top precesses around a vertical axis, since the torque is always horizontal and perpendicular to \(\vec{L}\). If the top is not spinning, it acquires angular momentum in the direction of the torque, and it rotates around a horizontal axis, falling over just as we would expect.
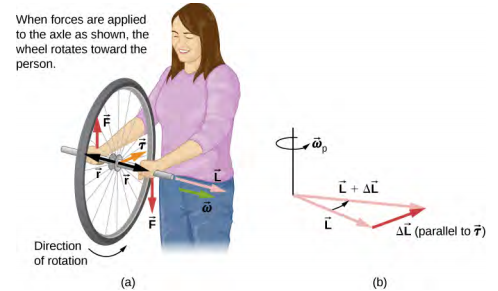
We can experience this phenomenon first hand by holding a spinning bicycle wheel and trying to rotate it about an axis perpendicular to the spin axis. As shown in Figure \(\PageIndex{4}\), the person applies forces perpendicular to the spin axis in an attempt to rotate the wheel, but instead, the wheel axis starts to change direction to her left due to the applied torque.
We all know how easy it is for a bicycle to tip over when sitting on it at rest. But when riding the bicycle at a good pace, it is harder to tip it over because we must change the angular momentum vector of the spinning wheels.
View this video on gyroscope precession for a complete demonstration of precession of the bicycle wheel.
Also, when a spinning disk is put in a box such as a Blu-Ray player, try to move it. It is easy to translate the box in a given direction but difficult to rotate it about an axis perpendicular to the axis of the spinning disk, since we are putting a torque on the box that will cause the angular momentum vector of the spinning disk to precess.
We can calculate the precession rate of the top in Figure \(\PageIndex{3}\). From Figure \(\PageIndex{3}\), we see that the magnitude of the torque is
\[\tau = rMg \sin \theta \ldotp\]
Thus,
\[dL = rMg \sin \theta dt \ldotp\]
The angle the top precesses through in time dt is
\[d \phi = \frac{dL}{L \sin \theta} = \frac{rMg \sin \theta}{L \sin \theta} dt = \frac{rMg}{L} dt \ldotp\]
The precession angular velocity is \(\omega_{P} = \frac{d \phi}{dt}\) and from this equation we see that
\[\omega_{P} = \frac{rMg}{L} \ldotp\]
or, since L = I\(\omega\),
\[\omega_{P} = \frac{rMg}{I \omega} \ldotp \label{11.12}\]
In this derivation, we assumed that \(\omega_{P}\) << \(\omega\), that is, that the precession angular velocity is much less than the angular velocity of the gyroscope disk. The precession angular velocity adds a small component to the angular momentum along the z-axis. This is seen in a slight bob up and down as the gyroscope precesses, referred to as nutation.
Earth itself acts like a gigantic gyroscope. Its angular momentum is along its axis and currently points at Polaris, the North Star. But Earth is slowly precessing (once in about 26,000 years) due to the torque of the Sun and the Moon on its nonspherical shape.
A gyroscope spins with its tip on the ground and is spinning with negligible frictional resistance. The disk of the gyroscope has mass 0.3 kg and is spinning at 20 rev/s. Its center of mass is 5.0 cm from the pivot and the radius of the disk is 5.0 cm. What is the precessional period of the gyroscope?
Strategy
We use Equation \ref{11.12} to find the precessional angular velocity of the gyroscope. This allows us to find the period of precession.
Solution
The moment of inertia of the disk is
\[I = \frac{1}{2} mr^{2} = \frac{1}{2} (0.30\; kg)(0.05\; m)^{2} = 3.75 \times 10^{-4}\; kg\; \cdotp m^{2} \ldotp \nonumber\]
The angular velocity of the disk is
\[20.0\; rev/s = (20.0)(2 \pi)\; rad/s = 125.66\; rad/s \ldotp \nonumber\]
We can now substitute in Equation \ref{11.12}. The precessional angular velocity is
\[\omega_{P} = \frac{rMg}{I \omega} = \frac{(0.05\; m)(0.3\; kg)(9.8\; m/s^{2})}{(3.75 \times 10^{-4}\; kg\; \cdotp m^{2})(125.66\; rad/s)} = 3.12\; rad/s \ldotp \nonumber\]
The precessional period of the gyroscope is
\[T_{P} = \frac{2 \pi}{3.12\; rad/s} = 2.0\; s \ldotp \nonumber\]
Significance
The precessional angular frequency of the gyroscope, 3.12 rad/s, or about 0.5 rev/s, is much less than the angular velocity 20 rev/s of the gyroscope disk. Therefore, we don’t expect a large component of the angular momentum to arise due to precession, and Equation 11.12 is a good approximation of the precessional angular velocity.
A top has a precession frequency of 5.0 rad/s on Earth. What is its precession frequency on the Moon?


