17.4: Sound Intensity
- Page ID
- 4078
- Define the term intensity
- Explain the concept of sound intensity level
- Describe how the human ear translates sound
In a quiet forest, you can sometimes hear a single leaf fall to the ground. But when a passing motorist has his stereo turned up, you cannot even hear what the person next to you in your car is saying (Figure \(\PageIndex{1}\)). We are all very familiar with the loudness of sounds and are aware that loudness is related to how energetically the source is vibrating. High noise exposure is hazardous to hearing, which is why it is important for people working in industrial settings to wear ear protection. The relevant physical quantity is sound intensity, a concept that is valid for all sounds whether or not they are in the audible range.

Previously, we defined intensity as the power per unit area carried by a wave. Power is the rate at which energy is transferred by the wave. In equation form, intensity \(I\) is
\[I = \frac{P}{A}, \label{17.8}\]
where \(P\) is the power through an area \(A\). The SI unit for \(I\) is W/m2. If we assume that the sound wave is spherical, and that no energy is lost to thermal processes, the energy of the sound wave is spread over a larger area as distance increases, so the intensity decreases. The area of a sphere is \(A = 4 \pi r^2\). As the wave spreads out from \(r_1\) to \(r_2\), the energy also spreads out over a larger area:
\[\begin{align} P_{1} & = P_{2} \\[4pt] I_{1} 4 \pi r_{1}^{2} & = I_{2} 4 \pi r_{2}^{2} \\[4pt] I_{2} &= I_{1} \left(\dfrac{r_{1}}{r_{2}}\right)^{2} \ldotp \label{17.9} \end{align}\]
The intensity decreases as the wave moves out from the source. In an inverse square relationship, such as the intensity, when you double the distance, the intensity decreases to one quarter,
\[I_{2} = I_{1} \left(\dfrac{r_{1}}{r_{2}}\right)^{2} = I_{1} \left(\dfrac{r_{1}}{2r_{1}}\right)^{2} = \frac{1}{4} I_{1} \ldotp\]
Generally, when considering the intensity of a sound wave, we take the intensity to be the time-averaged value of the power, denoted by \(⟨P⟩\), divided by the area,
\[I = \frac{\langle P \rangle}{A} \ldotp \label{17.10}\]
The intensity of a sound wave is proportional to the change in the pressure squared and inversely proportional to the density and the speed. Consider a parcel of a medium initially undisturbed and then influenced by a sound wave at time t, as shown in Figure \(\PageIndex{2}\).
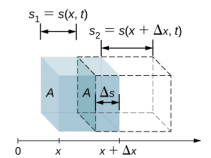
As the sound wave moves through the parcel, the parcel is displaced and may expand or contract. If \(s_2 > s_1\), the volume has increased and the pressure decreases. If \(s_2 < s_1,\) the volume has decreased and the pressure increases. The change in the volume is
\[\begin{align} \Delta V &= A \Delta s \\[4pt] &= A(s_{2} - s_{1}) \\[4pt] &= A[s(x + \Delta x,t)-s(x,t)] \ldotp \end{align}\]
The fractional change in the volume is the change in volume divided by the original volume:
\[ \begin{align} \frac{dV}{V} &= \lim_{\Delta x \rightarrow 0} \frac{A[s(x + \Delta x,t)-s(x,t)]}{A \Delta x} \\[4pt] &= \frac{\partial s(x,t)}{\partial x} \ldotp \end{align}\]
The fractional change in volume is related to the pressure fluctuation by the bulk modulus
\[\beta = − \frac{\Delta p(x, t)}{\frac{dV}{V}}.\]
Recall that the minus sign is required because the volume is inversely related to the pressure. (We use lowercase \(p\) for pressure to distinguish it from power, denoted by \(P\).) The change in pressure is therefore
\[\Delta p(x, t) = − \beta \frac{dV}{V} = − \beta \frac{\partial s(x, t)}{\partial x}.\]
If the sound wave is sinusoidal, then the displacement as shown in Equation 17.2 is
\[s(x, t) = s_{max} \cos(kx ∓ \omega t + \phi)\]
and the pressure is found to be
\[ \begin{align} \Delta p(x,t) &= - \beta \frac{dV}{V} \\[4pt] &= - \beta \frac{\partial s(x,t)}{\partial x} \\[4pt] &= \beta ks_{max} \sin (kx - \omega t + \phi) \\[4pt] &= \Delta p_{max} \sin (kx - \omega t + \phi) \ldotp \end{align}\]
The intensity of the sound wave is the power per unit area, and the power is the force times the velocity,
\[I = \frac{P}{A} = \frac{Fv}{A} = pv.\]
Here, the velocity is the velocity of the oscillations of the medium, and not the velocity of the sound wave. The velocity of the medium is the time rate of change in the displacement:
\[v(x,t) = \frac{\partial}{\partial y} s(x,t) = \frac{\partial}{\partial y} [s_{max} \cos (kx - \omega t + \phi)] = s_{max} \omega \sin (kx - \omega t + \phi) \ldotp\]
Thus, the intensity becomes
\[\begin{align} I & = \Delta p(x,t)\; v(x,t) \\[4pt] & = \beta ks_{max} \sin (kx - \omega t + \phi)[s_{max} \omega \sin (kx - \omega t + \phi)] \\[4pt] & = \beta k \omega s_{max}^{2} \sin^{2} (kx - \omega t + \phi) \ldotp \end{align}\]
To find the time-averaged intensity over one period \(T = \frac{2 \pi}{\omega}\) for a position \(x\), we integrate over the period,
\[I = \frac{\beta k \omega s_{max}^{2}}{2}.\]
Using \(\Delta p_{max} = \beta ks_{max}\), \(v = \sqrt{\frac{\beta}{\rho}}\), and \(v = \frac{\omega}{k}\), we obtain
\[ \begin{align*} I &= \frac{\beta k \omega s_{max}^{2}}{2} \\[4pt] &= \frac{\beta^{2} k^{2} \omega s_{max}^{2}}{2 \beta k} \\[4pt] &= \frac{\omega (\Delta p_{max})^{2}}{2 (\rho v^{2}) k} \\[4pt] &= \frac{v (\Delta p_{max})^{2}}{2 (\rho v^{2})} \\[4pt] &= \frac{(\Delta p_{max})^{2}}{2 \rho v} \ldotp \end{align*}\]
That is, the intensity of a sound wave is related to its amplitude squared by
\[I = \frac{(\Delta p_{max})^{2}}{2 \rho v} \ldotp \label{17.11}\]
Here, \(\Delta\)pmax is the pressure variation or pressure amplitude in units of pascals (Pa) or N/m2. The energy (as kinetic energy \(\frac{1}{2} mv^2\)) of an oscillating element of air due to a traveling sound wave is proportional to its amplitude squared. In this equation, \(\rho\) is the density of the material in which the sound wave travels, in units of kg/m3, and \(v\) is the speed of sound in the medium, in units of m/s. The pressure variation is proportional to the amplitude of the oscillation, so \(I\) varies as (\(\Delta p)^2\). This relationship is consistent with the fact that the sound wave is produced by some vibration; the greater its pressure amplitude, the more the air is compressed in the sound it creates.
Human Hearing and Sound Intensity Levels
As stated earlier in this chapter, hearing is the perception of sound. The hearing mechanism involves some interesting physics. The sound wave that impinges upon our ear is a pressure wave. The ear is a transducer that converts sound waves into electrical nerve impulses in a manner much more sophisticated than, but analogous to, a microphone. Figure \(\PageIndex{3}\) shows the anatomy of the ear.
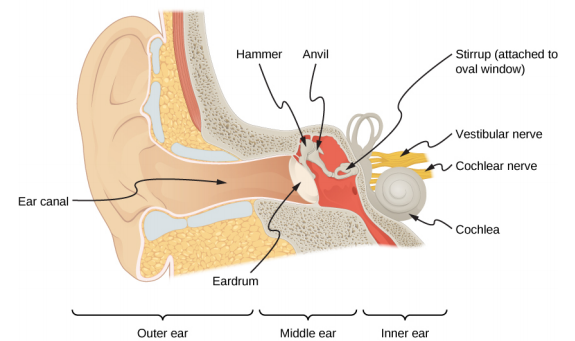
The outer ear, or ear canal, carries sound to the recessed, protected eardrum. The air column in the ear canal resonates and is partially responsible for the sensitivity of the ear to sounds in the 2000–5000-Hz range. The middle ear converts sound into mechanical vibrations and applies these vibrations to the cochlea.
Watch this video for a more detailed discussion of the workings of the human ear.
The range of intensities that the human ear can hear depends on the frequency of the sound, but, in general, the range is quite large. The minimum threshold intensity that can be heard is I0 = 10−12 W/m2. Pain is experienced at intensities of Ipain = 1 W/m2. Measurements of sound intensity (in units of W/m2) are very cumbersome due to this large range in values. For this reason, as well as for other reasons, the concept of sound intensity level was proposed.
The sound intensity level \(\beta\) of a sound, measured in decibels, having an intensity I in watts per meter squared, is defined as
\[\beta (dB) = \log_{10} \left(\dfrac{I}{I_{0}}\right), \label{17.12}\]
where I0 = 10−12 W/m2 is a reference intensity, corresponding to the threshold intensity of sound that a person with normal hearing can perceive at a frequency of 1.00 kHz. It is more common to consider sound intensity levels in dB than in W/m2. How human ears perceive sound can be more accurately described by the logarithm of the intensity rather than directly by the intensity. Because β is defined in terms of a ratio, it is a unitless quantity, telling you the level of the sound relative to a fixed standard (10−12 W/m2). The units of decibels (dB) are used to indicate this ratio is multiplied by 10 in its definition. The bel, upon which the decibel is based, is named for Alexander Graham Bell, the inventor of the telephone. The decibel level of a sound having the threshold intensity of 10−12 W/m2 is \(\beta\) = 0 dB, because log10 1 = 0. Table \(\PageIndex{2}\) gives levels in decibels and intensities in watts per meter squared for some familiar sounds. The ear is sensitive to as little as a trillionth of a watt per meter squared—even more impressive when you realize that the area of the eardrum is only about 1 cm2, so that only 10−16 W falls on it at the threshold of hearing. Air molecules in a sound wave of this intensity vibrate over a distance of less than one molecular diameter, and the gauge pressures involved are less than 10−9 atm.
| Sound intensity level \(\beta\) (dB) | Intensity | Example/effect |
|---|---|---|
| 0 | 1 x 10−12 | Threshold of hearing at 1000 Hz |
| 10 | 1 x 10−11 | Rustle of leaves |
| 20 | 1 x 10−10 | Whisper at 1-m distance |
| 30 | 1 x 10−9 | Quiet home |
| 40 | 1 x 10−8 | Average home |
| 50 | 1 x 10−7 | Average office, soft music |
| 60 | 1 x 10−6 | Normal conversation |
| 70 | 1 x 10−5 | Noisy office, busy traffic |
| 80 | 1 x 10−4 | Loud radio, classroom lecture |
| 90 | 1 x 10−3 | Inside a heavy truck; damage from prolonged exposure[1] |
| 100 | 1 x 10−2 | Noisy factory, siren at 30 m; damage from 8 h per day exposure |
| 110 | 1 x 10−1 | Damage from 30 min per day exposure |
| 120 | 1 | Loud rock concert; pneumatic chipper at 2 m; threshold of pain |
| 140 | 1 x 102 | Jet airplane at 30 m; severe pain, damage in seconds |
| 160 | 1 x 104 | Bursting of eardrums |
[1] Several government agencies and health-related professional associations recommend that 85 dB not be exceeded for 8-hour daily exposures in the absence of hearing protection.
An observation readily verified by examining Table \(\PageIndex{2}\) or by using Equation \ref{17.12} is that each factor of 10 in intensity corresponds to 10 dB. For example, a 90-dB sound compared with a 60-dB sound is 30 dB greater, or three factors of 10 (that is, 103 times) as intense. Another example is that if one sound is 107 as intense as another, it is 70 dB higher (Table \(\PageIndex{2}\)).
| \(\frac{I_{2}}{I_{1}}\) | \(\beta_{2} - \beta_{1}\) |
|---|---|
| 2.0 | 3.0 dB |
| 5.0 | 7.0 dB |
| 10.0 | 10.0 dB |
| 100.0 | 20.0 dB |
| 1000.0 | 30.0 dB |
Calculate the sound intensity level in decibels for a sound wave traveling in air at 0°C and having a pressure amplitude of 0.656 Pa.
Strategy
We are given \(Δp\), so we can calculate \(I\) using the equation
\[I = \dfrac{(\Delta p)^2}{2 \rho vw}.\]
Using \(I\), we can calculate \(\beta\) straight from its definition in
\[\beta (dB) = 10 \log_{10} \left(\dfrac{I}{I_{0}}\right).\]
Solution
- Identify knowns: Sound travels at 331 m/s in air at 0 °C. Air has a density of 1.29 kg/m3 at atmospheric pressure and 0 °C.
- Enter these values and the pressure amplitude into I = \(\frac{(\Delta p)^{2}}{2 \rho v}\). $$I = \frac{(\Delta p)^{2}}{2 \rho v} = \frac{(0.656\; Pa)^{2}}{2(1.29\; kg/m^{3})(331\; m/s)} = 5.04 \times 10^{-4}\; W/m^{2} \ldotp$$
- Enter the value for I and the known value for I0 into \(\beta\)(dB) = 10 log10\(\left(\dfrac{I}{I_{0}}\right)\). Calculate to find the sound intensity level in decibels: $$10 \log_{10} (5.04 \times 10^{8}) = (10\; dB)(8.70) = 87\; dB \ldotp$$
Significance
This 87-dB sound has an intensity five times as great as an 80-dB sound. So a factor of five in intensity corresponds to a difference of 7 dB in sound intensity level. This value is true for any intensities differing by a factor of five.
Show that if one sound is twice as intense as another, it has a sound level about 3 dB higher.
Strategy
We are given that the ratio of two intensities is 2 to 1, and are then asked to find the difference in their sound levels in decibels. We can solve this problem by using of the properties of logarithms.
Solution
- Identify knowns: The ratio of the two intensities is 2 to 1, or $$\frac{I_{2}}{I_{1}} = 2.00 \ldotp$$We wish to show that the difference in sound levels is about 3 dB. That is, we want to show: $$\beta_{2} - \beta_{1} = 3\; dB \ldotp$$Note that $$log_{10} b - \log_{10} a = \log_{10} \left(\dfrac{b}{a}\right) \ldotp$$
- Use the definition of \(\beta\) to obtain $$\beta_{2} - \beta_{1} = 10 \log_{10} \left(\dfrac{I_{2}}{I_{1}}\right) = 10 \log_{10} 2.00 = (10\; dB)(0.301) \ldotp$$Thus, $$\beta_{2} - \beta_{1} = 3.01\; dB \ldotp$$
Significance
This means that the two sound intensity levels differ by 3.01 dB, or about 3 dB, as advertised. Note that because only the ratio \(\frac{I_{2}}{I_{1}}\) is given (and not the actual intensities), this result is true for any intensities that differ by a factor of two. For example, a 56.0-dB sound is twice as intense as a 53.0-dB sound, a 97.0-dB sound is half as intense as a 100-dB sound, and so on.
Identify common sounds at the levels of 10 dB, 50 dB, and 100 dB.
Another decibel scale is also in use, called the sound pressure level, based on the ratio of the pressure amplitude to a reference pressure. This scale is used particularly in applications where sound travels in water. It is beyond the scope of this text to treat this scale because it is not commonly used for sounds in air, but it is important to note that very different decibel levels may be encountered when sound pressure levels are quoted.
Hearing and Pitch
The human ear has a tremendous range and sensitivity. It can give us a wealth of simple information—such as pitch, loudness, and direction.
The perception of frequency is called pitch. Typically, humans have excellent relative pitch and can discriminate between two sounds if their frequencies differ by 0.3% or more. For example, 500.0 and 501.5 Hz are noticeably different. Musical notes are sounds of a particular frequency that can be produced by most instruments and in Western music have particular names, such as A-sharp, C, or E-flat.
The perception of intensity is called loudness. At a given frequency, it is possible to discern differences of about 1 dB, and a change of 3 dB is easily noticed. But loudness is not related to intensity alone. Frequency has a major effect on how loud a sound seems. Sounds near the high- and low-frequency extremes of the hearing range seem even less loud, because the ear is less sensitive at those frequencies. When a violin plays middle C, there is no mistaking it for a piano playing the same note. The reason is that each instrument produces a distinctive set of frequencies and intensities. We call our perception of these combinations of frequencies and intensities tone quality or, more commonly, the timbre of the sound. Timbre is the shape of the wave that arises from the many reflections, resonances, and superposition in an instrument.
A unit called a phon is used to express loudness numerically. Phons differ from decibels because the phon is a unit of loudness perception, whereas the decibel is a unit of physical intensity. Figure \(\PageIndex{4}\) shows the relationship of loudness to intensity (or intensity level) and frequency for persons with normal hearing. The curved lines are equal-loudness curves. Each curve is labeled with its loudness in phons. Any sound along a given curve is perceived as equally loud by the average person. The curves were determined by having large numbers of people compare the loudness of sounds at different frequencies and sound intensity levels. At a frequency of 1000 Hz, phons are taken to be numerically equal to decibels.
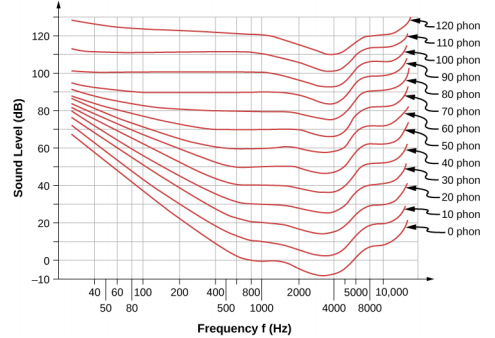
- What is the loudness in phons of a 100-Hz sound that has an intensity level of 80 dB?
- What is the intensity level in decibels of a 4000-Hz sound having a loudness of 70 phons?
- At what intensity level will an 8000-Hz sound have the same loudness as a 200-Hz sound at 60 dB?
Strategy
The graph in Figure \(\PageIndex{4}\) should be referenced to solve this example. To find the loudness of a given sound, you must know its frequency and intensity level, locate that point on the square grid, and then interpolate between loudness curves to get the loudness in phons. Once that point is located, the intensity level can be determined from the vertical axis.
Solution
- Identify knowns: The square grid of the graph relating phons and decibels is a plot of intensity level versus frequency—both physical quantities: 100 Hz at 80 dB lies halfway between the curves marked 70 and 80 phons. Find the loudness: 75 phons.
- Identify knowns: Values are given to be 4000 Hz at 70 phons. Follow the 70-phon curve until it reaches 4000 Hz. At that point, it is below the 70 dB line at about 67 dB. Find the intensity level: 67 dB.
- Locate the point for a 200 Hz and 60 dB sound. Find the loudness: This point lies just slightly above the 50-phon curve, and so its loudness is 51 phons. Look for the 51-phon level is at 8000 Hz: 63 dB.
Significance
These answers, like all information extracted from Figure \(\PageIndex{4}\), have uncertainties of several phons or several decibels, partly due to difficulties in interpolation, but mostly related to uncertainties in the equal-loudness curves.
Describe how amplitude is related to the loudness of a sound.
In this section, we discussed the characteristics of sound and how we hear, but how are the sounds we hear produced? Interesting sources of sound are musical instruments and the human voice, and we will discuss these sources. But before we can understand how musical instruments produce sound, we need to look at the basic mechanisms behind these instruments. The theories behind the mechanisms used by musical instruments involve interference, superposition, and standing waves, which we discuss in the next section.


