6.5: Bohr’s Model of the Hydrogen Atom
- Page ID
- 4523
By the end of this section, you will be able to:
- Explain the difference between the absorption spectrum and the emission spectrum of radiation emitted by atoms
- Describe the Rutherford gold foil experiment and the discovery of the atomic nucleus
- Explain the atomic structure of hydrogen
- Describe the postulates of the early quantum theory for the hydrogen atom
- Summarize how Bohr’s quantum model of the hydrogen atom explains the radiation spectrum of atomic hydrogen
Historically, Bohr’s model of the hydrogen atom is the very first model of atomic structure that correctly explained the radiation spectra of atomic hydrogen. The model has a special place in the history of physics because it introduced an early quantum theory, which brought about new developments in scientific thought and later culminated in the development of quantum mechanics. To understand the specifics of Bohr’s model, we must first review the nineteenth-century discoveries that prompted its formulation.
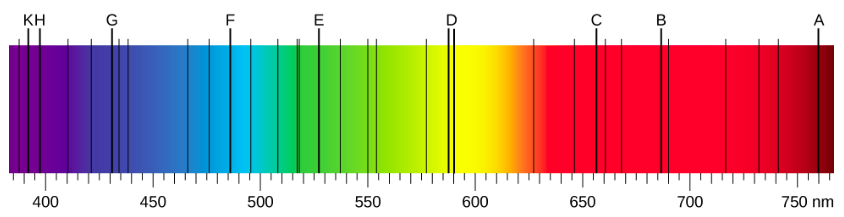
When we use a prism to analyze white light coming from the sun, several dark lines in the solar spectrum are observed (Figure \(\PageIndex{1}\)). Solar absorption lines are called Fraunhofer lines after Joseph von Fraunhofer, who accurately measured their wavelengths. During 1854–1861, Gustav Kirchhoff and Robert Bunsen discovered that for the various chemical elements, the line emission spectrum of an element exactly matches its line absorption spectrum. The difference between the absorption spectrum and the emission spectrum is explained in Figure \(\PageIndex{2}\).
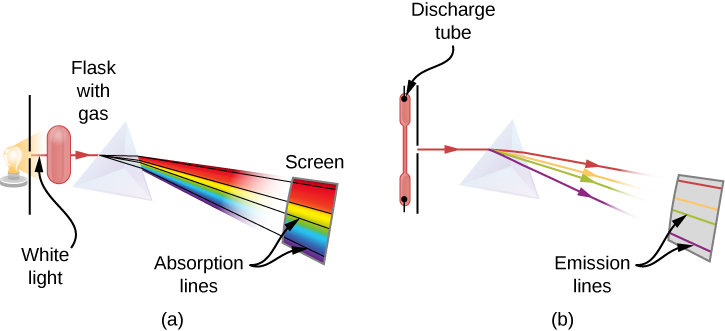
An absorption spectrum is observed when light passes through a gas. This spectrum appears as black lines that occur only at certain wavelengths on the background of the continuous spectrum of white light (Figure \(\PageIndex{2}\)). The missing wavelengths tell us which wavelengths of the radiation are absorbed by the gas. The emission spectrum is observed when light is emitted by a gas. This spectrum is seen as colorful lines on the black background (Figures \(\PageIndex{3}\) and \(\PageIndex{4}\)). Positions of the emission lines tell us which wavelengths of the radiation are emitted by the gas. Each chemical element has its own characteristic emission spectrum. For each element, the positions of its emission lines are exactly the same as the positions of its absorption lines. This means that atoms of a specific element absorb radiation only at specific wavelengths and radiation that does not have these wavelengths is not absorbed by the element at all. This also means that the radiation emitted by atoms of each element has exactly the same wavelengths as the radiation they absorb.


Emission spectra of the elements have complex structures; they become even more complex for elements with higher atomic numbers. The simplest spectrum, shown in Figure \(\PageIndex{4}\), belongs to the hydrogen atom. Only four lines are visible to the human eye. As you read from right to left in Figure \(\PageIndex{4}\), these lines are: red (656 nm), called the \(H-\alpha\) line; aqua (486 nm), blue (434 nm), and violet (410 nm). The lines with wavelengths shorter than 400 nm appear in the ultraviolet part of the spectrum (Figure \(\PageIndex{4}\), far left) and are invisible to the human eye. There are infinitely many invisible spectral lines in the series for hydrogen.
An empirical formula to describe the positions (wavelengths) λ of the hydrogen emission lines in this series was discovered in 1885 by Johann Balmer. It is known as the Balmer formula:
\[ \dfrac{1}{\lambda} = R_H \left( \dfrac{1}{2^2} - \dfrac{1}{n^2}\right). \label{balmer} \]
The constant \(R_H = 1.09737 \times 10^7 m^{-1}\) is called the Rydberg constant for hydrogen. In Equation \ref{balmer}, the positive integer n takes on values \(n = 3, 4,5,6\) for the four visible lines in this series. The series of emission lines given by the Balmer formula is called the Balmer series for hydrogen. Other emission lines of hydrogen that were discovered in the twentieth century are described by the Rydberg formula, which summarizes all of the experimental data:
\[ \dfrac{1}{\lambda} = R_H \left( \dfrac{1}{n_f^2} - \dfrac{1}{n_i^2}\right)\label{rydberg} \]
where \(n_i = n_f > n_i\) (in integer steps).
When \(n_f = 1\), the series of spectral lines is called the Lyman series. When \(n_f = 2\), the series is called the Balmer series, and in this case, the Rydberg formula coincides with the Balmer formula (Equation \ref{balmer}). When \(n_f = 3\), the series is called the Paschen series. When \(n_f = 4\), the series is called the Brackett series. When \(n_f = 5\), the series is called the Pfund series. When \(n_f = 6\), we have the Humphreys series. As you may guess, there are infinitely many such spectral bands in the spectrum of hydrogen because \(n_f\) can be any positive integer number.
The Rydberg formula for hydrogen gives the exact positions of the spectral lines as they are observed in a laboratory; however, at the beginning of the twentieth century, nobody could explain why it worked so well. The Rydberg formula remained unexplained until the first successful model of the hydrogen atom was proposed in 1913.
Calculate the longest and the shortest wavelengths in the Balmer series.
Strategy
We can use either the Balmer formula (Equation \ref{balmer}) or the Rydberg formula (Equation \ref{rydberg}). The longest wavelength is obtained when \(1/n_i\)i is largest, which is when \(n_i = n_f + 1 = 3\), because \(n_f = 2\) for the Balmer series. The smallest wavelength is obtained when \(1/n_i\) is smallest, which is \(1/n_i \rightarrow 0\) when \(n_i \rightarrow \infty\).
Solution
The long-wave limit:
\[ \dfrac{1}{\lambda} = R_H \left( \dfrac{1}{2^2} - \dfrac{1}{3^2}\right) = (1.09737 \times 10^7) \dfrac{1}{m} \left( \dfrac{1}{4} - \dfrac{1}{9}\right) \Rightarrow \lambda = 656.3 \, nm \nonumber \]
The short-wave limit:
\[ \dfrac{1}{\lambda} = R_H \left( \dfrac{1}{2^2} - 0\right) = (1.09737 \times 10^7) \dfrac{1}{m} \left( \dfrac{1}{4} \right) \Rightarrow \lambda = 364.6 \, nm. \nonumber \]
Significance
Note that there are infinitely many spectral lines lying between these two limits.
What are the limits of the Lyman series? Can you see these spectral lines?
- Answer
-
121.5 nm and 91.1 nm; no, these spectral bands are in the ultraviolet
The key to unlocking the mystery of atomic spectra is in understanding atomic structure. Scientists have long known that matter is made of atoms. According to nineteenth-century science, atoms are the smallest indivisible quantities of matter. This scientific belief was shattered by a series of groundbreaking experiments that proved the existence of subatomic particles, such as electrons, protons, and neutrons.
The electron was discovered and identified as the smallest quantity of electric charge by J.J. Thomson in 1897 in his cathode ray experiments, also known as β-ray experiments: A β-ray is a beam of electrons. In 1904, Thomson proposed the first model of atomic structure, known as the “plum pudding” model, in which an atom consisted of an unknown positively charged matter with negative electrons embedded in it like plums in a pudding. Around 1900, E. Rutherford, and independently, Paul Ulrich Villard, classified all radiation known at that time as \(\alpha\)-rays, \(β\)-rays, and \(\gamma\)-rays (a \(\gamma\)-ray is a beam of highly energetic photons). In 1907, Rutherford and Thomas Royds used spectroscopy methods to show that positively charged particles of \(\alpha\)-radiation (called \(\alpha\)-particles) are in fact doubly ionized atoms of helium. In 1909, Rutherford, Ernest Marsden, and Hans Geiger used \(\alpha\)-particles in their famous scattering experiment that disproved Thomson’s model (see Linear Momentum and Collisions).
In the Rutherford gold foil experiment (also known as the Geiger–Marsden experiment), α-particles were incident on a thin gold foil and were scattered by gold atoms inside the foil (see Types of Collisions). The outgoing particles were detected by a 360° scintillation screen surrounding the gold target (for a detailed description of the experimental setup, see Linear Momentum and Collisions). When a scattered particle struck the screen, a tiny flash of light (scintillation) was observed at that location. By counting the scintillations seen at various angles with respect to the direction of the incident beam, the scientists could determine what fraction of the incident particles were scattered and what fraction were not deflected at all. If the plum pudding model were correct, there would be no back-scattered α-particles. However, the results of the Rutherford experiment showed that, although a sizable fraction of α-particles emerged from the foil not scattered at all as though the foil were not in their way, a significant fraction of α-particles were back-scattered toward the source. This kind of result was possible only when most of the mass and the entire positive charge of the gold atom were concentrated in a tiny space inside the atom.
In 1911, Rutherford proposed a nuclear model of the atom. In Rutherford’s model, an atom contained a positively charged nucleus of negligible size, almost like a point, but included almost the entire mass of the atom. The atom also contained negative electrons that were located within the atom but relatively far away from the nucleus. Ten years later, Rutherford coined the name proton for the nucleus of hydrogen and the name neutron for a hypothetical electrically neutral particle that would mediate the binding of positive protons in the nucleus (the neutron was discovered in 1932 by James Chadwick). Rutherford is credited with the discovery of the atomic nucleus; however, the Rutherford model of atomic structure does not explain the Rydberg formula for the hydrogen emission lines.
Bohr’s model of the hydrogen atom, proposed by Niels Bohr in 1913, was the first quantum model that correctly explained the hydrogen emission spectrum. Bohr’s model combines the classical mechanics of planetary motion with the quantum concept of photons. Once Rutherford had established the existence of the atomic nucleus, Bohr’s intuition that the negative electron in the hydrogen atom must revolve around the positive nucleus became a logical consequence of the inverse-square-distance law of electrostatic attraction. Recall that Coulomb’s law describing the attraction between two opposite charges has a similar form to Newton’s universal law of gravitation in the sense that the gravitational force and the electrostatic force are both decreasing as \(1/r^2\), where r is the separation distance between the bodies. In the same way as Earth revolves around the sun, the negative electron in the hydrogen atom can revolve around the positive nucleus. However, an accelerating charge radiates its energy. Classically, if the electron moved around the nucleus in a planetary fashion, it would be undergoing centripetal acceleration, and thus would be radiating energy that would cause it to spiral down into the nucleus. Such a planetary hydrogen atom would not be stable, which is contrary to what we know about ordinary hydrogen atoms that do not disintegrate. Moreover, the classical motion of the electron is not able to explain the discrete emission spectrum of hydrogen.
To circumvent these two difficulties, Bohr proposed the following three postulates of Bohr’s model:
- The negative electron moves around the positive nucleus (proton) in a circular orbit. All electron orbits are centered at the nucleus. Not all classically possible orbits are available to an electron bound to the nucleus.
- The allowed electron orbits satisfy the first quantization condition: In the nth orbit, the angular momentum \(L_n\) of the electron can take only discrete values: \[L_n = n\hbar, \, where \, n = 1,2,3, . . . \nonumber \] This postulate says that the electron’s angular momentum is quantized. Denoted by \(r_n\) and \(v_n\), respectively, the radius of the nth orbit and the electron’s speed in it, the first quantization condition can be expressed explicitly as \[m_ev_nr_n = n\hbar. \label{6.34} \]
- An electron is allowed to make transitions from one orbit where its energy is \(E_n\) to another orbit where its energy is \(E_m\). When an atom absorbs a photon, the electron makes a transition to a higher-energy orbit. When an atom emits a photon, the electron transits to a lower-energy orbit. Electron transitions with the simultaneous photon absorption or photon emission take place instantaneously. The allowed electron transitions satisfy the second quantization condition: \[hf = |E_n - E_m| \nonumber \] where \(hf\) is the energy of either an emitted or an absorbed photon with frequency \(f\). The second quantization condition states that an electron’s change in energy in the hydrogen atom is quantized.
These three postulates of the early quantum theory of the hydrogen atom allow us to derive not only the Rydberg formula, but also the value of the Rydberg constant and other important properties of the hydrogen atom such as its energy levels, its ionization energy, and the sizes of electron orbits. Note that in Bohr’s model, along with two nonclassical quantization postulates, we also have the classical description of the electron as a particle that is subjected to the Coulomb force, and its motion must obey Newton’s laws of motion. The hydrogen atom, as an isolated system, must obey the laws of conservation of energy and momentum in the way we know from classical physics. Having this theoretical framework in mind, we are ready to proceed with our analysis.
Electron Orbits
To obtain the size \(r_n\) of the electron’s nth orbit and the electron’s speed \(v_n\) in it, we turn to Newtonian mechanics. As a charged particle, the electron experiences an electrostatic pull toward the positively charged nucleus in the center of its circular orbit. This electrostatic pull is the centripetal force that causes the electron to move in a circle around the nucleus. Therefore, the magnitude of centripetal force is identified with the magnitude of the electrostatic force:
\[ \dfrac{m_ev_n^2}{r_n} = \dfrac{1}{4\pi \epsilon_0} \dfrac{e^2}{r_n^2}. \label{6.36} \]
Here, \(e\) denotes the value of the elementary charge. The negative electron and positive proton have the same value of charge,
\[|q| = e. \nonumber \]
When Equation \ref{6.36} is combined with the first quantization condition given by Equation \ref{6.34}, we can solve for the speed, \(v_n\), and for the radius, \(r_n\):
\[v_n = \dfrac{1}{4\pi \epsilon_0} \dfrac{e^2}{\hbar} \dfrac{1}{n} \label{6.37} \]
\[r_n = 4\pi \epsilon_0 \dfrac{\hbar^2}{m_ee^2}n^2. \label{6.38} \]
Note that these results tell us that the electron’s speed as well as the radius of its orbit depend only on the index n that enumerates the orbit because all other quantities in the preceding equations are fundamental constants. We see from Equation \ref{6.38} that the size of the orbit grows as the square of n. This means that the second orbit is four times as large as the first orbit, and the third orbit is nine times as large as the first orbit, and so on. We also see from Equation \ref{6.37} that the electron’s speed in the orbit decreases as the orbit size increases. The electron’s speed is largest in the first Bohr orbit, for \(n = 1\), which is the orbit closest to the nucleus. The radius of the first Bohr orbit is called the Bohr radius of hydrogen, denoted as \(a_0\). Its value is obtained by setting \(n = 1\) in Equation \ref{6.38}:
\[a_0 = 4\pi \epsilon_0 \dfrac{\hbar^2}{m_ee^2} = 5.29 \times 10^{-11} m = 0.529\space Å. \nonumber \]
We can substitute \(a_0\) in Equation \ref{6.38} to express the radius of the nth orbit in terms of \(a_0\):
\[r_n = a_0n^2. \label{6.40} \]
This result means that the electron orbits in hydrogen atom are quantized because the orbital radius takes on only specific values of \(a_0\), \(4a_0\), \(9a_0\), \(16a_0\)... given by Equation \ref{6.40}, and no other values are allowed.
Electron Energies
The total energy \(E_n\) of an electron in the nth orbit is the sum of its kinetic energy \(K_n\) and its electrostatic potential energy \(U_n\). Utilizing Equation \ref{6.37}, we find that
\[K_n = \dfrac{1}{2}m_ev_n^2 = \dfrac{1}{32\pi^2 \epsilon^2} \dfrac{m_ee^4}{\hbar^2} \dfrac{1}{n^2}. \label{6.41} \]
Recall that the electrostatic potential energy of interaction between two charges \(q_1\) and \(q_2\) that are separated by a distance \(r_{12}\) is \((1/4\pi \epsilon_0)q_1q_2/r_{12}\). Here, \(q_1 = +e\) is the charge of the nucleus in the hydrogen atom (the charge of the proton), \(q_2 = -e\) is the charge of the electron and \(r_{12} = r_n\) is the radius of the n-th orbit. Now we use Equation \ref{6.38} to find the potential energy of the electron:
\[U_n = - \dfrac{1}{4\pi \epsilon_0} \dfrac{e^2}{r_n} = - \dfrac{1}{16\pi^2 \epsilon_0^2} \dfrac{m_ee^4}{\hbar^2} \dfrac{1}{n^2}. \label{6.42} \]
The total energy of the electron is the sum of Equation \ref{6.41} and Equation \ref{6.42}:
\[E_n = K_n + U_n = - \dfrac{1}{32\pi^2 \epsilon_0^2} \dfrac{m_ee^4}{\hbar^2} \dfrac{1}{n^2}. \label{6.43} \]
Note that the energy depends only on the index n because the remaining symbols in Equation \ref{6.43} are physical constants. The value of the constant factor in Equation \ref{6.43} is
\[E_0 = \dfrac{1}{32\pi^2 \epsilon_0^2} \dfrac{m_ee^4}{\hbar^2} = \dfrac{1}{8\epsilon_0^2} \dfrac{m_ee^4}{h^2} = 2.17 \times 10^{-18} J = 13.6 \, eV. \label{6.44} \]
It is convenient to express the electron’s energy in the nth orbit in terms of this energy, as
\[E_n = -E_0 \dfrac{1}{n^2}. \label{6.45} \]
Now we can see that the electron energies in the hydrogen atom are quantized because they can have only discrete values of \(-E_0, \, -E_0/4, \, -E_0/9, \, -E_0/16, . . . \) given by Equation \ref{6.45}, and no other energy values are allowed. This set of allowed electron energies is called the energy spectrum of hydrogen (Figure \(\PageIndex{5}\)). The index n that enumerates energy levels in Bohr’s model is called the energy quantum number. We identify the energy of the electron inside the hydrogen atom with the energy of the hydrogen atom. Note that the smallest value of energy is obtained for \(n = 1\), so the hydrogen atom cannot have energy smaller than that. This smallest value of the electron energy in the hydrogen atom is called the ground state energy of the hydrogen atom and its value is
\[E_1 = −E_0 = −13.6 \, eV. \label{6.46} \]
The hydrogen atom may have other energies that are higher than the ground state. These higher energy states are known as excited energy states of a hydrogen atom.
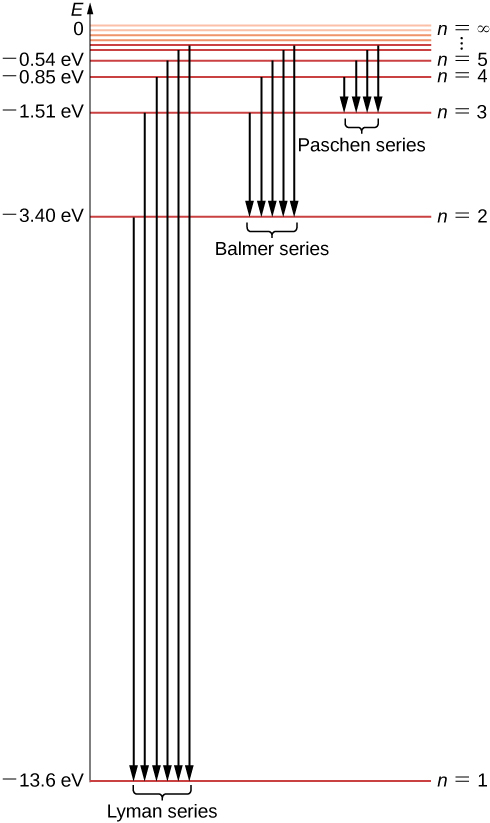
There is only one ground state, but there are infinitely many excited states because there are infinitely many values of n in Equation \ref{6.45}. We say that the electron is in the “first exited state” when its energy is \(E_n\) (when \(n = 2\)), the second excited state when its energy is \(E_3\) (when \(n = 3\)) and, in general, in the nth exited state when its energy is \(E_n + 1\). There is no highest-of-all excited state; however, there is a limit to the sequence of excited states. If we keep increasing \(n\) in Equation \ref{6.45}, we find that the limit is \(- lim_{n \rightarrow \infty} \, E_0/n^2 = 0\). In this limit, the electron is no longer bound to the nucleus but becomes a free electron. An electron remains bound in the hydrogen atom as long as its energy is negative. An electron that orbits the nucleus in the first Bohr orbit, closest to the nucleus, is in the ground state, where its energy has the smallest value. In the ground state, the electron is most strongly bound to the nucleus and its energy is given by Equation \ref{6.46}. If we want to remove this electron from the atom, we must supply it with enough energy, \(E_{\infty}\), to at least balance out its ground state energy \(E_1\):
\[E_{\infty} + E_1 = 0 \Rightarrow E_{\infty} = - E_1 = - (- E_0) = E_0 = 13.6 \, eV. \label{6.47} \]
The energy that is needed to remove the electron from the atom is called the ionization energy. The ionization energy \(E_{\infty}\) that is needed to remove the electron from the first Bohr orbit is called the ionization limit of the hydrogen atom. The ionization limit in Equation \ref{6.47} that we obtain in Bohr’s model agrees with experimental value.
Spectral Emission Lines of Hydrogen
To obtain the wavelengths of the emitted radiation when an electron makes a transition from the n-th orbit to the m-th orbit, we use the second of Bohr’s quantization conditions and Equation \ref{6.45} for energies. The emission of energy from the atom can occur only when an electron makes a transition from an excited state to a lower-energy state. In the course of such a transition, the emitted photon carries away the difference of energies between the states involved in the transition. The transition cannot go in the other direction because the energy of a photon cannot be negative, which means that for emission we must have \(E_n > E_m\) and \(n > m\). Therefore, the third of Bohr’s postulates gives
\[\begin{align} hf &= |E_n - E_m| \nonumber \\[4pt] &= E_n - E_m \nonumber \\[4pt] &= -E_0 \dfrac{1}{n^2} + E_m \dfrac{1}{m^2} \nonumber \\[4pt] &= E_0 \left( \dfrac{1}{m^2} - \dfrac{1}{n^2} \right). \label{6.48} \end{align} \]
Now we express the photon’s energy in terms of its wavelength, \(hf = hc/\lambda\), and divide both sides of Equation \ref{6.48} by \(hc\). The result is
\[ \dfrac{1}{\lambda} = \dfrac{E_0}{hc} \left( \dfrac{1}{m^2} - \dfrac{1}{n^2} \right). \label{6.49} \]
The value of the constant in this equation is
\[\dfrac{E_0}{hc} = \dfrac{13.6 \, eV}{(4.136 \times 10^{-15} eV \cdot s)(2.997 \times 10^8 m/s)} = 1.097 \times 10^7 \dfrac{1}{m}. \label{6.50} \]
This value is exactly the Rydberg constant \(R_H\) in the Rydberg heuristic formula Equation \ref{rydberg}. In fact, Equation \ref{6.49} is identical to the Rydberg formula, because for a given m, we have \(n = m + 1, \, m + 2, . . .\). In this way, the Bohr quantum model of the hydrogen atom allows us to derive the experimental Rydberg constant from first principles and to express it in terms of fundamental constants. Transitions between the allowed electron orbits are illustrated in Figure \(\PageIndex{5}\).
We can repeat the same steps that led to Equation \ref{6.49} to obtain the wavelength of the absorbed radiation; this again gives Equation \ref{6.49} but this time for the positions of absorption lines in the absorption spectrum of hydrogen. The only difference is that for absorption, the quantum number \(m\) is the index of the orbit occupied by the electron before the transition (lower-energy orbit) and the quantum number \(n\) is the index of the orbit to which the electron makes the transition (higher-energy orbit). The difference between the electron energies in these two orbits is the energy of the absorbed photon.
If a hydrogen atom in the ground state absorbs a 93.7-nm photon, corresponding to a transition line in the Lyman series, how does this affect the atom’s energy and size? How much energy is needed to ionize the atom when it is in this excited state? Give your answers in absolute units, and relative to the ground state.
Strategy
Before the absorption, the atom is in its ground state. This means that the electron transition takes place from the orbit \(m = 1\) to some higher nth orbit. First, we must determine nn for the absorbed wavelength \(\lambda = 93.7 \, nm\). Then, we can use Equation \ref{6.45} to find the energy \(E_n\) of the excited state and its ionization energy \(E_{\infty,n}\), and use Equation \ref{6.40} to find the radius \(r_n\) of the atom in the excited state. To estimate n, we use Equation \ref{6.49}.
Solution
Substitute \(m = 1\) and λ = 93.7 nm in Equation \ref{6.49} and solve for n. You should not expect to obtain a perfect integer answer because of rounding errors, but your answer will be close to an integer, and you can estimate n by taking the integral part of your answer:
\[ \begin{align*} \dfrac{1}{\lambda} &= R_H \left( \dfrac{1}{1^1} - \dfrac{1}{n^2}\right) \\[4pt] \Rightarrow n &= \dfrac{1}{\sqrt{1 - \dfrac{1}{\lambda R_H}}} \\[4pt] &= \dfrac{1}{\sqrt{1 - \dfrac{1}{(93.7 \times 10^{−9}m)(1.097 \times 10^7 m^{−1})}}} \\[4pt] &= 6.07 \\[4pt] \Rightarrow n &= 6. \end{align*} \]
The radius of the \(n = 6\) orbit is
\[r_n = a_0n^2= a_06^2 = 36a_0 = 36(0.529 \times 10^{−10} \, m) = 19.04 \times 10^{−10}\space m ≅ 19.0 \, Å. \nonumber \]
Thus, after absorbing the 93.7-nm photon, the size of the hydrogen atom in the excited \(n = 6\) state is 36 times larger than before the absorption, when the atom was in the ground state. The energy of the fifth excited state (\(n = 6\)) is:
\[E_n = - \dfrac{E_0}{n^2} = - \dfrac{E_0}{6^2} = - \dfrac{E_0}{36} = - \dfrac{13.6 \, eV}{36} ≅ − 0.378 \, eV. \nonumber \]
After absorbing the 93.7-nm photon, the energy of the hydrogen atom is larger than it was before the absorption. Ionization of the atom when it is in the fifth excited state (\(n = 6\)) requites 36 times less energy than is needed when the atom is in the ground state:
\[E_{\infty,6} = -E_6 = -(-0.378 \, eV) = 0.378 \, eV. \nonumber \]
Significance
We can analyze any spectral line in the spectrum of hydrogen in the same way. Thus, the experimental measurements of spectral lines provide us with information about the atomic structure of the hydrogen atom.
When an electron in a hydrogen atom is in the first excited state, what prediction does the Bohr model give about its orbital speed and kinetic energy? What is the magnitude of its orbital angular momentum?
- Answer
-
\(v_2 = 1.1 \times 10^6 m/s ≅0.0036 \, c;\)
\(L_2 = 2\hbar K_2 = 3.4 \, eV\)
Bohr’s model of the hydrogen atom also correctly predicts the spectra of some hydrogen-like ions. Hydrogen-like ions are atoms of elements with an atomic number Z larger than one (\(Z = 1\) for hydrogen) but with all electrons removed except one. For example, an electrically neutral helium atom has an atomic number \(Z = 2\). This means it has two electrons orbiting the nucleus with a charge of \(q = +Ze\). When one of the orbiting electrons is removed from the helium atom (we say, when the helium atom is singly ionized), what remains is a hydrogen-like atomic structure where the remaining electron orbits the nucleus with a charge of \(q = +Ze\). This type of situation is described by the Bohr model. Assuming that the charge of the nucleus is not \(+e\) but \(+Ze\), we can repeat all steps, beginning with Equation \ref{6.36}, to obtain the results for a hydrogen-like ion:
\[r_n = \dfrac{a_0}{Z}n^2 \label{6.51} \]
where \(a_0\) is the Bohr orbit of hydrogen, and
\[E_n = -Z^2E_0 \dfrac{1}{n^2} \label{6.52} \]
where \(E_0\) is the ionization limit of a hydrogen atom. These equations are good approximations as long as the atomic number Z is not too large.
The Bohr model is important because it was the first model to postulate the quantization of electron orbits in atoms. Thus, it represents an early quantum theory that gave a start to developing modern quantum theory. It introduced the concept of a quantum number to describe atomic states. The limitation of the early quantum theory is that it cannot describe atoms in which the number of electrons orbiting the nucleus is larger than one. The Bohr model of hydrogen is a semi-classical model because it combines the classical concept of electron orbits with the new concept of quantization. The remarkable success of this model prompted many physicists to seek an explanation for why such a model should work at all, and to seek an understanding of the physics behind the postulates of early quantum theory. This search brought about the onset of an entirely new concept of “matter waves.”


