1.A: The Nature of Light (Answers)
- Page ID
- 10326
Check Your Understanding
1.1. 2.1% (to two significant figures)
1.2. 15.1°
1.3. air to water, because the condition that the second medium must have a smaller index of refraction is not satisfied
1.4. 9.3 cm
1.5. \(\displaystyle AA'\) becomes longer, \(\displaystyle A'B'\) tilts further away from the surface, and the refracted ray tilts away from the normal.
1.6. also \(\displaystyle 90.0%\)
1.7. There will be only refraction but no reflection.
Conceptual Questions
1. model as a ray when devices are large compared to wavelength, as a wave when devices are comparable or small compared to wavelength
3. This fact simply proves that the speed of light is greater than that of sound. If one knows the distance to the location of the lightning and the speed of sound, one could, in principle, determine the speed of light from the data. In practice, because the speed of light is so great, the data would have to be known to impractically high precision.
5. Powder consists of many small particles with randomly oriented surfaces. This leads to diffuse reflection, reducing shine.
7. “toward” when increasing n (air to water, water to glass); “away” when decreasing n (glass to air)
9. A ray from a leg emerges from water after refraction. The observer in air perceives an apparent location for the source, as if a ray traveled in a straight line. See the dashed ray below.
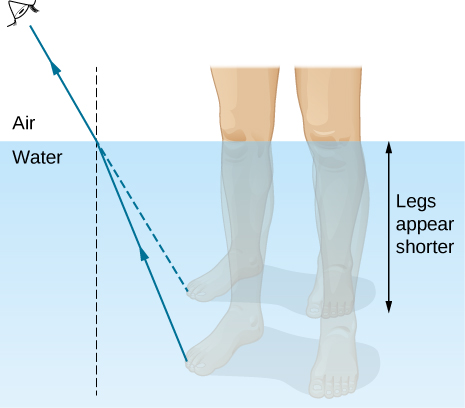
The figure is illustration of the formation of the image of a leg under water, as seen by a viewer in the air above the water. A ray is shown leaving the leg and refracting at the water air interface. The refracted ray bends away from the normal. Extrapolating the refracted ray back into the water, the extrapolated ray is above the actual ray so that the image of the leg is above the actual leg and the leg appears shorter.
11. The gemstone becomes invisible when its index of refraction is the same, or at least similar to, the water surrounding it. Because diamond has a particularly high index of refraction, it can still sparkle as a result of total internal reflection, not invisible.
13. One can measure the critical angle by looking for the onset of total internal reflection as the angle of incidence is varied. Equation 1.5 can then be applied to compute the index of refraction.
15. In addition to total internal reflection, rays that refract into and out of diamond crystals are subject to dispersion due to varying values of n across the spectrum, resulting in a sparkling display of colors.
17. yes
19. No. Sound waves are not transverse waves.
21. Energy is absorbed into the filters.
23. Sunsets are viewed with light traveling straight from the Sun toward us. When blue light is scattered out of this path, the remaining red light dominates the overall appearance of the setting Sun.
25. The axis of polarization for the sunglasses has been rotated \(\displaystyle 90°\).
Problems
27. \(\displaystyle 2.99705×10^8m/s; 1.97×10^8m/s\)
29. ice at \(\displaystyle 0°C\)
31. 1.03 ns
33. 337 m
35. proof
37. proof
39. reflection, \(\displaystyle 70°\); refraction, \(\displaystyle 45°\)
41. \(\displaystyle 42°\)
43. 1.53
45. a. 2.9 m;
b. 1.4 m
47. a. \(\displaystyle 24.42°\);
b. \(\displaystyle 31.33°\)
49. \(\displaystyle 79.11°\)
51. a. 1.43, fluorite;
b. \(\displaystyle 44.2°\)
53. a. \(\displaystyle 48.2°\);
b. \(\displaystyle 27.3°\)
55. \(\displaystyle 46.5°\) for red, \(\displaystyle 46.0°\) for violet
57. a. \(\displaystyle 0.04°\);
b. 1.3 m
59. \(\displaystyle 72.8°\)
61. \(\displaystyle 53.5°\) for red, \(\displaystyle 55.2°\) for violet
63. 0.500
65. 0.125 or 1/8
67. \(\displaystyle 84.3°\)
69. \(\displaystyle 0.250I_0\)
71. a. 0.500;
b. 0.250;
c. 0.187
73. \(\displaystyle 67.54°\)
75. \(\displaystyle 53.1°\)
Additional Problems
77. 114 radian/s
79. 3.72 mm
81. \(\displaystyle 41.2°\)
83. a. 1.92. The gem is not a diamond (it is zircon).
b. \(\displaystyle 55.2°\)
85. a. 0.898;
b. We cannot have \(\displaystyle n<1.00\), since this would imply a speed greater than c.
c. The refracted angle is too big relative to the angle of incidence.
87. \(\displaystyle 0.707B_1\)
89. a. \(\displaystyle 1.69×10^{−2}°C/s\);
b. yes
Challenge Problems
91. First part: \(\displaystyle 88.6°\). The remainder depends on the complexity of the solution the reader constructs.
93. proof; 1.33
95. a. 0.750;
b. 0.563;
c. 1.33


