8.2: The Hydrogen Atom
- Page ID
- 4534
By the end of this section, you will be able to:
- Describe the hydrogen atom in terms of wave function, probability density, total energy, and orbital angular momentum
- Identify the physical significance of each of the quantum numbers (n, l, m) of the hydrogen atom
- Distinguish between the Bohr and Schrödinger models of the atom
- Use quantum numbers to calculate important information about the hydrogen atom
The hydrogen atom is the simplest atom in nature and, therefore, a good starting point to study atoms and atomic structure. The hydrogen atom consists of a single negatively charged electron that moves about a positively charged proton (Figure \(\PageIndex{1}\)). In Bohr’s model, the electron is pulled around the proton in a perfectly circular orbit by an attractive Coulomb force. The proton is approximately 1800 times more massive than the electron, so the proton moves very little in response to the force on the proton by the electron. (This is analogous to the Earth-Sun system, where the Sun moves very little in response to the force exerted on it by Earth.) An explanation of this effect using Newton’s laws is given in Photons and Matter Waves.
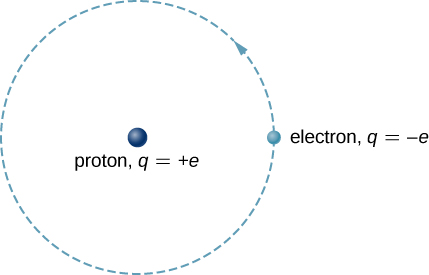
With the assumption of a fixed proton, we focus on the motion of the electron.
In the electric field of the proton, the potential energy of the electron is
\[U(r) = -k\frac{e^2}{r}, \nonumber \]
where \(k = 1/4\pi\epsilon_0\) and \(r\) is the distance between the electron and the proton. As we saw earlier, the force on an object is equal to the negative of the gradient (or slope) of the potential energy function. For the special case of a hydrogen atom, the force between the electron and proton is an attractive Coulomb force.
Notice that the potential energy function \(U(r)\) does not vary in time. As a result, Schrödinger’s equation of the hydrogen atom reduces to two simpler equations: one that depends only on space (x, y, z) and another that depends only on time (t). (The separation of a wave function into space- and time-dependent parts for time-independent potential energy functions is discussed in Quantum Mechanics.) We are most interested in the space-dependent equation:
\[\frac{-\hbar}{2m_e}\left(\frac{\partial^2\psi}{\partial x^2} + \frac{\partial^2\psi}{\partial y^2} + \frac{\partial^2\psi}{\partial z^2}\right) - k\frac{e^2}{r}\psi = E\psi, \nonumber \]
where \(\psi = psi (x,y,z)\) is the three-dimensional wave function of the electron, meme is the mass of the electron, and \(E\) is the total energy of the electron. Recall that the total wave function \(\Psi (x,y,z,t)\), is the product of the space-dependent wave function \(\psi = \psi(x,y,z)\) and the time-dependent wave function \(\varphi = \varphi(t)\).
In addition to being time-independent, \(U(r)\) is also spherically symmetrical. This suggests that we may solve Schrödinger’s equation more easily if we express it in terms of the spherical coordinates (\(r, \theta, \phi\)) instead of rectangular coordinates (\(x,y,z\)). A spherical coordinate system is shown in Figure \(\PageIndex{2}\). In spherical coordinates, the variable \(r\) is the radial coordinate, \(\theta\) is the polar angle (relative to the vertical z-axis), and \(\phi\) is the azimuthal angle (relative to the x-axis). The relationship between spherical and rectangular coordinates is \(x = r \, \sin \, \theta \, \cos \, \phi\), \(y = r \, \sin \theta \, \sin \, \phi\), \(z = r \, \cos \, \theta\).
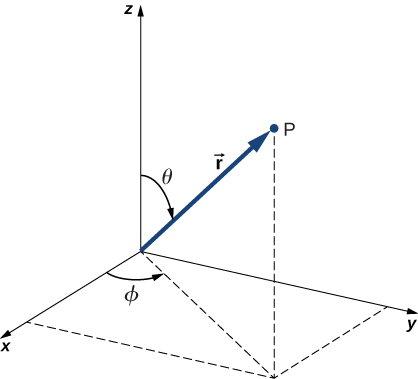
The factor \(r \, \sin \, \theta\) is the magnitude of a vector formed by the projection of the polar vector onto the xy-plane. Also, the coordinates of x and y are obtained by projecting this vector onto the x- and y-axes, respectively. The inverse transformation gives
\[\begin{align*} r &= \sqrt{x^2 + y^2 + z^2} \\[4pt] \theta &= \cos^{-1} \left(\frac{z}{r}\right), \\[4pt] \phi &= \cos^{-1} \left( \frac{x}{\sqrt{x^2 + y^2}}\right) \end{align*} \nonumber \]
Schrödinger’s wave equation for the hydrogen atom in spherical coordinates is discussed in more advanced courses in modern physics, so we do not consider it in detail here. However, due to the spherical symmetry of \(U(r)\), this equation reduces to three simpler equations: one for each of the three coordinates (\(r\), \(θ\), and \(ϕ\)). Solutions to the time-independent wave function are written as a product of three functions:
\[\psi (r, \theta, \phi) = R(r) \Theta(\theta) \Phi (\phi), \nonumber \]
where \(R\) is the radial function dependent on the radial coordinate \(r\) only; \(Θ\) is the polar function dependent on the polar coordinate \(θ\) only; and \(Φ\) is the phi function of \(ϕ\) only. Valid solutions to Schrödinger’s equation \(ψ(r, θ, ϕ)\) are labeled by the quantum numbers \(n\), \(l\), and \(m\).
- \(n\): principal quantum number
- \(l\): angular momentum quantum number
- \(m\): angular momentum projection quantum number
(The reasons for these names will be explained in the next section.) The radial function \(R\) depends only on \(n\) and \(l\); the polar function \(\Theta\) depends only on \(l\) and \(m\); and the phi function \(\Phi\) depends only on \(m\). The dependence of each function on quantum numbers is indicated with subscripts:
\[\psi_{nlm}(r, \theta, \phi) = R_{nl}(r)\Theta_{lm}(\theta)\Phi_m(\phi). \nonumber \]
Not all sets of quantum numbers (\(n\), \(l\), \(m\)) are possible. For example, the orbital angular quantum number \(l\) can never be greater or equal to the principal quantum number \(n(l < n)\). Specifically, we have
- \(n = 1,2,3,...\)
- \(l = 0,1,2,...,(n-1)\)
- \(m = -l, (-l+1), . . ., 0, . . ., (+l - 1), +l\)
Notice that for the ground state, \(n = 1\), \(l = 0\), and \(m = 0\). In other words, there is only one quantum state with the wave function for \(n = 1\), and it is \(\psi_{100}\). However, for \(n = 2\), we have
\[l = 0, \, m = 0 \nonumber \]
and
\[l = 1, \, m = -1, 0, 1. \nonumber \]
Therefore, the allowed states for the \(n = 2\) state are \(\psi_{200}\), \(\psi_{21-1}\), \(\psi_{210}\), and \(\psi_{211}\). Example wave functions for the hydrogen atom are given in Table \(\PageIndex{1}\). Note that some of these expressions contain the letter \(i\), which represents \(\sqrt{-1}\). When probabilities are calculated, these complex numbers do not appear in the final answer.
| \(n = 1, \, l = 0, \, m_l = 0\) | \(\displaystyle \psi_{100} = \frac{1}{\sqrt{\pi}} \frac{1}{a_0^{3/2}}e^{-r/a_0}\) |
| \(n = 2, \, l = 0, \, m_l = 0\) | \(\displaystyle\psi_{200} = \frac{1}{4\sqrt{2\pi}} \frac{1}{a_0^{3/2}}(2 - \frac{r}{a_0})e^{-r/2a_0}\) |
| \(n = 2, \, l = 1, \, m_l = -1\) | \(\displaystyle\psi_{21-1} = \frac{1}{8\sqrt{\pi}} \frac{1}{a_0^{3/2}}\frac{r}{a_0}e^{-r/2a_0}\sin \, \theta e^{-i\phi}\) |
| \(n = 2, \, l = 1, \, m_l = 0\) | \( \displaystyle \psi_{210} = \frac{1}{4\sqrt{2\pi}} \frac{1}{a_0^{3/2}}\frac{r}{a_0}e^{-r/2a_0}\cos \, \theta\) |
| \(n = 2, \, l = 1, \, m_l = 1\) | \( \displaystyle\psi_{211} = \frac{1}{8\sqrt{\pi}} \frac{1}{a_0^{3/2}}\frac{r}{a_0}e^{-r/2a_0}\sin \, \theta e^{i\phi}\) |
Physical Significance of the Quantum Numbers
Each of the three quantum numbers of the hydrogen atom (\(n\), \(l\), \(m\)) is associated with a different physical quantity.
Principal Quantum Number
The principal quantum number \(n\) is associated with the total energy of the electron, \(E_n\). According to Schrödinger’s equation:
\[E_n = - \left(\frac{m_ek^2e^4}{2\hbar^2}\right)\left(\frac{1}{n^2}\right) = - E_0 \left(\frac{1}{n^2}\right), \label{8.3} \]
where \(E_0 = -13.6 \, eV\). Notice that this expression is identical to that of Bohr’s model. As in the Bohr model, the electron in a particular state of energy does not radiate.
For the hydrogen atom, how many possible quantum states correspond to the principal number \(n = 3\)? What are the energies of these states?
Strategy
For a hydrogen atom of a given energy, the number of allowed states depends on its orbital angular momentum. We can count these states for each value of the principal quantum number, \(n = 1,2,3\). However, the total energy depends on the principal quantum number only, which means that we can use Equation \ref{8.3} and the number of states counted.
Solution
If \(n = 3\), the allowed values of \(l\) are 0, 1, and 2. If \(l = 0\), \(m = 0\) (1 state). If \(l = 1\), \(m = -1, 0, 1\) (3 states); and if \(l = 2\), \(m = -2, -1, 0, 1, 2\) (5 states). In total, there are 1 + 3 + 5 = 9 allowed states. Because the total energy depends only on the principal quantum number, \(n = 3\), the energy of each of these states is
\[E_{n3} = -E_0 \left(\frac{1}{n^2}\right) = \frac{-13.6 \, eV}{9} = - 1.51 \, eV. \nonumber \]
Significance
An electron in a hydrogen atom can occupy many different angular momentum states with the very same energy. As the orbital angular momentum increases, the number of the allowed states with the same energy increases.
Angular Momentum Orbital Quantum Number
The angular momentum orbital quantum number \(l\) is associated with the orbital angular momentum of the electron in a hydrogen atom. Quantum theory tells us that when the hydrogen atom is in the state \(\psi_{nlm}\), the magnitude of its orbital angular momentum is
\[L = \sqrt{l(l + 1)}\hbar, \nonumber \]
where \(l = 0, 1, 2, . . . , (n - 1)\).
This result is slightly different from that found with Bohr’s theory, which quantizes angular momentum according to the rule \(L = n\), where \(n = 1,2,3, ...\)
Quantum states with different values of orbital angular momentum are distinguished using spectroscopic notation (Table \(\PageIndex{2}\)). The designations s, p, d, and f result from early historical attempts to classify atomic spectral lines. (The letters stand for sharp, principal, diffuse, and fundamental, respectively.) After f, the letters continue alphabetically.
The ground state of hydrogen is designated as the 1s state, where “1” indicates the energy level (\(n = 1\)) and “s” indicates the orbital angular momentum state (\(l = 0\)). When \(n = 2\), \(l\) can be either 0 or 1. The \(n = 2\), \(l = 0\) state is designated “2s.” The \(n = 2\), \(l = 1\) state is designated “2p.” When \(n = 3\), \(l\) can be 0, 1, or 2, and the states are 3s, 3p, and 3d, respectively. Notation for other quantum states is given in Table \(\PageIndex{3}\).
| Orbital Quantum Number \(l\) | Angular Momentum | State | Spectroscopic Name |
|---|---|---|---|
| 0 | 0 | s | Sharp |
| 1 | \(\sqrt{2}h\) | p | Principal |
| 2 | \(\sqrt{6}h\) | d | Diffuse |
| 3 | \(\sqrt{12}h\) | f | Fundamental |
| 4 | \(\sqrt{20}h\) | g | |
| 5 | \(\sqrt{30}h\) | h |
Angular Momentum Projection Quantum Number
The angular momentum projection quantum number \(m\) is associated with the azimuthal angle \(\phi\) (see Figure \(\PageIndex{2}\)) and is related to the z-component of orbital angular momentum of an electron in a hydrogen atom. This component is given by
\[L_z = m\hbar, \nonumber \]
where \(m = -l, -l + 1, ..., 0, ..., +l - 1, l\).
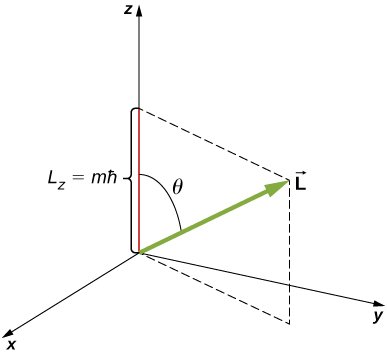
The z-component of angular momentum is related to the magnitude of angular momentum by
\[L_z = L \, \cos \theta, \nonumber \]
where \(\theta\) is the angle between the angular momentum vector and the z-axis. Note that the direction of the z-axis is determined by experiment - that is, along any direction, the experimenter decides to measure the angular momentum. For example, the z-direction might correspond to the direction of an external magnetic field. The relationship between \(L_z\) and \(L\) is given in Figure \(\PageIndex{3}\).
| \(l = 0\) | \(l = 1\) | \(l = 2\) | \(l = 3\) | \(l = 4\) | \(l = 5\) | |
| \(n = 1\) | 1s | |||||
| \(n = 2\) | 2s | 2p | ||||
| \(n = 3\) | 3s | 3p | 3d | |||
| \(n = 4\) | 4s | 4p | 4d | 4f | ||
| \(n = 5\) | 5s | 5p | 5d | 5f | 5g | |
| \(n = 6\) | 6s | 6p | 6d | 6f | 6g | 6h |
The quantization of \(L_z\) is equivalent to the quantization of \(\theta\). Substituting \(\sqrt{l(l + 1)}\hbar\) for \(L\) and \(m\) for \(L_z\) into this equation, we find
\[m\hbar = \sqrt{l(l + 1)}\hbar \, \cos \, \theta. \nonumber \]
Thus, the angle \(\theta\) is quantized with the particular values
\[\theta = \cos^{-1}\left(\frac{m}{\sqrt{l(l + 1)}}\right). \nonumber \]
Notice that both the polar angle (\(θ\)) and the projection of the angular momentum vector onto an arbitrary z-axis (\(L_z\)) are quantized.
The quantization of the polar angle for the \(l = 3\) state is shown in Figure \(\PageIndex{4}\). The orbital angular momentum vector lies somewhere on the surface of a cone with an opening angle \(\theta\) relative to the z-axis (unless \(m = 0\), in which case \(θ = 90^o\) and the vector points are perpendicular to the z-axis).
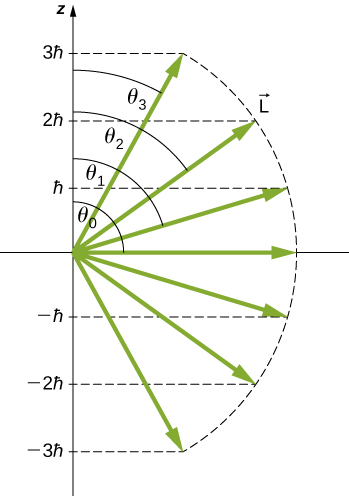
A detailed study of angular momentum reveals that we cannot know all three components simultaneously. In the previous section, the z-component of orbital angular momentum has definite values that depend on the quantum number \(m\). This implies that we cannot know both x- and y-components of angular momentum, \(L_x\) and \(L_y\), with certainty. As a result, the precise direction of the orbital angular momentum vector is unknown.
Calculate the angles that the angular momentum vector \(\vec{L}\) can make with the z-axis for \(l = 1\), as shown in Figure \(\PageIndex{5}\).
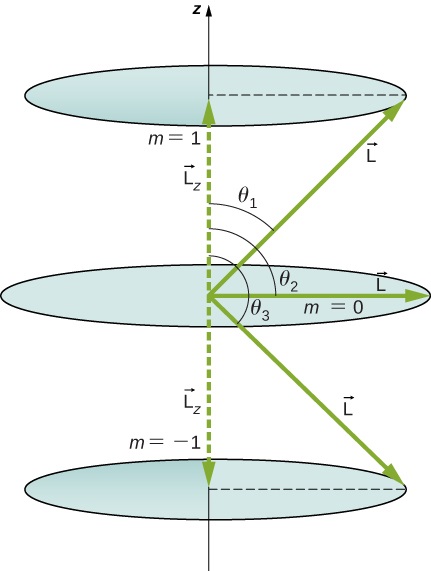
Strategy
The vectors \(\vec{L}\) and \(\vec{L_z}\) (in the z-direction) form a right triangle, where \(\vec{L}\) is the hypotenuse and \(\vec{L_z}\) is the adjacent side. The ratio of \(L_z\) to |\(\vec{L}\)| is the cosine of the angle of interest. The magnitudes \(L = |\vec{L}|\) and \(L_z\) are given by
\[L = \sqrt{l(l + 1)} \hbar \nonumber \]
and
\[L_z = m\hbar. \nonumber \]
Solution
We are given \(l = 1\), so \(m\) can be +1, 0, or +1. Thus, \(L\) has the value given by
\[L = \sqrt{l(l + 1)}\hbar = \sqrt{2}\hbar. \nonumber \]
The quantity \(L_z\) can have three values, given by \(L_z = m_l\hbar\).
\[L_z = \begin{cases} \hbar, & \text{if } m_l=+1 \\ 0, & \text{if } m_l=0 \\ \hbar, & \text{if } m_l=-1 \end{cases} \nonumber \]
As you can see in Figure \(\PageIndex{5}\), \(\cosθ=Lz/L\), so for \(m=+1\), we have
\[\cos \, \theta_1 = \frac{L_z}{L} = \frac{\hbar}{\sqrt{2}\hbar} = \frac{1}{\sqrt{2}} = 0.707 \nonumber \]
Thus,
\[\theta_1 = \cos^{-1}0.707 = 45.0°. \nonumber \]
Similarly, for \(m = 0\), we find \(\cos \, \theta_2 = 0\); this gives
\[\theta_2 = \cos^{-1}0 = 90.0°. \nonumber \]
Then for \(m_l = -1\):
\[\cos \, \theta_3 = \frac{L_Z}{L} = \frac{-\hbar}{\sqrt{2}\hbar} = -\frac{1}{\sqrt{2}} = -0.707, \nonumber \]
so that
\[\theta_3 = \cos^{-1}(-0.707) = 135.0°. \nonumber \]
Significance
The angles are consistent with the figure. Only the angle relative to the z-axis is quantized. \(L\) can point in any direction as long as it makes the proper angle with the z-axis. Thus, the angular momentum vectors lie on cones, as illustrated. To see how the correspondence principle holds here, consider that the smallest angle (\(\theta_1\) in the example) is for the maximum value of \(m_l\), namely \(m_l = l\). For that smallest angle,
\[\cos \, \theta = \dfrac{L_z}{L} = \dfrac{l}{\sqrt{l(l + 1)}}, \nonumber \]
which approaches 1 as \(l\) becomes very large. If \(cos \, \theta = 1\), then \(\theta = 0º\). Furthermore, for large \(l\), there are many values of \(m_l\), so that all angles become possible as \(l\) gets very large.
Can the magnitude \(L_z\) ever be equal to \(L\)?
- Answer
-
No. The quantum number \(m = -l, -l + l, ..., 0, ..., l -1, l\). Thus, the magnitude of \(L_z\) is always less than \(L\) because \(<\sqrt{l(l + 1)}\)
Using the Wave Function to Make Predictions
As we saw earlier, we can use quantum mechanics to make predictions about physical events by the use of probability statements. It is therefore proper to state, “An electron is located within this volume with this probability at this time,” but not, “An electron is located at the position (x, y, z) at this time.” To determine the probability of finding an electron in a hydrogen atom in a particular region of space, it is necessary to integrate the probability density \(|ψ_{nlm}|^2)_ over that region:
\[\text{Probability} = \int_{volume} |\psi_{nlm}|^2 dV, \nonumber \]
where \(dV\) is an infinitesimal volume element. If this integral is computed for all space, the result is 1, because the probability of the particle to be located somewhere is 100% (the normalization condition). In a more advanced course on modern physics, you will find that \(|\psi_{nlm}|^2 = \psi_{nlm}^* \psi_{nlm}\), where \(\psi_{nlm}^*\) is the complex conjugate. This eliminates the occurrences \(i = \sqrt{-1}\) in the above calculation.
Consider an electron in a state of zero angular momentum (\(l = 0\)). In this case, the electron’s wave function depends only on the radial coordinate \(r\). (Refer to the states \(\psi_{100}\) and \(\psi_{200}\) in Table \(\PageIndex{1}\).) The infinitesimal volume element corresponds to a spherical shell of radius \(r\) and infinitesimal thickness \(dr\), written as
\[dV = 4\pi r^2dr. \nonumber \]
The probability of finding the electron in the region \(r\) to \(r + dr\) (“at approximately r”) is
\[P(r)dr = |\psi_{n00}|^2 4\pi r^2 dr. \nonumber \]
Here \(P(r)\) is called the radial probability density function (a probability per unit length). For an electron in the ground state of hydrogen, the probability of finding an electron in the region \(r\) to \(r + dr\) is
\[|\psi_{n00}|^2 4\pi r^2 dr = (4/a_)^3)r^2 exp(-2r/a_0)dr, \nonumber \]
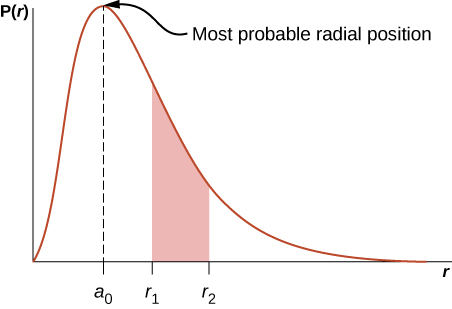
where \(a_0 = 0.5\) angstroms. The radial probability density function \(P(r)\) is plotted in Figure \(\PageIndex{6}\). The area under the curve between any two radial positions, say \(r_1\) and \(r_2\), gives the probability of finding the electron in that radial range. To find the most probable radial position, we set the first derivative of this function to zero (\(dP/dr = 0\)) and solve for \(r\). The most probable radial position is not equal to the average or expectation value of the radial position because \(|\psi_{n00}|^2\) is not symmetrical about its peak value.
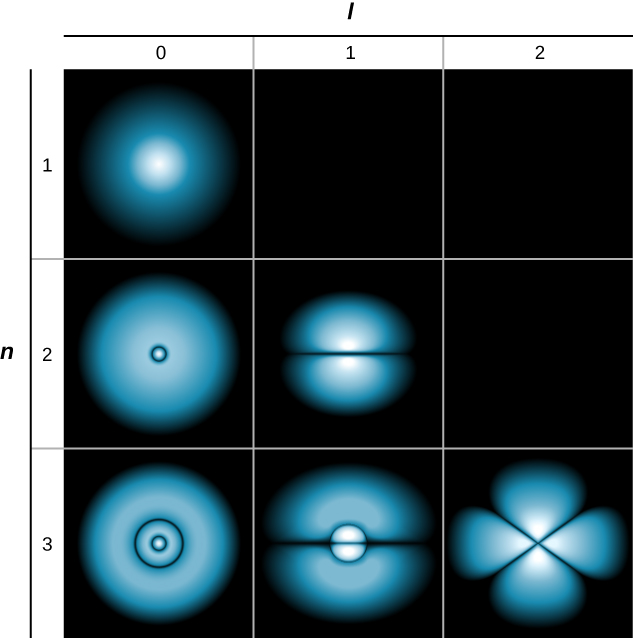
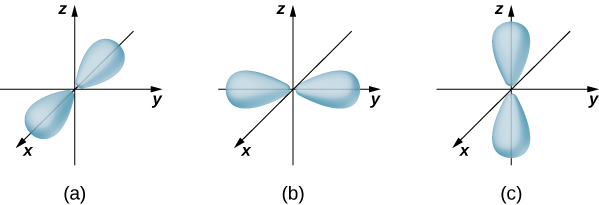
If the electron has orbital angular momentum (\(l \neq 0\)), then the wave functions representing the electron depend on the angles \(\theta\) and \(\phi\); that is, \(\psi_{nlm} = \psi_{nlm}(r, \theta, \phi)\). Atomic orbitals for three states with \(n = 2\) and \(l = 1\) are shown in Figure \(\PageIndex{7}\). An atomic orbital is a region in space that encloses a certain percentage (usually 90%) of the electron probability. (Sometimes atomic orbitals are referred to as “clouds” of probability.) Notice that these distributions are pronounced in certain directions. This directionality is important to chemists when they analyze how atoms are bound together to form molecules.
A slightly different representation of the wave function is given in Figure \(\PageIndex{8}\). In this case, light and dark regions indicate locations of relatively high and low probability, respectively. In contrast to the Bohr model of the hydrogen atom, the electron does not move around the proton nucleus in a well-defined path. Indeed, the uncertainty principle makes it impossible to know how the electron gets from one place to another.