9.9: Superconductivity
- Page ID
- 4940
By the end of this section, you will be able to:
- Describe the main features of a superconductor
- Describe the BCS theory of superconductivity
- Determine the critical magnetic field for T = 0 K from magnetic field data
- Calculate the maximum emf or current for a wire to remain superconducting
Electrical resistance can be considered as a measure of the frictional force in electrical current flow. Thus, electrical resistance is a primary source of energy dissipation in electrical systems such as electromagnets, electric motors, and transmission lines. Copper wire is commonly used in electrical wiring because it has one of the lowest room-temperature electrical resistivities among common conductors. (Actually, silver has a lower resistivity than copper, but the high cost and limited availability of silver outweigh its savings in energy over copper.)
Although our discussion of conductivity seems to imply that all materials must have electrical resistance, we know that this is not the case. When the temperature decreases below a critical value for many materials, their electrical resistivity drops to zero, and the materials become superconductors.
Watch this NOVA video excerpt, Making Stuff Colder, as an introduction to the topic of superconductivity and its many applications.
Properties of Superconductors
In addition to zero electrical resistance, superconductors also have perfect diamagnetism. In other words, in the presence of an applied magnetic field, the net magnetic field within a superconductor is always zero (Figure \(\PageIndex{1}\)). Therefore, any magnetic field lines that pass through a superconducting sample when it is in its normal state are expelled once the sample becomes superconducting. These are manifestations of the Meissner effect, which you learned about in the chapter on current and resistance.
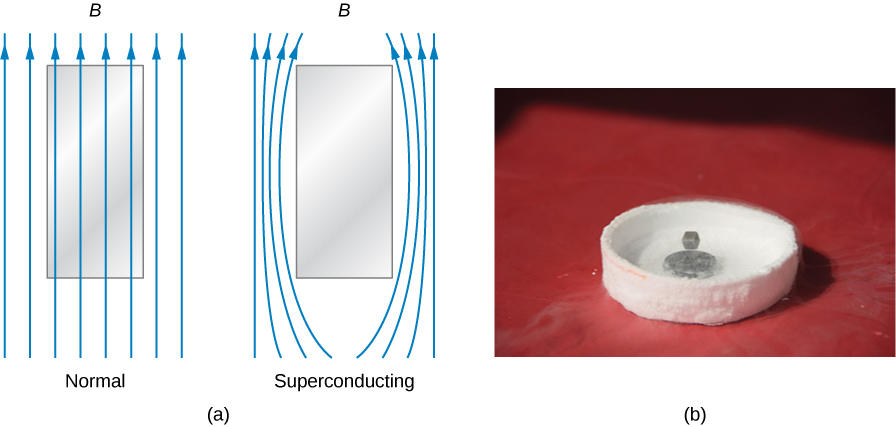
Interestingly, the Meissner effect is not a consequence of the resistance being zero. To see why, suppose that a sample placed in a magnetic field undergoes a transition in which its resistance drops to zero. From Ohm’s law, the current density, j, in the sample is related to the net internal electric field, E, and the resistivity \(\rho\) by \(j = E/\rho\) If \(\rho\) is zero, E must also be zero so that j can remain finite. Now E and the magnetic flux \(\Phi_m\) through the sample are related by Faraday’s law as
\[\oint E\,dI = - \dfrac{d\Phi_m}{dt} \nonumber \]
If E is zero, \(d\Phi_m/dt\) is also zero, that is, the magnetic flux through the sample cannot change. The magnetic field lines within the sample should therefore not be expelled when the transition occurs. Hence, it does not follow that a material whose resistance goes to zero has to exhibit the Meissner effect. Rather, the Meissner effect is a special property of superconductors.
Another important property of a superconducting material is its critical temperature, \(T_c\), the temperature below which the material is superconducting. The known range of critical temperatures is from a fraction of 1 K to slightly above 100 K. Superconductors with critical temperatures near this higher limit are commonly known as “high-temperature” superconductors. From a practical standpoint, superconductors for which \(T_c \gg 77 \, K\) are very important. At present, applications involving superconductors often still require that superconducting materials be immersed in liquid helium (4.2 K) in order to keep them below their critical temperature. The liquid helium baths must be continually replenished because of evaporation, and cooling costs can easily outweigh the savings in using a superconductor. However, 77 K is the temperature of liquid nitrogen, which is far more abundant and inexpensive than liquid helium. It would be much more cost-effective if we could easily fabricate and use high-temperature superconductor components that only need to be kept in liquid nitrogen baths to maintain their superconductivity.
High-temperature superconducting materials are presently in use in various applications. An example is the production of magnetic fields in some particle accelerators. The ultimate goal is to discover materials that are superconducting at room temperature. Without any cooling requirements, the bulk of electronic components and transmission lines could be superconducting, resulting in dramatic and unprecedented increases in efficiency and performance.
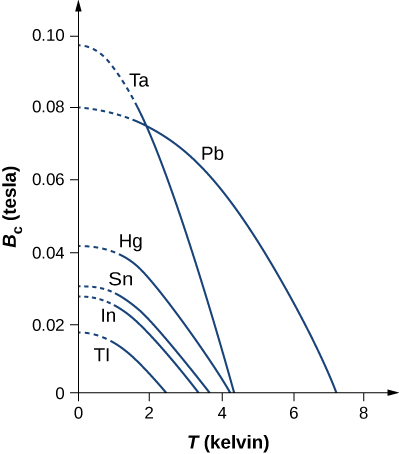
Another important property of a superconducting material is its critical magnetic field \(B_c(T)\), which is the maximum applied magnetic field at a temperature T that will allow a material to remain superconducting. An applied field that is greater than the critical field will destroy the superconductivity. The critical field is zero at the critical temperature and increases as the temperature decreases. Plots of the critical field versus temperature for several superconducting materials are shown in Figure \(\PageIndex{2}\) . The temperature dependence of the critical field can be described approximately by
\[B_c(T) = B_c(0) \left[1 - \left(\frac{T}{T_c}\right)^2\right] \nonumber \]
where \(B_0\) is the critical field at absolute zero temperature. Table \(\PageIndex{1}\) lists the critical temperatures and fields for two classes of superconductors: type I superconductor and type II superconductor. In general, type I superconductors are elements, such as aluminum and mercury. They are perfectly diamagnetic below a critical field BC(T), and enter the normal non-superconducting state once that field is exceeded. The critical fields of type I superconductors are generally quite low (well below one tesla). For this reason, they cannot be used in applications requiring the production of high magnetic fields, which would destroy their superconducting state.
| Material | Critical Temperature (K) | Critical Magnetic Field (T) |
|---|---|---|
| Type I | ||
| Al | 1.2 | 0.011 |
| Ga | 1.1 | 0.0051 |
| \(Hg(\alpha)\) | 4.2 | 0.041 |
| In | 3.4 | 0.029 |
| Nb | 9.3 | 0.20 |
| Pb | 7.2 | 0.080 |
| Sn | 3.7 | 0.031 |
| Th | 1.4 | 0.00016 |
| Zn | 0.87 | 0.0053 |
| Type II | ||
| \(Nb_3Al\) | 18 | 32 |
| \(Nb_3Ge\) | 23 | 38 |
| \(Nb_3Sn\) | 18 | 25 |
| \(NbTi\) | 9.3 | 15 |
| \(YBa_2Cu_3O_7\) | 92 | >100 |
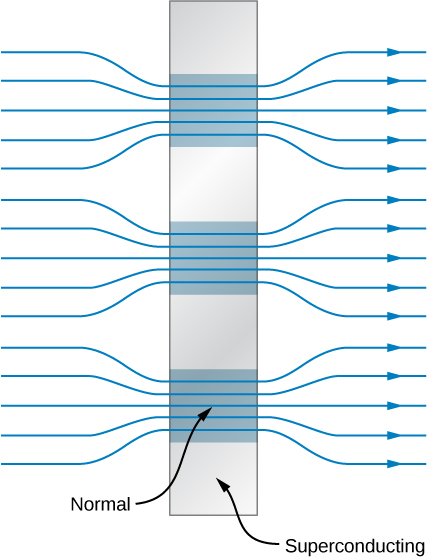
Type II superconductors are generally compounds or alloys involving transition metals or actinide series elements. Almost all superconductors with relatively high critical temperatures are type II. They have two critical fields, represented by \(B_{c1}(T)\) and \(B_{c2}(T)\). When the field is below \(B_{c1}(T)\), type II superconductors are perfectly diamagnetic, and no magnetic flux penetration into the material can occur. For a field exceeding \(B_{c2}(T)\), they are driven into their normal state. When the field is greater than \(B_{c1}(T)\) but less than \(B_{c2}(T)\),type II superconductors are said to be in a mixed state. Although there is some magnetic flux penetration in the mixed state, the resistance of the material is zero. Within the superconductor, filament-like regions exist that have normal electrical and magnetic properties interspersed between regions that are superconducting with perfect diamagnetism. A representation of this state is given in Figure \(\PageIndex{3}\). The magnetic field is expelled from the superconducting regions but exists in the normal regions. In general, \(B_{c2}(T)\) is very large compared with the critical fields of type I superconductors, so wire made of type II superconducting material is suitable for the windings of high-field magnets.
In an experiment, a niobium (Nb) wire of radius 0.25 mm is immersed in liquid helium \(T = 4.2 \, K)\) and required to carry a current of 300 A. Does the wire remain superconducting?
Strategy
The applied magnetic field can be determined from the radius of the wire and current. The critical magnetic field can be determined from [link], the properties of the superconductor, and the temperature. If the applied magnetic field is greater than the critical field, then superconductivity in the Nb wire is destroyed.
Solution
At \(T = 4.2 \, K\), the critical field for Nb is, from Table \(\PageIndex{1}\):
\[B_c(4.2 \, K) = B_c(0)\left[1 - \left(\frac{4.2 \, K}{9.3 \, K}\right)^2\right] = (0.20 \, T)(0.80) = 0.16 \, T. \nonumber \]
In an earlier chapter, we learned the magnetic field inside a current-carrying wire of radius \(a\) is given by
\[B = \frac{\mu_0I}{2\pi a}, \nonumber \]
where r is the distance from the central axis of the wire. Thus, the field at the surface of the wire is \(\frac{\mu_0I}{2\pi a}\). For the niobium wire, this field is
\[B = \frac{(4\pi \times 10^{-7} T m/A)(300 \, A)}{2\pi(2.5 \times 10^{-4}m)} = 0.24 \, T. \nonumber \]
Since this exceeds the critical 0.16 T, the wire does not remain superconducting.
Significance
Superconductivity requires low temperatures and low magnetic fields. These simultaneous conditions are met less easily for Nb than for many other metals. For example, aluminum superconducts at temperatures 7 times lower and magnetic fields 18 times lower.
What conditions are necessary for superconductivity?
- Answer
-
a low temperature and low magnetic field
Theory of Superconductors
A successful theory of superconductivity was developed in the 1950s by John Bardeen, Leon Cooper, and J. Robert Schrieffer, for which they received the Nobel Prize in 1972. This theory is known as the BCS theory. BCS theory is complex, so we summarize it qualitatively below.
In a normal conductor, the electrical properties of the material are due to the most energetic electrons near the Fermi energy. In 1956, Cooper showed that if there is any attractive interaction between two electrons at the Fermi level, then the electrons can form a bound state in which their total energy is less than 2EF2EF. Two such electrons are known as a Cooper pair.
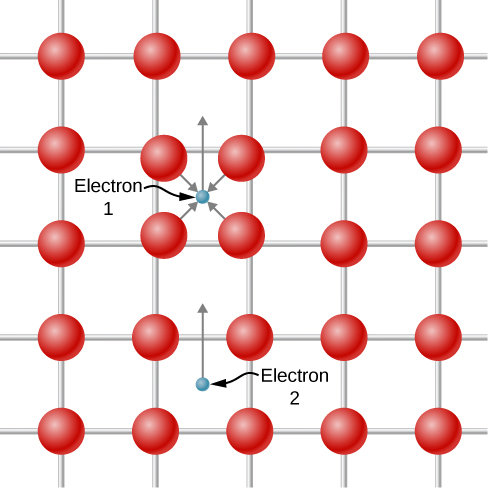
It is hard to imagine two electrons attracting each other, since they have like charge and should repel. However, the proposed interaction occurs only in the context of an atomic lattice. A depiction of the attraction is shown in Figure \(\PageIndex{4}\). Electron 1 slightly displaces the positively charged atomic nuclei toward itself as it travels past because of the Coulomb attraction. Electron 2 “sees” a region with a higher density of positive charge relative to the surroundings and is therefore attracted into this region and, therefore indirectly, to electron 1. Because of the exclusion principle, the two electrons of a Cooper pair must have opposite spin.
The BCS theory extends Cooper’s ideas, which are for a single pair of electrons, to the entire free electron gas. When the transition to the superconducting state occurs, all the electrons pair up to form Cooper pairs. On an atomic scale, the distance between the two electrons making up a Cooper pair is quite large. Between these electrons are typically about \(10^6\) other electrons, each also pairs with a distant electron. Hence, there is considerable overlap between the wave functions of the individual Cooper pairs, resulting in a strong correlation among the motions of the pairs. They all move together “in step,” like the members of a marching band. In the superconducting transition, the density of states becomes drastically changed near the Fermi level. As shown in Figure \(\PageIndex{5}\), an energy gap appears around \(E_F\) because the collection of Cooper pairs has lower ground state energy than the Fermi gas of noninteracting electrons. The appearance of this gap characterizes the superconducting state. If this state is destroyed, then the gap disappears, and the density of states reverts to that of the free electron gas.
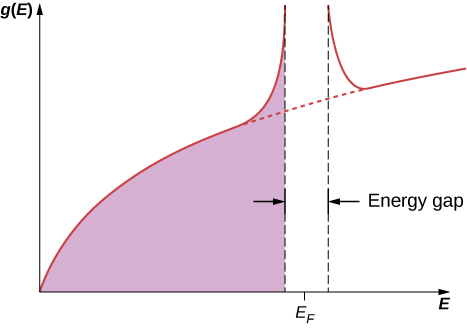
The BCS theory is able to predict many of the properties observed in superconductors. Examples include the Meissner effect, the critical temperature, the critical field, and, perhaps most importantly, the resistivity becoming zero at a critical temperature. We can think about this last phenomenon qualitatively as follows. In a normal conductor, resistivity results from the interaction of the conduction electrons with the lattice. In this interaction, the energy exchanged is on the order of \(k_BT\), the thermal energy. In a superconductor, electric current is carried by the Cooper pairs. The only way for a lattice to scatter a Cooper pair is to break it up. The destruction of one pair then destroys the collective motion of all the pairs. This destruction requires energy on the order of \(10^{-3}eV\), which is the size of the energy gap. Below the critical temperature, there is not enough thermal energy available for this process, so the Cooper pairs travel unimpeded throughout the superconductor.
Finally, it is interesting to note that no evidence of superconductivity has been found in the best normal conductors, such as copper and silver. This is not unexpected, given the BCS theory. The basis for the formation of the superconducting state is an interaction between the electrons and the lattice. In the best conductors, the electron-lattice interaction is weakest, as evident from their minimal resistivity. We might expect then that in these materials, the interaction is so weak that Cooper pairs cannot be formed, and superconductivity is therefore precluded.


