14.3: Self-Inductance and Inductors
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Correlate the rate of change of current to the induced emf created by that current in the same circuit
- Derive the self-inductance for a cylindrical solenoid
- Derive the self-inductance for a rectangular toroid
Mutual inductance arises when a current in one circuit produces a changing magnetic field that induces an emf in another circuit. But can the magnetic field affect the current in the original circuit that produced the field? The answer is yes, and this is the phenomenon called self-inductance.
Inductors
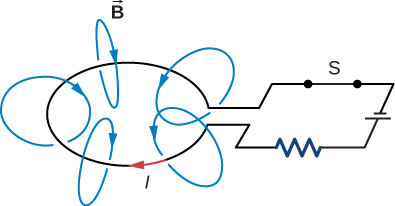
Figure 14.3.1 shows some of the magnetic field lines due to the current in a circular loop of wire. If the current is constant, the magnetic flux through the loop is also constant. However, if the current I were to vary with time—say, immediately after switch S is closed—then the magnetic flux Φm would correspondingly change. Then Faraday’s law tells us that an emf ϵ would be induced in the circuit, where
ϵ=−dΦmdt.
Since the magnetic field due to a current-carrying wire is directly proportional to the current, the flux due to this field is also proportional to the current; that is,
Φm∝I.
This can also be written as
Φm=LI
where the constant of proportionality L is known as the self-inductance of the wire loop. If the loop has N turns, this equation becomes
NΦm=LI
By convention, the positive sense of the normal to the loop is related to the current by the right-hand rule, so in Figure 14.3.1, the normal points downward. With this convention, Φm is positive in Equation ???, so L always has a positive value.
For a loop with N turns, ϵ=−NdΦm/dt, so the induced emf may be written in terms of the self-inductance as
ϵ=−LdIdt.
When using this equation to determine L, it is easiest to ignore the signs of ϵ and dI/dt, and calculate L as
L=|ϵ||dI/dt|.
Since self-inductance is associated with the magnetic field produced by a current, any configuration of conductors possesses self-inductance. For example, besides the wire loop, a long, straight wire has self-inductance, as does a coaxial cable. A coaxial cable is most commonly used by the cable television industry and may also be found connecting to your cable modem. Coaxial cables are used due to their ability to transmit electrical signals with minimal distortions. Coaxial cables have two long cylindrical conductors that possess current and a self-inductance that may have undesirable effects.

A circuit element used to provide self-inductance is known as an inductor. It is represented by the symbol shown in Figure 14.3.2, which resembles a coil of wire, the basic form of the inductor. Figure 14.3.3 shows several types of inductors commonly used in circuits.

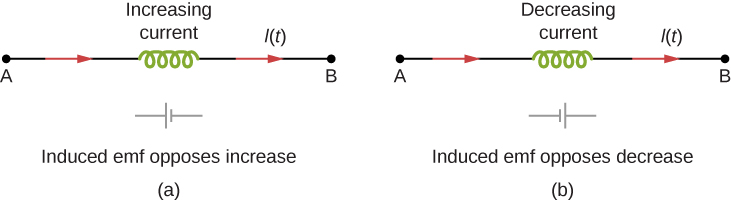
In accordance with Lenz’s law, the negative sign in Equation ??? indicates that the induced emf across an inductor always has a polarity that opposes the change in the current. For example, if the current flowing from A to B in Figure 14.3.4a were increasing, the induced emf (represented by the imaginary battery) would have the polarity shown in order to oppose the increase. If the current from A to B were decreasing, then the induced emf would have the opposite polarity, again to oppose the change in current (Figure 14.3.4b). Finally, if the current through the inductor were constant, no emf would be induced in the coil.
One common application of inductance is to allow traffic signals to sense when vehicles are waiting at a street intersection. An electrical circuit with an inductor is placed in the road underneath the location where a waiting car will stop. The body of the car increases the inductance and the circuit changes, sending a signal to the traffic lights to change colors. Similarly, metal detectors used for airport security employ the same technique. A coil or inductor in the metal detector frame acts as both a transmitter and a receiver. The pulsed signal from the transmitter coil induces a signal in the receiver. The self-inductance of the circuit is affected by any metal object in the path (Figure 14.3.5). Metal detectors can be adjusted for sensitivity and can also sense the presence of metal on a person.

Large induced voltages are found in camera flashes. Camera flashes use a battery, two inductors that function as a transformer, and a switching system or oscillator to induce large voltages. Recall from Oscillations on oscillations that “oscillation” is defined as the fluctuation of a quantity, or repeated regular fluctuations of a quantity, between two extreme values around an average value. Also recall (from Electromagnetic Induction on electromagnetic induction) that we need a changing magnetic field, brought about by a changing current, to induce a voltage in another coil. The oscillator system does this many times as the battery voltage is boosted to over 1000 volts. (You may hear the high-pitched whine from the transformer as the capacitor is being charged.) A capacitor stores the high voltage for later use in powering the flash.
An induced emf of 2.0 V is measured across a coil of 50 closely wound turns while the current through it increases uniformly from 0.0 to 5.0 A in 0.10 s. (a) What is the self-inductance of the coil? (b) With the current at 5.0 A, what is the flux through each turn of the coil?
Strategy
Both parts of this problem give all the information needed to solve for the self-inductance in part (a) or the flux through each turn of the coil in part (b). The equations needed are Equation ??? for part (a) and Equation ??? for part (b).
Solution
- Ignoring the negative sign and using magnitudes, we have, from Equation ???, L=ϵdI/dt=2.0V5.0A/0.10s=4.0×10−2H.
- From Equation ???, the flux is given in terms of the current by Φm=LI/N, so Φm=(4.0×10−2H)(5.0A)50turns)=4.0×10−3Wb.
Significance
The self-inductance and flux calculated in parts (a) and (b) are typical values for coils found in contemporary devices. If the current is not changing over time, the flux is not changing in time, so no emf is induced.
Current flows through the inductor in Figure 14.3.4 from B to A instead of from A to B as shown. Is the current increasing or decreasing in order to produce the emf given in diagram (a)? In diagram (b)?
- Answer
-
a. decreasing; b. increasing; Since the current flows in the opposite direction of the diagram, in order to get a positive emf on the left-hand side of diagram (a), we need to decrease the current to the left, which creates a reinforced emf where the positive end is on the left-hand side. To get a positive emf on the right-hand side of diagram (b), we need to increase the current to the left, which creates a reinforced emf where the positive end is on the right-hand side.
A changing current induces an emf of 10 V across a 0.25-H inductor. What is the rate at which the current is changing?
- Answer
-
40 A/s
A good approach for calculating the self-inductance of an inductor consists of the following steps:
- Assume a current I is flowing through the inductor.
- Determine the magnetic field →B produced by the current. If there is appropriate symmetry, you may be able to do this with Ampère’s law.
- Obtain the magnetic flux, Φm.
- With the flux known, the self-inductance can be found from Equation ???, L=NΦm/I.
To demonstrate this procedure, we now calculate the self-inductances of two inductors.
Cylindrical Solenoid
Consider a long, cylindrical solenoid with length l, cross-sectional area A, and N turns of wire. We assume that the length of the solenoid is so much larger than its diameter that we can take the magnetic field to be B=μ0nI throughout the interior of the solenoid, that is, we ignore end effects in the solenoid. With a current I flowing through the coils, the magnetic field produced within the solenoid is
B=μ0(Nl)I,
so the magnetic flux through one turn is
Φm=BA=μ0NAlI.
Using Equation ???, we find for the self-inductance of the solenoid,
Lsolenoid=NΦmI=μ0N2Al.
If n=N/l is the number of turns per unit length of the solenoid, we may write Equation ??? as
L=μ0(Nl)2Al=μ0n2Al=μ0n2(V),
where V=Al is the volume of the solenoid. Notice that the self-inductance of a long solenoid depends only on its physical properties (such as the number of turns of wire per unit length and the volume), and not on the magnetic field or the current. This is true for inductors in general.
Rectangular Toroid
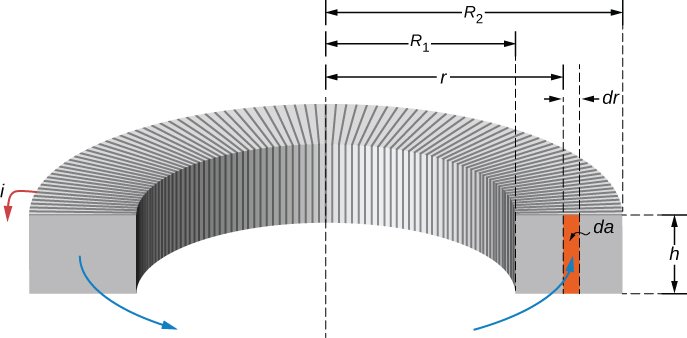
A toroid with a rectangular cross-section is shown in Figure 14.3.6. The inner and outer radii of the toroid are R1 and R2, and h is the height of the toroid. Applying Ampère’s law in the same manner as we did in Example 13.5.2 for a toroid with a circular cross-section, we find the magnetic field inside a rectangular toroid is also given by
B=μ0NI2πr,
where r is the distance from the central axis of the toroid. Because the field changes within the toroid, we must calculate the flux by integrating over the toroid’s cross-section. Using the infinitesimal cross-sectional area element da=hdr shown in Figure 14.3.6, we obtain
Φm=∫Bda=∫R2R1(μ0NI2πr)(hdr)=μ0NhI2πlnR2R1.
Now from Equation ???, we obtain for the self-inductance of a rectangular toroid
L=NΦmI=μ0N2h2πlnR2R1.
As expected, the self-inductance is a constant determined by only the physical properties of the toroid.
(a) Calculate the self-inductance of a solenoid that is tightly wound with wire of diameter 0.10 cm, has a cross-sectional area of 0.90cm2, and is 40 cm long. (b) If the current through the solenoid decreases uniformly from 10 to 0 A in 0.10 s, what is the emf induced between the ends of the solenoid?
- Answer
-
a. 4.5×10−5H; b. 4.5×10−3V
(a) What is the magnetic flux through one turn of a solenoid of self-inductance 8.0×10−5H when a current of 3.0 A flows through it? Assume that the solenoid has 1000 turns and is wound from wire of diameter 1.0 mm. (b) What is the cross-sectional area of the solenoid?
- Answer
-
a. 2.4×10−7Wb; b. 6.4×10−5m2


