14.E: Inductance (Exercise)
- Page ID
- 9555
Conceptual Questions
14.2 Mutual Inductance
1. Show that \(NΦ_m/I\) and \(ε/(dI/dt)\), which are both expressions for self-inductance, have the same units.
2. A 10-H inductor carries a current of 20 A. Describe how a 50-V emf can be induced across it.
3. The ignition circuit of an automobile is powered by a 12-V battery. How are we able to generate large voltages with this power source?
4. When the current through a large inductor is interrupted with a switch, an arc appears across the open terminals of the switch. Explain.
14.3 Self-Inductance and Inductors
5. Does self-inductance depend on the value of the magnetic flux? Does it depend on the current through the wire? Correlate your answers with the equation \(NΦ_m=LI\).
6. Would the self-inductance of a 1.0 m long, tightly wound solenoid differ from the self-inductance per meter of an infinite, but otherwise identical, solenoid?
7. Discuss how you might determine the self-inductance per unit length of a long, straight wire.
8. The self-inductance of a coil is zero if there is no current passing through the windings. True or false?
9. How does the self-inductance per unit length near the center of a solenoid (away from the ends) compare with its value near the end of the solenoid?
14.4 Energy in a Magnetic Field
10. Show that \(LI^2/2\) has units of energy.
14.5 RL Circuits
11. Use Lenz’s law to explain why the initial current in the RL circuit of Figure 14.12(b) is zero.
12. When the current in the RL circuit of Figure 14.12(b) reaches its final value \(ε/R\), what is the voltage across the inductor? Across the resistor?
13. Does the time required for the current in an RL circuit to reach any fraction of its steady-state value depend on the emf of the battery?
14. An inductor is connected across the terminals of a battery. Does the current that eventually flows through the inductor depend on the internal resistance of the battery? Does the time required for the current to reach its final value depend on this resistance?
15. At what time is the voltage across the inductor of the RL circuit of Figure 14.12(b) a maximum?
16. In the simple RL circuit of Figure 14.12(b), can the emf induced across the inductor ever be greater than the emf of the battery used to produce the current?
17. If the emf of the battery of Figure 14.12(b) is reduced by a factor of 2, by how much does the steady-state energy stored in the magnetic field of the inductor change?
18. A steady current flows through a circuit with a large inductive time constant. When a switch in the circuit is opened, a large spark occurs across the terminals of the switch. Explain.
19. Describe how the currents through \(R_1\) and \(R_2\) shown below vary with time after switch S is closed.
20. Discuss possible practical applications of RL circuits.
14.6 Oscillations in an LC Circuit
21. Do Kirchhoff’s rules apply to circuits that contain inductors and capacitors?
22. Can a circuit element have both capacitance and inductance?
23. In an LC circuit, what determines the frequency and the amplitude of the energy oscillations in either the inductor or capacitor?
14.7 RLC Series Circuits
24. When a wire is connected between the two ends of a solenoid, the resulting circuit can oscillate like an RLC circuit. Describe what causes the capacitance in this circuit.
25. Describe what effect the resistance of the connecting wires has on an oscillating LC circuit.
26. Suppose you wanted to design an LC circuit with a frequency of 0.01 Hz. What problems might you encounter?
27. A radio receiver uses an RLC circuit to pick out particular frequencies to listen to in your house or car without hearing other unwanted frequencies. How would someone design such a circuit?
Problems
14.2 Mutual Inductance
28. When the current in one coil changes at a rate of 5.6 A/s, an emf of \(6.3×10^{−3}V\). is induced in a second, nearby coil. What is the mutual inductance of the two coils?
29. An emf of \(9.7×10^{−3}V\) is induced in a coil while the current in a nearby coil is decreasing at a rate of 2.7 A/s. What is the mutual inductance of the two coils?
30. Two coils close to each other have a mutual inductance of 32 mH. If the current in one coil decays according to \(I=I_0e^{−αt}\), where \(I_0=5.0A\) and \(α=2.0×10^3s^{−1}\), what is the emf induced in the second coil immediately after the current starts to decay? At \(t=1.0×10^{−3}s\)?
31. A coil of 40 turns is wrapped around a long solenoid of cross-sectional area \(7.5×10^{−3}m^2\). The solenoid is 0.50 m long and has 500 turns.
(a) What is the mutual inductance of this system?
(b) The outer coil is replaced by a coil of 40 turns whose radius is three times that of the solenoid. What is the mutual inductance of this configuration?
32. A 600-turn solenoid is 0.55 m long and 4.2 cm in diameter. Inside the solenoid, a small (1.1cm×1.4cm), single-turn rectangular coil is fixed in place with its face perpendicular to the long axis of the solenoid. What is the mutual inductance of this system?
33. A toroidal coil has a mean radius of 16 cm and a cross-sectional area of \(0.25cm^2\); it is wound uniformly with 1000 turns. A second toroidal coil of 750 turns is wound uniformly over the first coil. Ignoring the variation of the magnetic field within a toroid, determine the mutual inductance of the two coils.
34. A solenoid of \(N_1\) turns has length \(l_1\) and radius \(R_1\), and a second smaller solenoid of \(N_2\) turns has length \(l_2\) and radius \(R_2\). The smaller solenoid is placed completely inside the larger solenoid so that their long axes coincide. What is the mutual inductance of the two solenoids?
14.3 Self-Inductance and Inductors
35. An emf of 0.40 V is induced across a coil when the current through it changes uniformly from 0.10 to 0.60 A in 0.30 s. What is the self-inductance of the coil?
36. The current shown in part (a) below is increasing, whereas that shown in part (b) is decreasing. In each case, determine which end of the inductor is at the higher potential.
37. What is the rate at which the current though a 0.30-H coil is changing if an emf of 0.12 V is induced across the coil?
38. When a camera uses a flash, a fully charged capacitor discharges through an inductor. In what time must the 0.100-A current through a 2.00-mH inductor be switched on or off to induce a 500-V emf?
39. A coil with a self-inductance of 2.0 H carries a current that varies with time according to \(I(t)=(2.0A)sin120πt\). Find an expression for the emf induced in the coil.
40. A solenoid 50 cm long is wound with 500 turns of wire. The cross-sectional area of the coil is \(2.0cm^2\) What is the self-inductance of the solenoid?
41. A coil with a self-inductance of 3.0 H carries a current that decreases at a uniform rate \(dI/dt=−0.050A/s\). What is the emf induced in the coil? Describe the polarity of the induced emf.
42. The current \(I(t)\) through a 5.0-mH inductor varies with time, as shown below. The resistance of the inductor is 5.0Ω. Calculate the voltage across the inductor at \(t=2.0ms,t=4.0ms,\) and \(t=8.0ms\).
43. A long, cylindrical solenoid with 100 turns per centimeter has a radius of 1.5 cm. (a) Neglecting end effects, what is the self-inductance per unit length of the solenoid? (b) If the current through the solenoid changes at the rate 5.0 A/s, what is the emf induced per unit length?
44. Suppose that a rectangular toroid has 2000 windings and a self-inductance of 0.040 H. If h=0.10mh=0.10m, what is the ratio of its outer radius to its inner radius?
45. What is the self-inductance per meter of a coaxial cable whose inner radius is 0.50 mm and whose outer radius is 4.00 mm?
14.4 Energy in a Magnetic Field
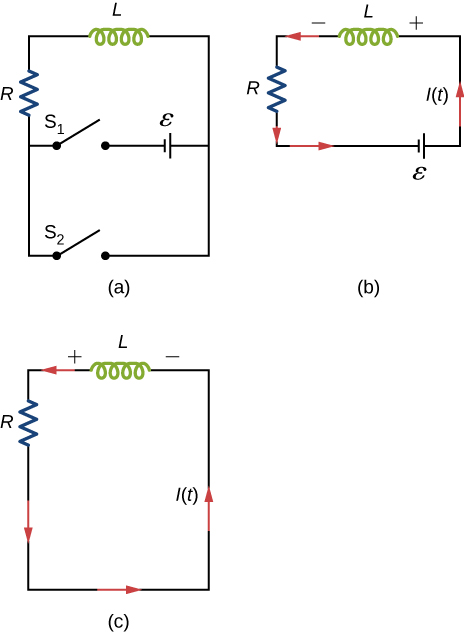
46. At the instant a current of 0.20 A is flowing through a coil of wire, the energy stored in its magnetic field is \(6.0×10^{−3}J\). What is the self-inductance of the coil?
47. Suppose that a rectangular toroid has 2000 windings and a self-inductance of 0.040 H. If \(h=0.10m\), what is the current flowing through a rectangular toroid when the energy in its magnetic field is \(2.0×10^{−6}J\)?
48. Solenoid A is tightly wound while solenoid B has windings that are evenly spaced with a gap equal to the diameter of the wire. The solenoids are otherwise identical. Determine the ratio of the energies stored per unit length of these solenoids when the same current flows through each.
49. A 10-H inductor carries a current of 20 A. How much ice at 0°C could be melted by the energy stored in the magnetic field of the inductor? (Hint: Use the value \(L_f=334J/g\) for ice.)
50. A coil with a self-inductance of 3.0 H and a resistance of 100Ω carries a steady current of 2.0 A. (a) What is the energy stored in the magnetic field of the coil? (b) What is the energy per second dissipated in the resistance of the coil?
51. A current of 1.2 A is flowing in a coaxial cable whose outer radius is five times its inner radius. What is the magnetic field energy stored in a 3.0-m length of the cable?
14.5 RL Circuits
52. In Figure 14.12, \(ε=12V, L=20mH,\) and \(R=5.0Ω\). Determine (a) the time constant of the circuit, (b) the initial current through the resistor, (c) the final current through the resistor, (d) the current through the resistor when \(t=2τ_L\), and (e) the voltages across the inductor and the resistor when \(t=2τ_L\).
53. For the circuit shown below, \(ε=20V, L=4.0mH,\) and \(R=5.0Ω\). After steady state is reached with \(S_1\) closed and \(S_2\) open, \(S_2\) is closed and immediately thereafter (at \(t=0\)) \(S_1\) is opened. Determine (a) the current through \(L\) at \(t=0\), (b) the current through \(L\) at \(t=4.0×10^{−4}s\), and (c) the voltages across \(L\) and \(R\) at \(t=4.0×10^{−4}s\). \(R_1 = R_2 = R\).
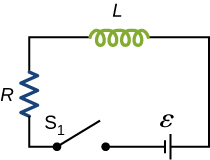
54. The current in the RL circuit shown here increases to 40% of its steady-state value in 2.0 s. What is the time constant of the circuit?
55. How long after switch \(S_1\) is thrown does it take the current in the circuit shown to reach half its maximum value? Express your answer in terms of the time constant of the circuit.
56. Examine the circuit shown below in part (a). Determine \(dI/dt\) at the instant after the switch is thrown in the circuit of
(a), thereby producing the circuit of
(b). Show that if I were to continue to increase at this initial rate, it would reach its maximum \(ε/R\) in one time constant.
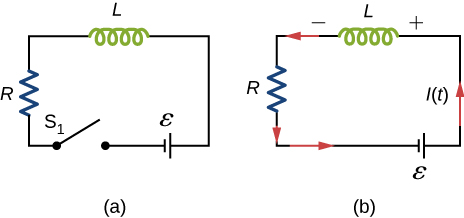
57. The current in the RL circuit shown below reaches half its maximum value in 1.75 ms after the switch \(S_1\) is thrown. Determine
(a) the time constant of the circuit and
(b) the resistance of the circuit if \(L=250mH\).
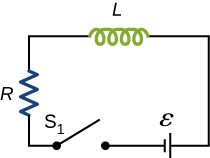
58. Consider the circuit shown below. Find \(I_1,I_2,\) and \(I_3\) when
(a) the switch S is first closed,
(b) after the currents have reached steady-state values, and
(c) at the instant the switch is reopened (after being closed for a long time).
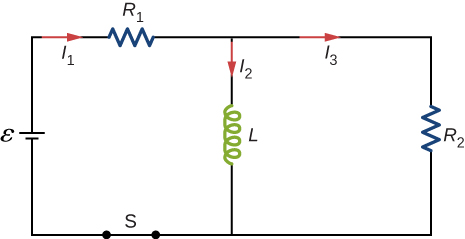
59. For the circuit shown below, \(ε=50V, R_1=10Ω, R_2=R_3=19.4Ω\) and \(L=2.0mH\). Find the values of \(I_1\) and \(I_2\)
(a) immediately after switch S is closed,
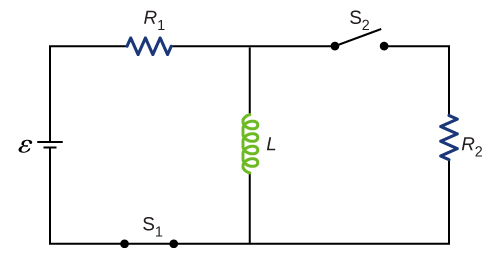
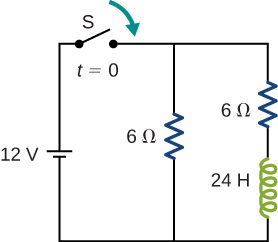
(b) a long time after S is closed,
(c) immediately after S is reopened, and
(d) a long time after S is reopened.
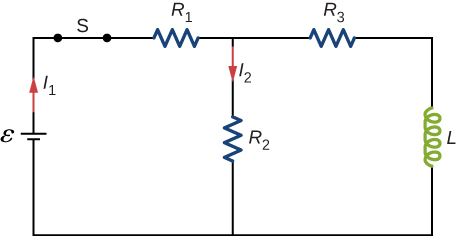
60. For the circuit shown below, find the current through the inductor \(2.0×10^{−5}s\) after the switch is reopened.
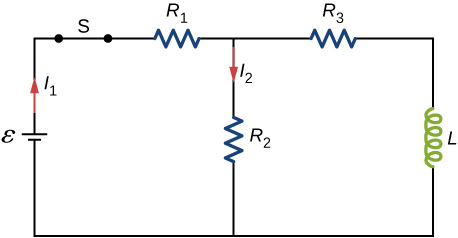
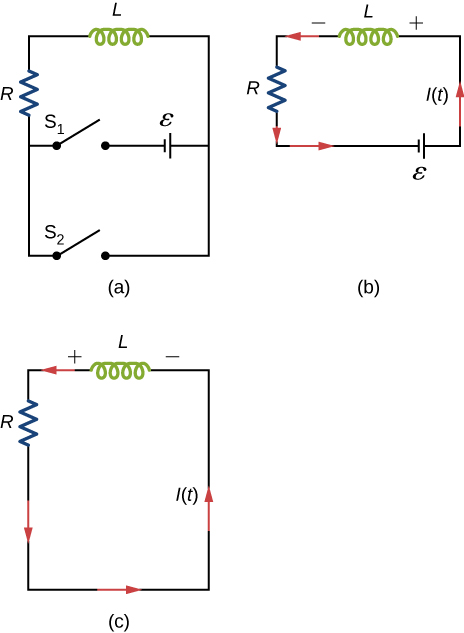
61. Show that for the circuit shown below, the initial energy stored in the inductor, \(LI^2(0)/2\), is equal to the total energy eventually dissipated in the resistor, \(∫^∞_0I^2(t)Rdt\).
14.6 Oscillations in an LC Circuit
62. A 5000-pF capacitor is charged to 100 V and then quickly connected to an 80-mH inductor. Determine
(a) the maximum energy stored in the magnetic field of the inductor,
(b) the peak value of the current, and
(c) the frequency of oscillation of the circuit.
63. The self-inductance and capacitance of an LC circuit are 0.20 mH and 5.0 pF. What is the angular frequency at which the circuit oscillates?
64. What is the self-inductance of an LC circuit that oscillates at 60 Hz when the capacitance is \(10μF\)?
65. In an oscillating LC circuit, the maximum charge on the capacitor is \(2.0×10^{−6}C\) and the maximum current through the inductor is 8.0 mA.
(a) What is the period of the oscillations?
(b) How much time elapses between an instant when the capacitor is uncharged and the next instant when it is fully charged?
66. The self-inductance and capacitance of an oscillating LC circuit are \(L=20mH\) and \(C=1.0μF\), respectively.
(a) What is the frequency of the oscillations?
(b) If the maximum potential difference between the plates of the capacitor is 50 V, what is the maximum current in the circuit?
67. In an oscillating LC circuit, the maximum charge on the capacitor is \(q_m\). Determine the charge on the capacitor and the current through the inductor when energy is shared equally between the electric and magnetic fields. Express your answer in terms of \(q_m, L,\) and \(C\).
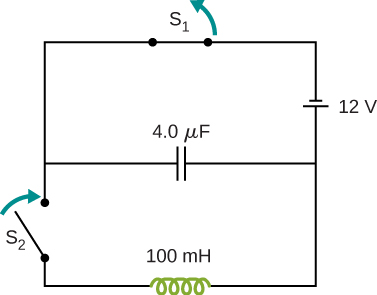
68. In the circuit shown below, \(S_1\) is opened and \(S_2\) is closed simultaneously. Determine
(a) the frequency of the resulting oscillations,
(b) the maximum charge on the capacitor,
(c) the maximum current through the inductor, and
(d) the electromagnetic energy of the oscillating circuit.
69. An LC circuit in an AM tuner (in a car stereo) uses a coil with an inductance of 2.5 mH and a variable capacitor. If the natural frequency of the circuit is to be adjustable over the range 540 to 1600 kHz (the AM broadcast band), what range of capacitance is required?
14.7 RLC Series Circuits
70. In an oscillating RLC circuit, \(R=5.0Ω,L=5.0mH\), and \(C=500μF\). What is the angular frequency of the oscillations?
71. In an oscillating RLC circuit with \(L=10mH,C=1.5µF,\) and \(R=2.0Ω\), how much time elapses before the amplitude of the oscillations drops to half its initial value?
72. What resistance R must be connected in series with a 200-mH inductor of the resulting RLC oscillating circuit is to decay to 50% of its initial value of charge in 50 cycles? To 0.10% of its initial value in 50 cycles?
Additional Problems
73. Show that the self-inductance per unit length of an infinite, straight, thin wire is infinite.
74. Two long, parallel wires carry equal currents in opposite directions. The radius of each wire is a, and the distance between the centers of the wires is d. Show that if the magnetic flux within the wires themselves can be ignored, the self-inductance of a length l of such a pair of wires is \(L=\frac{μ_0l}{π}ln\frac{d−a}{a}\). (Hint: Calculate the magnetic flux through a rectangle of length l between the wires and then use \(L=NΦ/I\).)
75. A small, rectangular single loop of wire with dimensions l, and a is placed, as shown below, in the plane of a much larger, rectangular single loop of wire. The two short sides of the larger loop are so far from the smaller loop that their magnetic fields over the smaller fields over the smaller loop can be ignored. What is the mutual inductance of the two loops?
76. Suppose that a cylindrical solenoid is wrapped around a core of iron whose magnetic susceptibility is \(x\). Using Equation 14.9, show that the self-inductance of the solenoid is given by \(L=\frac{(1+x)μ_0N^2A}{l}\), where I is its length, A its cross-sectional area, and N its total number of turns.
77. The solenoid of the preceding problem is wrapped around an iron core whose magnetic susceptibility is \(4.0×10^3\).
(a) If a current of 2.0 A flows through the solenoid, what is the magnetic field in the iron core?
(b) What is the effective surface current formed by the aligned atomic current loops in the iron core?
(c) What is the self-inductance of the filled solenoid?
78. A rectangular toroid with inner radius \(R_1=7.0cm\), outer radius \(R_2=9.0cm\), height \(h=3.0\), and \(N=3000\) turns is filled with an iron core of magnetic susceptibility \(5.2×10^3\).
(a) What is the self-inductance of the toroid?
(b) If the current through the toroid is 2.0 A, what is the magnetic field at the center of the core?
(c) For this same 2.0-A current, what is the effective surface current formed by the aligned atomic current loops in the iron core?
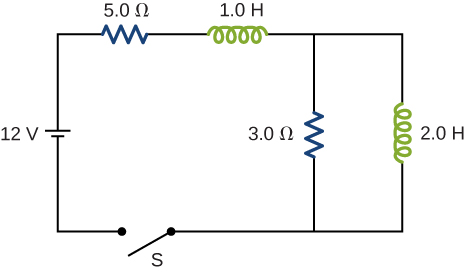
79. The switch S of the circuit shown below is closed at \(t=0\). Determine (a) the initial current through the battery and (b) the steady-state current through the battery.
80. In an oscillating RLC circuit, \(R=7.0Ω,L=10mH,\) and \(C=3.0μF\). Initially, the capacitor has a charge of \(8.0μC\) and the current is zero. Calculate the charge on the capacitor
(a) five cycles later and
(b) 50 cycles later.
81. A 25.0-H inductor has 100 A of current turned off in 1.00 ms.
(a) What voltage is induced to oppose this?
(b) What is unreasonable about this result?
(c) Which assumption or premise is responsible?
Challenge Problems
82. A coaxial cable has an inner conductor of radius a, and outer thin cylindrical shell of radius b. A current I flows in the inner conductor and returns in the outer conductor. The self-inductance of the structure will depend on how the current in the inner cylinder tends to be distributed. Investigate the following two extreme cases.
(a) Let current in the inner conductor be distributed only on the surface and find the self-inductance.
(b) Let current in the inner cylinder be distributed uniformly over its cross-section and find the self-inductance. Compare with your results in (a).
83. In a damped oscillating circuit the energy is dissipated in the resistor. The Q-factor is a measure of the persistence of the oscillator against the dissipative loss. (a) Prove that for a lightly damped circuit the energy, U, in the circuit decreases according to the following equation. \(\frac{dU}{dt}=−2βU\), where \(β=\frac{R}{2L}\). (b) Using the definition of the Q-factor as energy divided by the loss over the next cycle, prove that Q-factor of a lightly damped oscillator as defined in this problem is \(Q≡\frac{U_{begin}}{ΔU_{one \: cycle}} = \frac{1}{2 \pi R}\sqrt{\frac{L}{C}}\). (Hint: For (b), to obtain Q, divide E at the beginning of one cycle by the change \(ΔE\) over the next cycle.)
84. The switch in the circuit shown below is closed at \(t=0s\). Find currents through (a) \(R_1\), (b) \(R_2\), and (c) the battery as function of time.
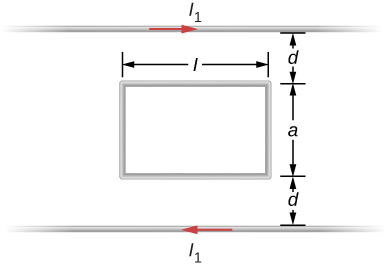
85. A square loop of side 2 cm is placed 1 cm from a long wire carrying a current that varies with time at a constant rate of 3 A/s as shown below.
(a) Use Ampère’s law and find the magnetic field as a function of time from the current in the wire.
(b) Determine the magnetic flux through the loop.
(c) If the loop has a resistance of 3Ω, how much induced current flows in the loop?
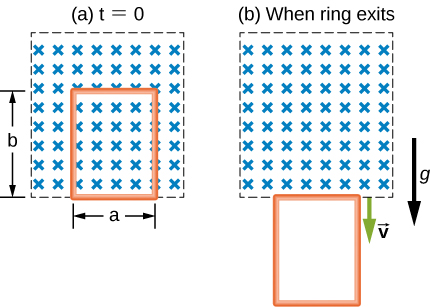
86. A rectangular copper ring, of mass 100 g and resistance 0.2Ω, is in a region of uniform magnetic field that is perpendicular to the area enclosed by the ring and horizontal to Earth’s surface. The ring is let go from rest when it is at the edge of the nonzero magnetic field region (see below).
(a) Find its speed when the ring just exits the region of uniform magnetic field.
(b) If it was let go at t=0t=0, what is the time when it exits the region of magnetic field for the following values: \(a=25cm, b=50cm,B=3T,\) and \(g=9.8m/s^2\)? Assume the magnetic field of the induced current is negligible compared to 3 T.
Contributors and Attributions
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), and Bill Moebs with many contributing authors. This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).


