7.5: Determining Field from Potential
- Page ID
- 4389
By the end of this section, you will be able to:
- Explain how to calculate the electric field in a system from the given potential
- Calculate the electric field in a given direction from a given potential
- Calculate the electric field throughout space from a given potential
Recall that we were able, in certain systems, to calculate the potential by integrating over the electric field. As you may already suspect, this means that we may calculate the electric field by taking derivatives of the potential, although going from a scalar to a vector quantity introduces some interesting wrinkles. We frequently need \(\vec{E}\) to calculate the force in a system; since it is often simpler to calculate the potential directly, there are systems in which it is useful to calculate V and then derive \(\vec{E}\) from it.
In general, regardless of whether the electric field is uniform, it points in the direction of decreasing potential, because the force on a positive charge is in the direction of \(\vec{E}\) and also in the direction of lower potential V. Furthermore, the magnitude of \(\vec{E}\) equals the rate of decrease of V with distance. The faster V decreases over distance, the greater the electric field. This gives us the following result.
In equation form, the relationship between voltage and uniform electric field is
\[E = - \dfrac{\Delta V}{\Delta s}\]
where \(\Delta s\) is the distance over which the change in potential \(\Delta V\) takes place. The minus sign tells us that \(E\) points in the direction of decreasing potential. The electric field is said to be the gradient (as in grade or slope) of the electric potential.
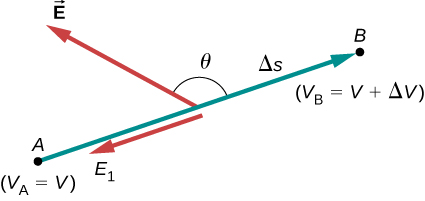
For continually changing potentials, \(\Delta V\) and \(\Delta s\) become infinitesimals, and we need differential calculus to determine the electric field. As shown in Figure \(\PageIndex{1}\), if we treat the distance \(\Delta s\) as very small so that the electric field is essentially constant over it, we find that
\[E_s = - \dfrac{dV}{ds}.\]
Therefore, the electric field components in the Cartesian directions are given by
\[E_x = - \dfrac{\partial V}{\partial x}, \, E_y = - \dfrac{\partial V}{\partial y}, \, E_z = - \dfrac{\partial V}{\partial z}.\]
This allows us to define the “grad” or “del” vector operator, which allows us to compute the gradient in one step. In Cartesian coordinates, it takes the form
\[\vec{\nabla} = \hat{i} \dfrac{\partial}{\partial x} + \hat{j} \dfrac{\partial}{\partial y} + \hat{k} \dfrac{\partial}{\partial z}.\]
With this notation, we can calculate the electric field from the potential with
\[\vec{E} = - \vec{\nabla}V, \label{eq20}\]
a process we call calculating the gradient of the potential.
If we have a system with either cylindrical or spherical symmetry, we only need to use the del operator in the appropriate coordinates:
\[\begin{align} \vec{\nabla}_{cyl} &= \underbrace{\hat{r} \dfrac{\partial}{\partial r} + \hat{\varphi}\dfrac{1}{r} \dfrac{\partial}{\partial \varphi} + \hat{z} \dfrac{\partial}{\partial z}}_{\text{Cylindrical}} \label{cylindricalnabla} \\[4pt] \vec{\nabla}_{sph} &= \underbrace{ \hat{r} \dfrac{\partial}{\partial r} + \hat{\theta}\dfrac{1}{r} \dfrac{\partial}{\partial \theta} + \hat{\varphi} \dfrac{1}{r \, sin \, \theta}\dfrac{\partial}{\partial \varphi}}_{\text{Spherical}} \label{spherenabla} \end{align}\]
Calculate the electric field of a point charge from the potential.
Strategy
The potential is known to be \(V = k\dfrac{q}{r}\), which has a spherical symmetry. Therefore, we use the spherical del operator (Equation \ref{spherenabla}) into Equation \ref{eq20}:
\[\vec{E} = - \vec{\nabla}_{sph} V \nonumber.\]
Solution
Performing this calculation gives us
\[\begin{align*} \vec{E} &= - \left( \hat{r}\dfrac{\partial}{\partial r} + \hat{\theta}\dfrac{1}{r} \dfrac{\partial}{\partial \theta} + \hat{\varphi}\dfrac{1}{1 \, \sin \, \theta} \dfrac{\partial}{\partial \varphi}\right) k\dfrac{q}{r} \\[4pt] &= - k\left( \hat{r}\dfrac{\partial}{\partial r}\dfrac{1}{r} + \hat{\theta}\dfrac{1}{r} \dfrac{\partial}{\partial \theta}\dfrac{1}{r} + \hat{\varphi}\dfrac{1}{1 \, \sin \, \theta} \dfrac{\partial}{\partial \varphi}\dfrac{1}{r}\right).\end{align*}\]
This equation simplifies to
\[\vec{E} = - kq\left(\hat{r}\dfrac{-1}{r^2} + \hat{\theta}0 + \hat{\varphi}0 \right) = k\dfrac{q}{r^2}\hat{r} \nonumber\]
as expected.
Significance
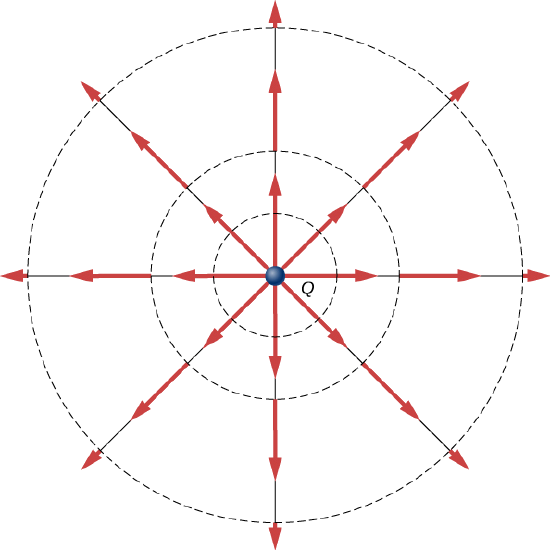
We not only obtained the equation for the electric field of a point particle that we’ve seen before, we also have a demonstration that \(\vec{E}\) points in the direction of decreasing potential, as shown in Figure \(\PageIndex{2}\).
Use the potential found previously to calculate the electric field along the axis of a ring of charge (Figure \(\PageIndex{3}\)).
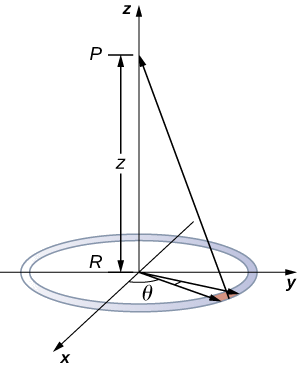
Strategy
In this case, we are only interested in one dimension, the z-axis. Therefore, we use
\[E_z = - \dfrac{\partial V}{\partial z} \nonumber\]
with the potential
\[V = k \dfrac{q_{tot}}{\sqrt{z^2 + R^2}} \nonumber\]
found previously.
Solution
Taking the derivative of the potential yields
\[ \begin{align*} E_z &= - \dfrac{\partial}{\partial z} \dfrac{kq_{tot}}{\sqrt{z^2 + R^2}} \\[4pt] &= k \dfrac{q_{tot}z}{(z^2 + R^2)^{3/2}}. \end{align*}\]
Significance
Again, this matches the equation for the electric field found previously. It also demonstrates a system in which using the full del operator is not necessary.
Which coordinate system would you use to calculate the electric field of a dipole?
- Answer
-
Any, but cylindrical is closest to the symmetry of a dipole.


