8.A: Capacitance (Answers)
- Page ID
- 10252
Check Your Understanding
8.1. \(\displaystyle 1.1×10^{−3}m\)
8.3. 3.59 cm, 17.98 cm
8.4. a. 25.0 pF;
b. 9.2
8.5. a. \(\displaystyle C=0.86pF,Q_1=10pC,Q_2=3.4pC,Q_3=6.8pC\);
b. \(\displaystyle C=2.3pF,Q_1=12pC,Q_2=Q_3=16pC\);
c. \(\displaystyle C=2.3pF,Q_1=9.0pC,Q_2=18pC,Q_3=12pC,Q_4=15pC\)
8.6. a.\(\displaystyle 4.0×10^{−13}J\); b. 9 times
8.7. a. 3.0; b. \(\displaystyle C=3.0C_0\)
8.9. a. \(\displaystyle C_0=20pF, C=42pF\);
b. \(\displaystyle Q_0=0.8nC, Q=1.7nC\);
c. \(\displaystyle V_0=V=40V\); d. \(\displaystyle U_0=16nJ, U=34nJ\)
Conceptual Questions
1. no; yes
3. false
5. no
7. \(\displaystyle 3.0μF,0.33μF\)
9. answers may vary
11. Dielectric strength is a critical value of an electrical field above which an insulator starts to conduct; a dielectric constant is the ratio of the electrical field in vacuum to the net electrical field in a material.
13. Water is a good solvent.
15. When energy of thermal motion is large (high temperature), an electrical field must be large too in order to keep electric dipoles aligned with it.
17. answers may vary
Problems
19. 21.6 mC
21. 1.55 V
23. 25.0 nF
25. \(\displaystyle 1.1×10^{−3}m^2\)
27. 500 µC
29. 1:16
31. a. 1.07 nC;
b. 267 V, 133 V
33. \(\displaystyle 0.29μF\)
34. 500 capacitors; connected in parallel
35. \(\displaystyle 3.08μF\) (series) and \(\displaystyle 13.0μ\) (parallel)
37. \(\displaystyle 11.4μF\)
39. 0.89 mC; 1.78 mC; 444 V
41. \(\displaystyle 7.5μJ\)
43. a. 405 J; b. 90.0 mC
45. 1.15 J
47. a. \(\displaystyle 4.43×10^{−9}F\);
b. 0.453 V;
c. \(\displaystyle 4.53×10^{−10}J\);
d. no
49. 0.7 mJ
51. a. 7.1 pF;
b. 42 pF
53. a. before 3.00 V; after 0.600 V;
b. before 1500 V/m; after 300 V/m
55. a. 3.91;
b. 22.8 V
57. a. 37 nC;
b. 0.4 MV/m;
c. 19 nC
59. a. \(\displaystyle 4.4μF\);
b. \(\displaystyle 4.0×10^{-5}C\)
61. \(\displaystyle 0.0135m^2\)
63. \(\displaystyle 0.185μJ\)
Additional Problems
65. a. 0.277 nF;
b. 27.7 nC;
c. 50 kV/m
67. a. 0.065 F;
b. 23,000 C;
c. 4.0 GJ
69. a. \(\displaystyle 75.6μC\); b. 10.8 V
71. a. 0.13 J;
b. no, because of resistive heating in connecting wires that is always present, but the circuit schematic does not indicate resistors
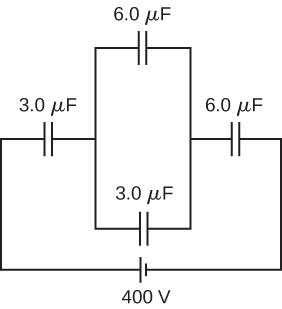
73. a. \(\displaystyle −3.00μF\);
b. You cannot have a negative \(\displaystyle C_2\) capacitance.
c. The assumption that they were hooked up in parallel, rather than in series, is incorrect. A parallel connection always produces a greater capacitance, while here a smaller capacitance was assumed. This could only happen if the capacitors are connected in series.
75. a. 14.2 kV;
b. The voltage is unreasonably large, more than 100 times the breakdown voltage of nylon.
c. The assumed charge is unreasonably large and cannot be stored in a capacitor of these dimensions.
Challenge Problems
77. a. 89.6 pF;
b. 6.09 kV/m;
c. 4.47 kV/m;
d. no
79. a. 421 J;
b. 53.9 mF
81. \(\displaystyle C=ε_0A/(d_1+d_2)\)
83. proof
Contributors and Attributions
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), and Bill Moebs with many contributing authors. This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).


