2.3: Scalars and Vectors (Part 2)
- Page ID
- 3972
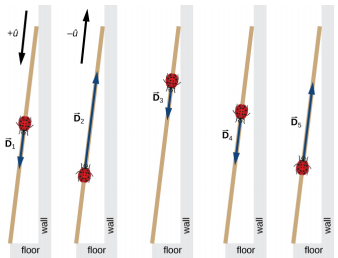
A long measuring stick rests against a wall in a physics laboratory with its 200-cm end at the floor. A ladybug lands on the 100-cm mark and crawls randomly along the stick. It first walks 15 cm toward the floor, then it walks 56 cm toward the wall, then it walks 3 cm toward the floor again. Then, after a brief stop, it continues for 25 cm toward the floor and then, again, it crawls up 19 cm toward the wall before coming to a complete rest (Figure \(\PageIndex{1}\)). Find the vector of its total displacement and its final resting position on the stick.
Strategy
If we choose the direction along the stick toward the floor as the direction of unit vector \(\hat{u}\), then the direction toward the floor is \(+ \hat{u}\) and the direction toward the wall is \(−\hat{u}\). The ladybug makes a total of five displacements:
\[ \begin{align*} \vec{D}_{1} &= (15\; cm)( + \hat{u}), \\[4pt] \vec{D}_{2} &= (56\; cm)( - \hat{u}), \\[4pt] \vec{D}_{3} &= (3\; cm)( + \hat{u}), \\[4pt] \vec{D}_{4} &= (25\; cm)( + \hat{u}), \; and \\[4pt] \vec{D}_{5} &= (19\; cm)( - \hat{u}) \ldotp \end{align*}\]
The total displacement \(\vec{D}\) is the resultant of all its displacement vectors.
Solution
The resultant of all the displacement vectors is
\[ \begin{align*} \vec{D} &= \vec{D}_{1} + \vec{D}_{2} + \vec{D}_{3} + \vec{D}_{4} + \vec{D}_{5} \\[4pt] &= (15\; cm)( + \hat{u} ) + (56\; cm)( −\hat{u} ) + (3\; cm)( + \hat{u} ) + (25\; cm)( + \hat{u}) + (19\; cm)( − \hat{u}) \\[4pt] &= (15 − 56 + 3 + 25 − 19) cm\; \hat{u} \\[4pt] &= −32\; cm\; \hat{u} \ldotp \end{align*}\]
In this calculation, we use the distributive law given by Equation 2.2.9. The result reads that the total displacement vector points away from the 100-cm mark (initial landing site) toward the end of the meter stick that touches the wall. The end that touches the wall is marked 0 cm, so the final position of the ladybug is at the (100 – 32) cm = 68-cm mark.
A cave diver enters a long underwater tunnel. When her displacement with respect to the entry point is 20 m, she accidentally drops her camera, but she doesn’t notice it missing until she is some 6 m farther into the tunnel. She swims back 10 m but cannot find the camera, so she decides to end the dive. How far from the entry point is she? Taking the positive direction out of the tunnel, what is her displacement vector relative to the entry point?
Algebra of Vectors in Two Dimensions
When vectors lie in a plane—that is, when they are in two dimensions—they can be multiplied by scalars, added to other vectors, or subtracted from other vectors in accordance with the general laws expressed by Equation 2.2.1, Equation 2..2.2, Equation 2.2.7, and Equation 2.2.8. However, the addition rule for two vectors in a plane becomes more complicated than the rule for vector addition in one dimension. We have to use the laws of geometry to construct resultant vectors, followed by trigonometry to find vector magnitudes and directions. This geometric approach is commonly used in navigation (Figure \(\PageIndex{2}\)). In this section, we need to have at hand two rulers, a triangle, a protractor, a pencil, and an eraser for drawing vectors to scale by geometric constructions.
For a geometric construction of the sum of two vectors in a plane, we follow the parallelogram rule. Suppose two vectors \(\vec{A}\) and \(\vec{B}\) are at the arbitrary positions shown in Figure \(\PageIndex{3}\). Translate either one of them in parallel to the beginning of the other vector, so that after the translation, both vectors have their origins at the same point. Now, at the end of vector \(\vec{A}\) we draw a line parallel to vector \(\vec{B}\) and at the end of vector \(\vec{B}\) we draw a line parallel to vector \(\vec{A}\) (the dashed lines in Figure \(\PageIndex{3}\)). In this way, we obtain a parallelogram. From the origin of the two vectors we draw a diagonal that is the resultant \(\vec{R}\) of the two vectors: \(\vec{R}\) = \(\vec{A}\) + \(\vec{B}\) (Figure \(\PageIndex{3a}\)). The other diagonal of this parallelogram is the vector difference of the two vectors \(\vec{D}\) = \(\vec{A}\) − \(\vec{B}\), as shown in Figure \(\PageIndex{3b}\). Notice that the end of the difference vector is placed at the end of vector \(\vec{A}\).
It follows from the parallelogram rule that neither the magnitude of the resultant vector nor the magnitude of the difference vector can be expressed as a simple sum or difference of magnitudes A and B, because the length of a diagonal cannot be expressed as a simple sum of side lengths. When using a geometric construction to find magnitudes |\(\vec{R}\)| and |\(\vec{D}\)|, we have to use trigonometry laws for triangles, which may lead to complicated algebra. There are two ways to circumvent this algebraic complexity. One way is to use the method of components, which we examine in the next section. The other way is to draw the vectors to scale, as is done in navigation, and read approximate vector lengths and angles (directions) from the graphs. In this section we examine the second approach.
If we need to add three or more vectors, we repeat the parallelogram rule for the pairs of vectors until we find the resultant of all of the resultants. For three vectors, for example, we first find the resultant of vector 1 and vector 2, and then we find the resultant of this resultant and vector 3. The order in which we select the pairs of vectors does not matter because the operation of vector addition is commutative and associative (see Equation 2.2.7 and Equation 2.2.8). Before we state a general rule that follows from repetitive applications of the parallelogram rule, let’s look at the following example.
Suppose you plan a vacation trip in Florida. Departing from Tallahassee, the state capital, you plan to visit your uncle Joe in Jacksonville, see your cousin Vinny in Daytona Beach, stop for a little fun in Orlando, see a circus performance in Tampa, and visit the University of Florida in Gainesville. Your route may be represented by five displacement vectors \(\vec{A}\), \(\vec{B}\), \(\vec{C}\), \(\vec{D}\), and \(\vec{E}\), which are indicated by the red vectors in Figure \(\PageIndex{4}\). What is your total displacement when you reach Gainesville? The total displacement is the vector sum of all five displacement vectors, which may be found by using the parallelogram rule four times. Alternatively, recall that the displacement vector has its beginning at the initial position (Tallahassee) and its end at the final position (Gainesville), so the total displacement vector can be drawn directly as an arrow connecting Tallahassee with Gainesville (see the green vector in Figure \(\PageIndex{4}\)). When we use the parallelogram rule four times, the resultant \(\vec{R}\) we obtain is exactly this green vector connecting Tallahassee with Gainesville: \(\vec{R}\) = \(\vec{A}\) + \(\vec{B}\) + \(\vec{C}\) + \(\vec{D}\) + \(\vec{E}\).
Drawing the resultant vector of many vectors can be generalized by using the following tail-to-head geometric construction. Suppose we want to draw the resultant vector \(\vec{R}\) of four vectors \(\vec{A}\), \(\vec{B}\), \(\vec{C}\), and \(\vec{D}\) (Figure \(\PageIndex{5a}\)). We select any one of the vectors as the first vector and make a parallel translation of a second vector to a position where the origin (“tail”) of the second vector coincides with the end (“head”) of the first vector. Then, we select a third vector and make a parallel translation of the third vector to a position where the origin of the third vector coincides with the end of the second vector. We repeat this procedure until all the vectors are in a head-to-tail arrangement like the one shown in Figure \(\PageIndex{5}\). We draw the resultant vector \(\vec{R}\) by connecting the origin (“tail”) of the first vector with the end (“head”) of the last vector. The end of the resultant vector is at the end of the last vector. Because the addition of vectors is associative and commutative, we obtain the same resultant vector regardless of which vector we choose to be first, second, third, or fourth in this construction.
The three displacement vectors \(\vec{A}\), \(\vec{B}\), and \(\vec{C}\) in Figure \(\PageIndex{6}\) are specified by their magnitudes A = 10.0, B = 7.0, and C = 8.0, respectively, and by their respective direction angles with the horizontal direction \(\alpha\) = 35°, \(\beta\) = −110°, and \(\gamma\) = 30°. The physical units of the magnitudes are centimeters. Choose a convenient scale and use a ruler and a protractor to find the following vector sums: (a) \(\vec{R}\) = \(\vec{A}\) + \(\vec{B}\), (b) \(\vec{D}\) = \(\vec{A}\) − \(\vec{B}\), and (c) \(\vec{S}\) = \(\vec{A}\) − \(3 \vec{B}\) + \(\vec{C}\).
Strategy
In geometric construction, to find a vector means to find its magnitude and its direction angle with the horizontal direction. The strategy is to draw to scale the vectors that appear on the right-hand side of the equation and construct the resultant vector. Then, use a ruler and a protractor to read the magnitude of the resultant and the direction angle. For parts (a) and (b) we use the parallelogram rule. For (c) we use the tail-to-head method.
Solution
For parts (a) and (b), we attach the origin of vector \(\vec{B}\) to the origin of vector \(\vec{A}\), as shown in Figure \(\PageIndex{7}\), and construct a parallelogram. The shorter diagonal of this parallelogram is the sum \(\vec{A}\) + \(\vec{B}\). The longer of the diagonals is the difference \(\vec{A}\) − \(\vec{B}\). We use a ruler to measure the lengths of the diagonals, and a protractor to measure the angles with the horizontal. For the resultant \(\vec{R}\), we obtain R = 5.8 cm and \(\theta_{R}\) ≈ 0°. For the difference \(\vec{D}\), we obtain D = 16.2 cm and \(\theta_{D}\) = 49.3°, which are shown in Figure \(\PageIndex{7}\).
For (c), we can start with vector −3 \(\vec{B}\) and draw the remaining vectors tail-to-head as shown in Figure \(\PageIndex{8}\). In vector addition, the order in which we draw the vectors is unimportant, but drawing the vectors to scale is very important. Next, we draw vector \(\vec{S}\) from the origin of the first vector to the end of the last vector and place the arrowhead at the end of \(\vec{S}\). We use a ruler to measure the length of \(\vec{S}\), and find that its magnitude is S = 36.9 cm. We use a protractor and find that its direction angle is \(\theta_{S}\) = 52.9°. This solution is shown in Figure \(\PageIndex{8}\).
Using the three displacement vectors \(\vec{A}\), \(\vec{B}\), and \(\vec{F}\) in Figure \(\PageIndex{6}\), choose a convenient scale, and use a ruler and a protractor to find vector \(\vec{G}\) given by the vector equation \(\vec{G}\) = \(\vec{A}\) + \(2 \vec{B}\) − \(\vec{F}\).
Observe the addition of vectors in a plane by visiting this vector calculator and this PhET simulation.


