7.3: The "Center of Mass Work"

Last updated
Save as PDF

Page ID: 22241

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

All the physics I used in order to derive the result (7.2.8) was \(F = ma\), and the expression \(v^2_f −v^2_i = 2a\Delta x\), which applies whenever we have motion with constant acceleration. Now, we know that for an arbitrary system, of total mass \(M\), \(F_{ext,net} = M a_{cm}\) [see Equation (6.1.11)]. That is enough, then, to ensure that, if \(F_{ext,net}\) is a constant, we will have

\[ F_{\text {ext,net}} \Delta x_{c m}=\Delta K_{c m} \label{eq:7.12} \]

where \(K_{cm}\), the translational kinetic energy, is, as usual, \(K_{cm} = \frac{1}{2}Mv^2_{cm}\), and \(\Delta x_{cm}\) is the displacement of the center of mass. The result (\ref{eq:7.12}) holds for an arbitrary system, as long as \(F_{ext,net}\) is constant, and can be generalized by means of an integral (as in Equation (7.2.6)) when it is variable.

So it seems that we could define the left-hand side of Equation (\ref{eq:7.12}) as “the work done on the center of mass,” and take that as the natural generalization to a system of the result (7.2.8) for a particle. Most physicists would, in fact, be OK with that, but educators nowadays frown on that idea, for a couple of reasons.

First, it seems that it is essential to the notion of work that one should multiply the force by the displacement of the object on which it is acting. More precisely, in the definition (7.2.1), we want the displacement of the point of application of the force¹. But there are many examples of systems where there is nothing at the precise location of the center of mass, and certainly no force acting precisely there.

This is not necessarily a problem in the case of a rigid object which is not doing anything funny, just moving as a whole so that every part has the same displacement, because then the displacement of the center of mass would simply stand for the displacement of any point at which an external force might actually be applied. But for many deformable systems, this would not be case. In fact, for such systems one can usually show that \(F_{ext,net} \Delta x_{cm} \) is actually not the work done on the system by the net external force. A simple example of such a system is shown below, in Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\): A system of two blocks connected by a spring. A constant external force, \(\vec F^c_{h,2}\), is applied to the block on the right. Initially the spring is relaxed, but as soon as block 2 starts to move it stretches, pulling back on block 2 and pulling forward on block 1. Because of the stretching of the spring, the displacements \(\Delta x_1\), \(\Delta x_{cm}\) and \(\Delta x_2\) are all different, and the work done by the external force, \(F^c_{h,2} \Delta x_2\), is different from the “center of mass work” \(F^c_{h,2} \Delta x_{cm}\).

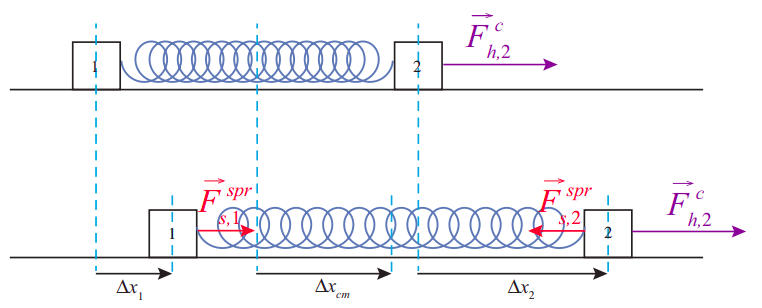
In this figure, the two blocks are connected by a spring, and the external force is applied to the block on the right (block 2). If the blocks have the same mass, the center of mass of the system is a point exactly halfway between them. If the spring starts in its relaxed state, it will stretch at first, so that the center of mass will lag behind block 2, and \(F^c_{h,2} \Delta x_2\), which is the quantity that we should properly call the “work done by the net external force” will not be equal to \(F^c_{h,2} \Delta x_{cm}\).

We find ourselves, therefore, with a very general and potentially rather useful result, Equation (\ref{eq:7.12}), that looks a lot like it should be “the work done on the system by the net external force” but, in fact, is that only sometimes. On the other hand, the result is so useful that simply referring to it all the time by “Equation (\ref{eq:7.12})” will not do. I propose, therefore, to call it the “center of mass work,” in between quotation marks, just so we all know what we are talking about, and remember the caveats that go with it.

We can now move to the real theorem relating the work of the external forces on a system to the change in its energy. What we have seen so far are really just straightforward applications of Newton’s second law. The main result coming up is deeper than that, since it involves also, ultimately, the principle of conservation of energy.

¹As the name implies, this is the precise point at which the force is applied. For contact forces (other than friction; see later), this is easily identified. For gravity, a sum over all the forces exerted on all the particles that make up the object may be shown to be equivalent to a single resultant force acting at a point called the center of gravity, which, for our purposes (objects in uniform or near-uniform gravitational fields) will be the same as the center of mass.