8.3: Inclined Planes
- Page ID
- 22248
Back in Chapter 2, I stated without proof that the acceleration of an object sliding, without friction, down an inclined plane making an angle \(\theta\) with the horizontal was \(g \sin \theta\). I can show you now why this is so, and introduce friction as well.
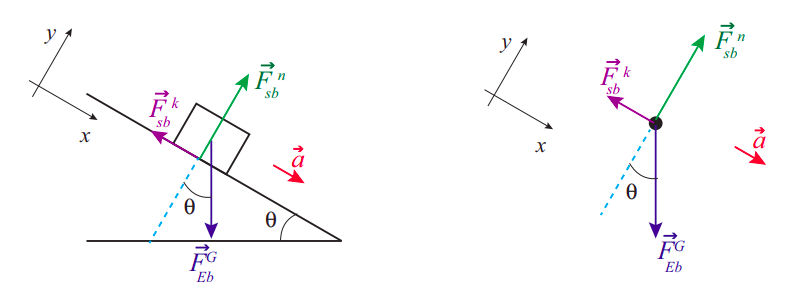
Figure \(\PageIndex{1}\) above shows, on the left, a block sliding down an inclined plane and all the forces acting on it. These are more clearly seen on the free-body diagram on the right. I have labeled all the forces using the \(\vec{F}_{b y, o n}^{t y p e}\) convention introduced back in Chapter 6 (so, for instance, \(\vec{F}_{sb}^{k}\) is the force of kinetic friction exerted by the surface on the block); however, later on, for algebraic manipulations, and especially where \(x\) and \(y\) components need to be taken, I will drop the “by, on” subscripts, and just let the “type” superscript identify the force in question.
The diagrams also show the coordinate axes I have chosen: the \(x\) axis is along the plane, and the \(y\) is perpendicular to it. The advantage of this choice is obvious: the motion is entirely along one of the axes, and two of the forces (the normal force and the friction) already lie along the axes. The only force that does not is the block’s weight (that is, the force of gravity), so we need to decompose it into its \(x\) and \(y\) components. For this, we can make use of the fact, which follows from basic geometry, that the angle of the incline, \(\theta\), is also the angle between the vector \(\vec F^g\) and the negative \(y\) axis. This means we have
\begin{align}
&F_{x}^{g}=F^{g} \sin \theta \nonumber \\
&F_{y}^{g}=-F^{g} \cos \theta \label{eq:8.14}.
\end{align}
Equations (\ref{eq:8.14}) also show another convention I will adopt from now, namely, that whenever the symbol for a vector is shown without an arrow on top or an \(x\) or \(y\) subscript, it will be understood to refer to the magnitude of the vector, which is always a positive number by definition.
Newton’s second law, as given by equations (8.2.1) applied to this system, then reads:
\[ F_{x}^{g}+F_{x}^{k}=m a_{x}=F^{g} \sin \theta-F^{k} \label{eq:8.15} \]
for the motion along the plane, and
\[ F_{y}^{g}+F_{y}^{n}=m a_{y}=-F^{g} \cos \theta+F^{n} \label{eq:8.16} \]
for the direction perpendicular to the plane. Of course, since there is no motion in this direction, \(a_y\) is zero. This gives us immediately the value of the normal force:
\[ F^{n}=F^{g} \cos \theta=m g \cos \theta \label{eq:8.17} \]
since \(F^g = mg\). We can also use the result (\ref{eq:8.17}), together with Equation (6.3.9), to get the magnitude of the friction force, assuming we know the coefficient of kinetic (or sliding) friction, \(\mu_k\):
\[ F^{k}=\mu_{k} F^{n}=\mu_{k} m g \cos \theta \label{eq:8.18} .\]
Substituting this and \(F^G = mg\) in Equation (\ref{eq:8.15}), we get
\[ m a_{x}=m g \sin \theta-\mu_{k} m g \cos \theta \label{eq:8.19} .\]
We can eliminate the mass to obtain finally
\[ a_{x}=g\left(\sin \theta-\mu_{k} \cos \theta\right) \label{eq:8.20} \]
which is the desired result. In the absence of friction (\(\mu_k\) = 0) this gives \(a = g \sin \theta\), as we had in Chapter 2. Note that, if you reduce the tilt of the surface (that is, make \(\theta\) smaller), the \(\cos \theta\) term in Equation (\ref{eq:8.20}) grows and the \(\sin \theta\) term gets smaller, so we must make sure that we do not use this equation when \(\theta\) is too small or we would get the absurd result that \(a_x\) < 0, that is, that the force of kinetic friction has overcome gravity and is accelerating the object upwards!
Of course, we know from experience that what happens when \(\theta\) is very small is that the block does not slide: it is held in place by the force of static friction. The diagram for such a situation looks the same as Figure \(\PageIndex{1}\), except that \(\vec a\) = 0, the force of friction is \(F^s\) instead of \(F^k\), and of course its magnitude must match that of the \(x\) component of gravity. Equation (\ref{eq:8.15}) then becomes
\[ m a_{x}=0=F^{g} \sin \theta-F^{s} \label{eq:8.21} .\]
Recall from Chapter 6 that the force of static friction does not have a fixed value: rather, it will match the applied force up to a maximum value given by Equation (6.3.8):
\[ F_{\max }^{s}=\mu_{s} F^{n}=\mu_{s} m g \cos \theta \label{eq:8.22} \]
where I have used Equation (\ref{eq:8.17}), since clearly the equation (\ref{eq:8.16}) still applies along the vertical direction. So, on the one hand we have the requirement that \(F^s = mg \sin \theta\) to keep the block from sliding, and on the other hand the constraint \(F^{s} \leq \mu_{s} m g \cos \theta\). Putting these together we conclude that the block will not slide as long as
\[ m g \sin \theta \leq \mu_{s} m g \cos \theta \label{eq:8.23} \]
or
\[ \tan \theta \leq \mu_{s} \label{eq:8.24} .\]
In short, as long as \(\theta\) is small enough to satisfy Equation (\ref{eq:8.24}), the block will not move. Once \(\theta\) exceeds the value \(\tan ^{-1} \mu_{s}\), we can apply the result (\ref{eq:8.20}\)) for the acceleration. Note that, since we always have \(\mu_{s} \geq \mu_{k}\), the result (\ref{eq:8.20}) will always be positive if \(\theta>\tan ^{-1} \mu_{s}\), that is, if \(\sin \theta>\mu_{s} \cos \theta\).
What if we send the block sliding up the plane instead? The acceleration would still be pointing down (since the object would be slowing down all the while), but now the force of kinetic friction would point in the direction opposite that indicated in Figure \(\PageIndex{1}\), since it always must oppose the motion. If you go through the same analysis I carried out above, you will get that \(a_x = g (\sin \theta + \mu_k \cos \theta)\) in that case, since now friction and gravity are working together to slow the motion down.


