2.1.2: Period, Frequency, Amplitude, Restoring Force, Phase
- Page ID
- 26138
A motion that repeats itself over time is said to be periodic and has a period, \(T\), measured in seconds. Simple harmonic motion is an example of periodic motion. The period is defined to be the time it takes for the vibrating object to make one cycle or oscillation and return to its original position. The inverse of period is called the frequency, \(f\) where \(f=1/T\). Frequency is measured in hertz (\(\text{Hz}\)) which is a cycle or oscillation per second. So if a vibration repeats every \(0.004\text{ s}\) it has a period of \(0.004\text{ s}\) and a frequency of \(1/0.004\text{ s} = 250\text{ Hz}\). A \(500\text{ Hz}\) frequency means that whatever is vibrating oscillates with a period of \(1/500\text{ Hz} = 0.002\text{ s}\).
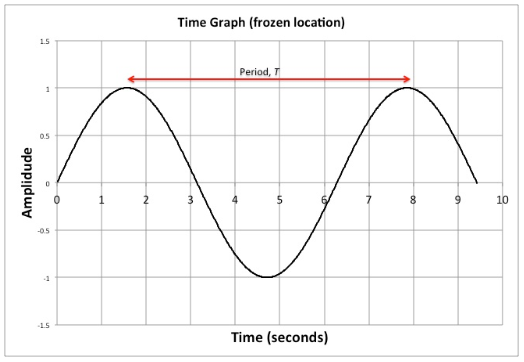
Figure \(\PageIndex{1}\)
When a guitar string or clarinet reed is at rest it is in its equilibrium position. When it is vibrating its displacement (Chapter 2), measured in meters or centimeters, is constantly changing. At some point in time a point on the string or reed reaches a maximum displacement and then moves in the opposite direction until it reaches a maximum in the other direction before turning around again. This maximum displacement from equilibrium at a given point is called the amplitude. You may hear the word 'amplitude' used to mean 'displacement' at times other than the maximum but strictly speaking this isn't correct. Amplitude can also describe the maximum of other quantities which vary periodically. For example the speed of a vibrating reed also changes periodically and so has a speed amplitude which is the maximum speed.
Not only does the displacement change over time (from a maximum in one direction to a maximum in the other) but the velocity of the vibrating object is continually changing. As the object reaches its maximum displacement it slows down, stops and turns around (think of a mass attached to the end of a spring). We know from Chapter 1 that a change in velocity is an acceleration and accelerations are caused by forces. So to vibrate, an object has to have a force acting on it. This force always acts to push the object back towards its equilibrium position. This is called a restoring force.
The Phase tells where we are in a cycle when we start making a time measurement of the motion. Phase is measured as an angle in degrees or radians (\(2π\text{ radians} = 360\text{ degrees}\)). Imagine a pendulum swinging back and forth and we want to measure its period. We could start our stopwatch when the pendulum is all the way to the right and then stop it when the pendulum returns to its original position. Or we could start when the pendulum is all the way to the left and wait for it to return all the way to the left. Or we could start the stopwatch exactly when the pendulum is straight up and down, moving to the right and stop the measurement when the pendulum is again straight up and down, moving to the right again (it would be straight up and down once in between but moving to the left; the motion hasn't fully repeated so this isn't a full period). In all three cases we would get the same number of seconds for the period, \(T\). The difference is where the pendulum was in its motion when we started our stopwatch. By convention we start with the pendulum straight up and down and moving to the right which is given a phase of zero (degrees or radians). Once it has gone through an entire cycle it has traveled \(360\text{ degrees}\) or \(2π\text{ radians}\).
If the pendulum is all the way to the right it is \(1/4\) of the way through the period from when we started compared to the straight up and down case. So it has an initial phase of \(1/4\) of \(360\) or \(90\text{ degrees} = π/2\text{ radians}\) of a cycle. With the pendulum all the way to the left it is \(3/4\) of the way through the cycle or \(270\text{ degrees} = 3π/4\text{ radians}\) when it starts. We can take data for the period starting at any time (not just at a maximum amplitude) and still accurately describe the motion by including the phase (sometimes called the phase angle) in our description. As we will see, many interesting sound phenomena occur when two sound waves arrive at a microphone or your ear which are not in phase with each other.
Note
Both simple harmonic motion and many waves can be described by the trigonometric functions sine and cosine. What is the difference between these two functions? A sine function starts with an amplitude of zero (\(\sin (0)=0\)) whereas a cosine function starts with an amplitude of one (\(\cos (0)=1\)). If we slide the sine function to the left by \(90\text{ degrees} = π/2\text{ radians}\) it exactly matches a cosine curve. In other words the sine and cosine are out of phase by \(90\text{ degrees}\); \(\sin (x+\pi /2)=\cos (x)\) for any \(x\). So we can use either function by adjusting the phase appropriately.
Video/audio examples:
- Examples of oscillation (some are simple harmonic, others not).
- Simple harmonic motion: explanation and examples.
- Tuning fork in water in slow motion.
- Brass player's lips vibrating.
- Example of a nonlinear spring. Note that the frequency shifts upward over time, unlike a linear system where the frequency remains constant when the amplitude changes.


