2: The distance to asteroid 2002 NY40 via parallax
- Page ID
- 3604
During the middle of August, 2002, asteroid 2002 NY40 zoomed close past the Earth, coming within about 1.5 lunar orbital radii. Lee Smallwood of the US Naval Academy and I decided to measure the parallax of the asteroid, since it would be large enough to yield a reasonably precise distance. But when? The asteroid would move so fast during its closest approach that it would leave long trails on even the shortest exposures. On the other hand, the closer it was, the brighter. There was a clear trade-off.
In the end, the weather took the decision out of our hands. Storms were forecast for both Rochester and Annapolis over the weekend of August 17-18. We watched the satellite images closely and called each other for regular updates. On the night of August 16/17 EDT, holes appeared in the cloud banks above both sites, and we got to work.
Our plan was to take 10-second exposures at regular intervals, always starting at the top of a minute (that is, starting at exactly 12:10:00 or 12:16:00). We started with 5-minute intervals at midnight EDT, then switched to 2-minute intervals from 12:20 to 01:00 AM. I had some problems with the filter wheel on our camera, and some problems thinking straight at that hour, so I didn't manage to get an image at every desired interval. Still, I managed enough that we should have at least 5 or 6 simultaneous pairs.
The asteroid was moving very quickly. Below are two images taken at RIT, using out 10-inch Meade LX-200 with f/6.3 focal reducer, SBIG ST-8E CCD camera and V-band filter. Each image has North up, East to the left, and covers an area roughly 24 arcminutes wide by 17 arcminutes tall.
Start time: 12:06:41 EDT.

Start time: 12:07:41 EDT.


Rochester vs. Annapolis
Below is an image taken at RIT; the midpoint of the 10-second exposure was UT 2002 Aug 17 04:22:06. The field is centered near RA = 20:57:20, Dec = +04:47:15. Note that the asteroid is moving so fast that it leaves a bit of a trail even in this short exposure. If you click on the image, you'll enter a page where you can blink this image and a simultaneous image taken in Annapolis.

If you do a little geometry, you can turn this parallax into the distance between the Earth and the asteroid at this time. You need to know:
- location of RIT Observatory: lat 43.0758 North, long 77.6647 West
- location of USNA Observatory: lat 38.9838 North, long 76.4847 West
- the plate scale, which you can determine by looking at this chart and noting that the stars marked "A" and "B" are 269 arcseconds apart
Exercise \(\PageIndex{2}\)
- How far from the Earth was 2002 NY40 at the time of these pictures?
- Using the pair of images taken 5 minutes apart, calculate the speed (km/s) of the asteroid relative to the Earth.
- Estimate the speed of the asteroid relative to the Sun.
Limits of two-observatory parallax
This technique of observing an object simultaneously from two different places on Earth works fine for finding the parallax of objects which aren't too far from Earth: the Moon, Venus, Mars, asteroids which zip past the Earth. But how well does it work for more distant objects?
Assume that the two observatories are located on opposite sides of the Earth, and assume further that they can make accurate measurements when looking "sideways", at objects just above their local horizons. Calculate the parallax angle, in arcseconds, for
- Mars at opposition
- Jupiter at opposition
- Neptune at opposition
- the second-nearest star, Proxima Centauri, located very roughly 4 light years away from the Sun
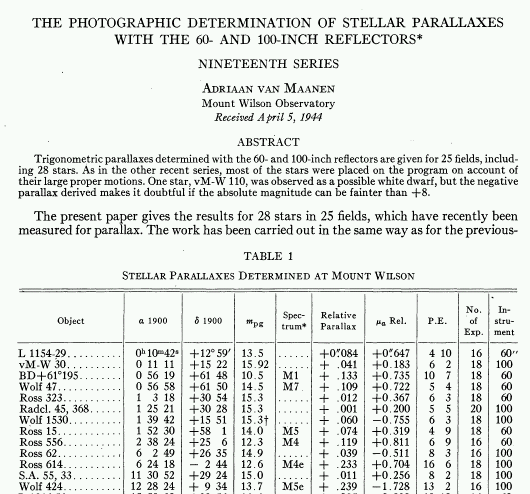
Just how precisely can astronomers measure the tiny shifts in angular position caused by parallax? Consider this set of measurements made by Adriaan van Maanen in the 1940s, using the Mt. Wilson 60-inch and 100-inch telescopes. (You can read the entire article by looking it up in the ADS system )
A more recent parallax survey was made by the Hipparcos satellite. Here's a brief summary of its results:

How do these observational precisions compare to the precision necessary to resolve stellar parallax from two locations on the ground?


