5.3: Wavefunction of Spin One-Half Particle
- Page ID
- 1206
The state of a spin one-half particle is represented as a vector in ket space. Let us suppose that this space is spanned by the basis kets \( \vert x', y', z', \pm\rangle\) denotes a simultaneous eigenstate of the position operators \( y\), \( S_z\), corresponding to the eigenvalues \( y'\), \( \pm \hbar/2\), respectively. The basis kets are assumed to satisfy the completeness relation
where the \( L_z\) ) acting on the product 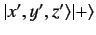 by assuming that it operates only on the \( \vert+\rangle\) factor. Similarly, we can give a meaning to any spin operator (such as \( S_z\) ) acting on
by assuming that it operates only on the \( \vert+\rangle\) factor. Similarly, we can give a meaning to any spin operator (such as \( S_z\) ) acting on 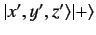 by assuming that it operates only on \( \vert x', y', z'\rangle\). This implies that every position space operator commutes with every spin operator. In this manner, we can give meaning to the equation
by assuming that it operates only on \( \vert x', y', z'\rangle\). This implies that every position space operator commutes with every spin operator. In this manner, we can give meaning to the equation
A general state \( A\) of a spin one-half particle is represented as a ket \( \psi_+(x', y', z')\)
Contributors
Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)
\( \newcommand {\ltapp} {\stackrel {_{\normalsize<}}{_{\normalsize \sim}}}\) \(\newcommand {\gtapp} {\stackrel {_{\normalsize>}}{_{\normalsize \sim}}}\) \(\newcommand {\btau}{\mbox{\boldmath$\tau$}}\) \(\newcommand {\bmu}{\mbox{\boldmath$\mu$}}\) \(\newcommand {\bsigma}{\mbox{\boldmath$\sigma$}}\) \(\newcommand {\bOmega}{\mbox{\boldmath$\Omega$}}\) \(\newcommand {\bomega}{\mbox{\boldmath$\omega$}}\) \(\newcommand {\bepsilon}{\mbox{\boldmath$\epsilon$}}\)


