In the absence of spin, the Hamiltonian can be written as some function of the position and momentum operators. Using the Schrödinger representation, in which \({\bf p} \rightarrow -{\rm i}\,\hbar\,\nabla\), the energy eigenvalue problem,
\[H\,\vert E\rangle = E\,\vert E\rangle, \label{520}\]
can be transformed into a partial differential equation for the wavefunction \( {\bf x}'\) . In general, we find
| \( H\) is now a partial differential operator. The boundary conditions (for a bound state) are obtained from the normalization constraint |
| \( \psi_+({\bf x'})\), specifies the probability density of observing the particle at position \( {\bf x}'\) with spin angular momentum \( z\) -direction. The second, \( {\bf x}'\) with spin angular momentum \( z\) -direction. In the Pauli scheme, these wavefunctions are combined into a spinor, \( \psi_+\) and \( H \,\chi = E \,\chi,\) | \ref{523} |
where \( 2\times 1\) matrix of wavefunctions) and \( H\) is a \( \psi_+\) and \( 2\times 2\) matrix partial differential operator in the Schrödinger/Pauli scheme [see Equation \ref{506}]. In other words, the partial differential equation for \( \psi_-\) . In fact, both equations have the same form, so there is only really one differential equation. In this situation, the most general solution to Equation \ref{523} can be written
| \( \psi({\bf x}')\) is determined by the solution of the differential equation, and the \( 2\times 2\) matrix of complex numbers in the Schrödinger/Pauli scheme [see Equation \ref{489}], and the spinor eigenvalue equation \ref{523} reduces to a straightforward matrix eigenvalue problem. The most general solution can again be written |
\( c_+/c_-\) is determined by the matrix eigenvalue problem, and the wavefunction \( \psi_+\) and \( s\) particle: i.e., a particle for which the eigenvalue of \( s\,(s+1)\,\hbar^2\) . Here, \( S_z\) are written \( s_z\) is allowed to take the values \( 2\,s+1\) distinct allowed values of \( 2\,s+1\) different wavefunctions, denoted 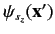 . Here, . Here, 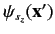 specifies the probability density for observing the particle at position \( {\bf x'}\) with spin angular momentum \( z\) -direction. More exactly, specifies the probability density for observing the particle at position \( {\bf x'}\) with spin angular momentum \( z\) -direction. More exactly, |
\( \vert\vert A\rangle\rangle\) denotes a state ket in the product space of the position and spin operators. The state of the particle can be represented more succinctly by a spinor, \( 2\,s+1\) component column vector of the 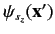 . Thus, a spin one-half particle is represented by a two-component spinor, a spin one particle by a three-component spinor, a spin three-halves particle by a four-component spinor, and so on. . Thus, a spin one-half particle is represented by a two-component spinor, a spin one particle by a three-component spinor, a spin three-halves particle by a four-component spinor, and so on. In this extended Schrödinger/Pauli scheme, position space operators take the form of diagonal \( p_k \rightarrow -{\rm i}\,\hbar \,\frac{\partial}{\partial x_k'}\, {\bf 1},\) | \ref{527} |
where \( {\bf 1}\) is the \( S_k \rightarrow s\,\hbar \,\sigma_k,\)
\ref{528} | where the \( \sigma_k\) has elements
| \( j, l\) are integers, or half-integers, lying in the range \( +s\) . But, how can we evaluate the brackets \( \sigma_z\) matrix. By definition, |
| \( (\sigma_3)_{j\,l} = \frac{\langle s, j\vert\,S_z\, \vert s, l\rangle}{s\,\hbar} = \frac{j}{s}\, \delta_{j\,l},\) | \ref{531} |
where use has been made of the orthonormality property of the \( \sigma_z\) is the suitably normalized diagonal matrix of the eigenvalues of \( \sigma_x\) and \( S^\pm = S_x \pm {\rm i}\, S_y.\)
\ref{532} | We know, from Equations \ref{344}-\ref{345}, that
| \( = [s\,(s+1) - j \,(j+1)]^{1/2} \,\hbar\, \vert s, j+1\rangle,\) | \ref{533} |
| \( = [s\,(s+1) - j \,(j-1)]^{1/2}\, \hbar \,\vert s, j-1\rangle.\) | \ref{534} |
It follows from Equations \ref{529}, and \ref{532}-\ref{534}, that
| \( = \frac{[s\,(s+1) - j\,(j-1)]^{1/2} }{2\,s}\,\delta_{j\,\, l+1}+ \frac{[s\,(s+1) - j\,(j+1)]^{1/2} }{2\,s}\,\delta_{j\,\, l-1},\) | \ref{535} |
| \( = \frac{[ s\,(s+1) - j\,(j-1)]^{1/2} }{2\,{\rm i}\,s}\,\delta_{j\,\, l+1}- \frac{[s\,(s+1) - j\,(j+1)]^{1/2} }{2\,{\rm i}\,s}\,\delta_{j\,\, l-1}.\) | \ref{536} |
According to Equations \ref{531} and \ref{535}-\ref{536}, the Pauli matrices for a spin one-half (\( \sigma_1\)
\( \sigma_2\) | \( \sigma_3\) | \( s=1\) ) particle, we find that | | \( =\frac{1}{\sqrt{2}}\left(\! \begin{array}{rrr} 0 &1&0\\ 1&0&1\\ 0&1&0\end{array}\!\right),\) | \ref{540} |
| \( = \frac{1}{\sqrt{2}} \left(\!\begin{array}{rrr} 0 &-{\rm i}&0\\ {\rm i}&0&{-\rm i}\\ 0&{\rm i}& 0\end{array}\!\right),\) | \ref{541} |
| \( = \left(\!\begin{array}{rrr} 1 &0&0\\ 0&0&0\\ 0&0&-1\end{array}\!\right).\) | \ref{542} |
In fact, we can now construct the Pauli matrices for a spin anything particle. This means that we can convert the general energy eigenvalue problem for a spin-\( 2\,s+1\) coupled partial differential equations involving the \( \psi_{s_z}({\bf x'})\) . Unfortunately, such a system of equations is generally too complicated to solve exactly.
Contributors
Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)
\( \newcommand {\ltapp} {\stackrel {_{\normalsize<}}{_{\normalsize \sim}}}\) \(\newcommand {\gtapp} {\stackrel {_{\normalsize>}}{_{\normalsize \sim}}}\) \(\newcommand {\btau}{\mbox{\boldmath$\tau$}}\) \(\newcommand {\bmu}{\mbox{\boldmath$\mu$}}\) \(\newcommand {\bsigma}{\mbox{\boldmath$\sigma$}}\) \(\newcommand {\bOmega}{\mbox{\boldmath$\Omega$}}\) \(\newcommand {\bomega}{\mbox{\boldmath$\omega$}}\) \(\newcommand {\bepsilon}{\mbox{\boldmath$\epsilon$}}\)


