7.8: Zeeman Effect

Last updated
Save as PDF

Page ID: 1223

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Consider a hydrogen-like atom placed in a uniform $z$-directed magnetic field. The change in energy of the outermost electron is

\[H_B = - {\bf \mu} \cdot {\bf B}, \label{710}\]

where

$ \mbox{\boldmath$$ = - \frac{e}{2\,m_e}\, ({\bf L} + 2 \,{\bf S})$ \ref{711}

is its magnetic moment, including both the spin and orbital contributions. Thus,

$ H_B = \frac{e\, B}{2\, m_e}\, (L_z + 2\, S_z).$ \ref{712}

Suppose that the energy-shifts induced by the magnetic field are much smaller than those induced by spin-orbit interaction. In this situation, we can treat $ H_B$ as a small perturbation acting on the eigenstates of $ H_0 + H_{LS}$ . Of course, these states are the simultaneous eigenstates of $ J^{\,2}$ and $ J_z$ . Let us consider one of these states, labeled by the quantum numbers $ j$ and $ m$ , where $ j=l\pm 1/2$ . From standard perturbation theory, the first-order energy-shift in the presence of a magnetic field is

$ {\mit\Delta} E_{nlm\pm} = \langle l\pm 1/2, m\vert\, H_B\, \vert l\pm 1/2, m\rangle.$ \ref{713}

Because

$ L_z + 2 \,S_z = J_z + S_z,$ \ref{714}

we find that

$ {\mit\Delta} E_{nlm\pm} = \frac{e\, B}{2 \,m_e}\, \left(m\,\hbar + \langle l\pm 1/2, m\vert\, S_z\,\vert l\pm 1/2, m\rangle\, \right).$ \ref{715}

Now, from Equations \ref{695}-\ref{696},

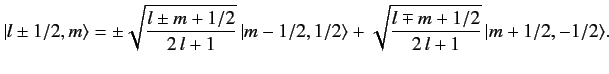
$\vert l\pm 1/2, m\rangle = \pm \sqrt{\frac{l\pm m +1/2}{2\,l+1}}\... ... m-1/2, 1/2\rangle+\sqrt{\frac{l\mp m+1/2}{2\,l+1}}\, \vert m+1/2, -1/2\rangle.$ \ref{716}

It follows that

$\langle l\pm 1/2, m\vert\, S_z\,\vert l\pm 1/2, m\rangle = \frac{... ...+1)} \left[(l\pm m+1/2) - (l\mp m + 1/2) \right] = \pm \frac{m\,\hbar}{2\,l+1}.$ \ref{717}

Thus, we obtain the so-called Lande formula for the energy-shift induced by a weak magnetic field:

$ {\mit\Delta} E_{nlm\pm} = \frac{e\, \hbar\, B}{2\, m_e}\,m \left( 1 \pm \frac{1}{2\,l+1} \right).$ \ref{718}

Let us apply this theory to the sodium atom. We have already seen that the non-Coulomb potential splits the degeneracy of the $ 3s$ and $ 3p$ states, the latter states acquiring a higher energy. The spin-orbit interaction splits the six $ 3p$ states into two groups, with four $ j=3/2$ states lying at a slightly higher energy than two $ j=1/2$ states. According to Equation \ref{718}, a magnetic field splits the $ (3p)_{3/2}$ quadruplet of states, each state acquiring a different energy. In fact, the energy of each state becomes dependent on the quantum number $ m$ , which measures the projection of the total angular momentum along the $ z$ -axis. States with higher $ m$ values have higher energies. A magnetic field also splits the $ (3p)_{1/2}$ doublet of states. However, it is evident from Equation \ref{718} that these states are split by a lesser amount than the $ j=3/2$ states.

Suppose that we increase the strength of the magnetic field, so that the energy-shift due to the magnetic field becomes comparable to the energy-shift induced by spin-orbit interaction. Clearly, in this situation, it does not make much sense to think of $ H_B$ as a small interaction term operating on the eigenstates of $ H_0 + H_{LS}$ . In fact, this intermediate case is very difficult to analyze. Let us, instead, consider the extreme limit in which the energy-shift due to the magnetic field greatly exceeds that induced by spin-orbit effects. This is called the Paschen-Back limit.

In the Paschen-Back limit, we can think of the spin-orbit Hamiltonian, $ H_{LS}$ , as a small interaction term operating on the eigenstates of $ H_0 + H_B$ . Note that the magnetic Hamiltonian, $ H_B$ , commutes with $ L^2, S^{\,2}, L_z, S_z$ , but does not commute with $L^2, S^{\,2}, J^{\,2}, J_z$ . Thus, in an intense magnetic field, the energy eigenstates of a hydrogen-like atom are approximate eigenstates of the spin and orbital angular momenta, but are not eigenstates of the total angular momentum. We can label each state by the quantum numbers $ n$ (the energy quantum number), $ l$ , $ m_l$ , and $ m_s$ . Thus, our energy eigenkets are written $ \vert n, l,m_l, m_s\rangle$ . The unperturbed Hamiltonian, $ H_0$ , causes states with different values of the quantum numbers $ n$ and $ l$ to have different energies. However, states with the same value of $ n$ and $ l$ , but different values of $ m_l$ and $ m_s$ , are degenerate. The shift in energy due to the magnetic field is simply

$ {\mit\Delta} E_{n\,l\,m_l\, m_s}= \langle n,l,m_l, m_s\vert\, H_B\,\vert n,l,m_l, m_s\rangle = \frac{e\, \hbar \,B} {2 \,m_e} \,(m_l + 2 \,m_s).$ \ref{719}

Thus, states with different values of $ m_l + 2\, m_s$ acquire different energies.

Let us apply this result to a sodium atom. In the absence of a magnetic field, the six $ 3p$ states form two groups of four and two states, depending on the values of their total angular momentum. In the presence of an intense magnetic field, the $ 3p$ states are split into five groups. There is a state with $ m_l+2\,m_s = 2$ , a state with $ m_l+2\,m_s = 1$ , two states with $ m_l+2\,m_s = 0$ , a state with $ m_l+2\,m_s = -1$ , and a state with $ m_l+2\,m_s = -2$ . These groups are equally spaced in energy, the energy difference between adjacent groups being $ e \,\hbar\, B/ 2\,m_e$ .

The energy-shift induced by the spin-orbit Hamiltonian is given by

$ {\mit\Delta} E_{n\,l\,m_l \,m_s} = \langle n,l,m_l, m_s\vert\,H_{LS}\,\vert n,l,m_l, m_s\rangle,$ \ref{720}

where

$ H_{LS} = \frac{1}{2 \,m_e^{\,2}\,c^2} \frac{1}{r} \frac{dV}{dr} \,{\bf L}\cdot {\bf S}.$ \ref{721}

Now,

$ \langle {\bf L}\cdot {\bf S}\rangle = \langle\, L_z \,S_z + (L^+\, S^- + L^- \,S^+)/2\, \rangle= \hbar^2\, m_l\, m_s,$ \ref{722}

since

$ \langle L^\pm \rangle = \langle S^\pm\rangle = 0$ \ref{723}

for expectation values taken between the simultaneous eigenkets of $ L_z$ and $ S_z$ . Thus,

$ {\mit\Delta} E_{n\,l\, m_l\, m_s} = \frac{\hbar^2\, m_l \,m_s} {2 \,m_e^{\,2}\,c^2} \left\langle \frac{1}{r} \frac{d V}{dr}\right\rangle.$ \ref{724}

Let us apply the above result to a sodium atom. In the presence of an intense magnetic field, the $ 3p$ states are split into five groups with ($ m_l,m_s$ ) quantum numbers $ (1,1/2)$ , $ (0,1/2)$ , $ (1,-1/2)$ or $ (-1, 1/2)$ , $ (0,-1/2)$ , and $ (-1,-1/2)$ , respectively, in order of decreasing energy. The spin-orbit term increases the energy of the highest energy state, does not affect the next highest energy state, decreases, but does not split, the energy of the doublet, does not affect the next lowest energy state, and increases the energy of the lowest energy state. The net result is that the five groups of states are no longer equally spaced in energy.

The typical magnetic field-strength needed to access the Paschen-Bach limit is

$ B_{PB} \sim \alpha^2 \frac{e\, m_e}{\epsilon_0\, h \,a_0} \simeq 25\,\,\,{\rm tesla}.$ \ref{725}

Contributors

Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)

$ \newcommand {\ltapp} {\stackrel {_{\normalsize<}}{_{\normalsize \sim}}}$ $\newcommand {\gtapp} {\stackrel {_{\normalsize>}}{_{\normalsize \sim}}}$ $\newcommand {\btau}{\mbox{\boldmath$\tau$}}$ $\newcommand {\bmu}{\mbox{\boldmath$\mu$}}$ $\newcommand {\bsigma}{\mbox{\boldmath$\sigma$}}$ $\newcommand {\bOmega}{\mbox{\boldmath$\Omega$}}$ $\newcommand {\bomega}{\mbox{\boldmath$\omega$}}$ $\newcommand {\bepsilon}{\mbox{\boldmath$\epsilon$}}$