7.P: Exercises
- Page ID
- 1225
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
- Calculate the energy-shift in the ground state of the one-dimensional harmonic oscillator when the perturbation
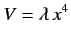 is added to
is added to 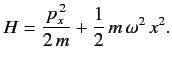 The properly normalized ground-state wavefunction is
The properly normalized ground-state wavefunction is 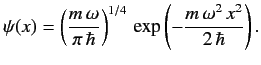
- Calculate the energy-shifts due to the first-order Stark effect in the \( n=3\) state of a hydrogen atom. You do not need to perform all of the integrals, but you should construct the correct linear combinations of states.
- The Hamiltonian of the valence electron in a hydrogen-like atom can be written
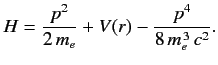 Here, the final term on the right-hand side is the first-order correction due to the electron's relativistic mass increase. Treating this term as a small perturbation, deduce that it causes an energy-shift in the energy eigenstate characterized by the standard quantum numbers \( n\) , \( l\) , \( m\) of
Here, the final term on the right-hand side is the first-order correction due to the electron's relativistic mass increase. Treating this term as a small perturbation, deduce that it causes an energy-shift in the energy eigenstate characterized by the standard quantum numbers \( n\) , \( l\) , \( m\) of 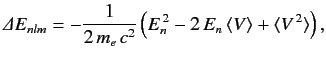 where \( E_n\) is the unperturbed energy, and \( \alpha\) the fine structure constant.
where \( E_n\) is the unperturbed energy, and \( \alpha\) the fine structure constant. - Consider an energy eigenstate of the hydrogen atom characterized by the standard quantum numbers \( n\) , \( l\) , and \( m\) . Show that if the energy-shift due to spin-orbit coupling (see Section 7.7) is added to that due to the electron's relativistic mass increase (see previous exercise) then the net fine structure energy-shift can be written
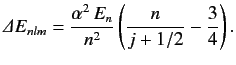 Here, \( E_n\) is the unperturbed energy, \( \alpha\) the fine structure constant, and \( j=l\pm 1/2\) the quantum number associated with the magnitude of the sum of the electron's orbital and spin angular momenta. You will need to use the following standard results for a hydrogen atom:
Here, \( E_n\) is the unperturbed energy, \( \alpha\) the fine structure constant, and \( j=l\pm 1/2\) the quantum number associated with the magnitude of the sum of the electron's orbital and spin angular momenta. You will need to use the following standard results for a hydrogen atom:
Contributors
Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)
\( \newcommand {\ltapp} {\stackrel {_{\normalsize<}}{_{\normalsize \sim}}}\) \(\newcommand {\gtapp} {\stackrel {_{\normalsize>}}{_{\normalsize \sim}}}\) \(\newcommand {\btau}{\mbox{\boldmath$\tau$}}\) \(\newcommand {\bmu}{\mbox{\boldmath$\mu$}}\) \(\newcommand {\bsigma}{\mbox{\boldmath$\sigma$}}\) \(\newcommand {\bOmega}{\mbox{\boldmath$\Omega$}}\) \(\newcommand {\bomega}{\mbox{\boldmath$\omega$}}\) \(\newcommand {\bepsilon}{\mbox{\boldmath$\epsilon$}}\)


