8.2: General Analysis

Suppose that at $\vert A\rangle = \sum_n c_n\, \vert n\rangle,$ $\ref{741}$

where the $\vert A, t_0, t\rangle = \sum_n c_n \exp[-{\rm i}\,E_n \,(t-t_0)/\hbar]\,\vert n\rangle.$ $\ref{742}$

Now, the probability of finding the system in state $t$ is

$H_1= 0$ , the probability of finding the system in state $t$ is exactly the same as the probability of finding the system in this state at the initial time $H_1\neq 0$ , we expect $\vert A, t_0, t\rangle = \sum_n c_n(t) \exp[-{\rm i}\,E_n\,(t-t_0)/\hbar]\,\vert n\rangle,$ $\ref{744}$

where $c_n(t)$ , which depends entirely on the perturbation (i.e., $H_1= 0$ ). Note that the eigenkets $H_0$ evaluated at the time ${\rm i}\,\hbar\, \frac{\partial}{\partial t}\,\vert A, t_0, t\rangle = H\,\vert A,t_0,t\rangle= (H_0+H_1) \,\vert A,t_0,t\rangle.$ $\ref{745}$

It follows from Equation $\ref{744}$ that

$(H_0+H_1)\, \vert A,t_0,t\rangle = \sum_m c_m(t) \exp[-{\rm i}\,E_m\, (t-t_0)/\hbar]\, (E_m + H_1)\,\vert m\rangle.$ $\ref{746}$

We also have

$\ref{747}$

where use has been made of the time-independence of the kets $\vert m\rangle$ . According to Equation $\ref{745}$, we can equate the right-hand sides of the previous two equations to obtain

$\ref{748}$

Left-multiplication by ${\rm i}\,\hbar\, \frac{d c_n}{dt} = \sum_m H_{nm}(t)\, \exp[\,{\rm i}\,\omega_{nm}\, (t-t_0)]\, c_m(t),$ $\ref{749}$

where

$\omega_{nm} = \frac{E_n - E_m}{\hbar}.$ $\ref{751}$

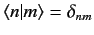Here, we have made use of the standard orthonormality result, . Suppose that there are $c_n$ , which specify the probability of finding the system in state $t$ , is determined by $N=2$ ), it is actually possible to solve Equation $\ref{749}$ without approximation. This solution is of great practical importance.

Contributors

• Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)

  $\newcommand {\ltapp} {\stackrel {_{\normalsize<}}{_{\normalsize \sim}}}$ $\newcommand {\gtapp} {\stackrel {_{\normalsize>}}{_{\normalsize \sim}}}$ $\newcommand {\btau}{\mbox{\boldmath$\tau$}}$ $\newcommand {\bmu}{\mbox{\boldmath$\mu$}}$ $\newcommand {\bsigma}{\mbox{\boldmath$\sigma$}}$ $\newcommand {\bOmega}{\mbox{\boldmath$\Omega$}}$ $\newcommand {\bomega}{\mbox{\boldmath$\omega$}}$ $\newcommand {\bepsilon}{\mbox{\boldmath$\epsilon$}}$