9.2: Fundamental
- Page ID
- 1239
Consider time-independent scattering theory, for which the Hamiltonian of the system is written
and \( \vert\phi\rangle\) be an energy eigenket of \( H_0\, \vert\phi\rangle = E\, \vert\phi\rangle,\) whose wavefunction \( \phi({\bf x}')\) . This state is assumed to be a plane wave state or, possibly, a spherical wave state. Schrödinger's equation for the scattering problem is where where Thus, Equation \ref{916} becomes Let us suppose that the scattering Hamiltonian, \( \langle {\bf x}'\vert\,H_1\,\vert{\bf x}\rangle = V({\bf x})\, \delta({\bf x} -{\bf x}').\) We can write Thus, the integral equation \ref{919} simplifies to Suppose that the initial state \( {\bf k}\) (i.e., a stream of particles of definite momentum \( \vert{\bf k}\rangle\) . The associated wavefunction takes the form The wavefunction is normalized such that Suppose that the scattering potential \( {\bf x} = {\bf0}\) ). Let us calculate the wavefunction \( r\gg r'\) . It is easily demonstrated that Clearly, \( {\bf k}'\) is the wavevector for particles that possess the same energy as the incoming particles (i.e., \( \exp(\pm {\rm i}\, k\,\vert{\bf x} - {\bf x}' \vert\,) \simeq \exp(\pm {\rm i}\, k \,r) \exp(\mp {\rm i}\, {\bf k}' \cdot {\bf x}').\) In the large-\( r\) limit, Equation \ref{922} reduces to The first term on the right-hand side is the incident wave. The second term represents a spherical wave centred on the scattering region. The plus sign (on \( \psi({\bf x}) = \frac{1}{(2\pi)^{3/2}} \left[\exp(\,{\rm i}\,{\bf k}\cdot{\bf x}) + \frac{\exp(\,{\rm i}\,k\,r)}{r} f({\bf k}', {\bf k}) \right],\) where Let us define the differential cross-section, \( d{\mit\Omega}\) , divided by the incident flux of particles. Recall, from Chapter 3, that the probability current (i.e., the particle flux) associated with a wavefunction \( {\bf j} = \frac{\hbar}{m}\, {\rm Im}(\psi^\ast\, \nabla \psi).\) Thus, the probability flux associated with the incident wavefunction, Likewise, the probability flux associated with the scattered wavefunction, Now, Thus, \( \hbar\,{ \bf k}\) to be scattered into states whose momentum vectors are directed in a range of solid angles \( \hbar\,{ \bf k}'\) . Note that the scattered particles possess the same energy as the incoming particles (i.e., \( k'=k\) ). This is always the case for scattering Hamiltonians of the form specified in Equation \ref{920}. Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)\ref{912} is an energy eigenstate of the total Hamiltonian whose wavefunction \( \psi({\bf x}')\) . In general, both \( H_0+H_1\) have continuous energy spectra: i.e., their energy eigenstates are unbound. We require a solution of Equation \ref{913} that satisfies the boundary condition \( H_1\rightarrow 0\) . Here, \( (\nabla^2 + k^2)\,\psi({\bf x}) = \frac{2\,m}{\hbar^2}\, \langle {\bf x} \vert\,H_1\,\vert \psi\rangle,\) \( \vert\psi\rangle\) \ref{914} \( \psi({\bf x}) = \phi({\bf x}) + \frac{2\,m}{\hbar^2} \int d^3 x'\,G({\bf x}, {\bf x}') \,\langle {\bf x}' \vert\,H_1\,\vert\psi\rangle,\) \ref{916} as \( G({\bf x}, {\bf x}') = -\frac{\exp(\pm {\rm i}\,k\, \vert{\bf x} - {\bf x}'\vert\,)}{4\pi\,\vert{\bf x} - {\bf x}'\vert}.\) \( \vert\psi\rangle \rightarrow \vert\phi\rangle\) \ref{918} 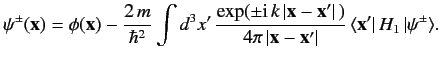
\ref{919} \ref{920} 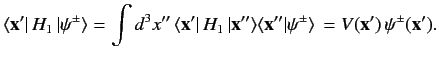
\ref{921} 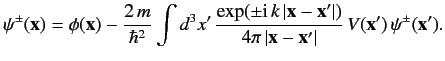
\ref{922} \( \langle {\bf x} \vert {\bf k}\rangle = \frac{ \exp(\,{\rm i}\,{\bf k}\cdot{\bf x}) }{(2\pi)^{3/2}}.\) \ref{923} ![$ \langle {\bf k}\vert{\bf k}'\rangle =\int d^3 x\, \langle {\bf k}...
...\, {\bf x}\cdot({\bf k} -{\bf k}')]} {(2\pi )^3} = \delta ({\bf k} - {\bf k'}).$](http://farside.ph.utexas.edu/teaching/qm/lectures/img2159.png)
\ref{924} , where\( r'/r\) and \( {\bf k}' = k\,{\bf e}_r.\) \( r=\vert{\bf x}\vert\) \ref{927} \ref{928} 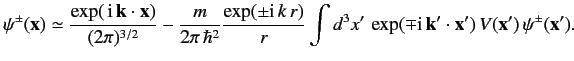
\ref{929} \ref{930} 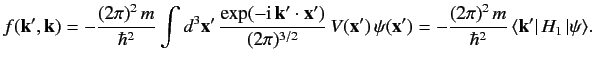
\ref{931} \ref{932} \( {\bf j}_{\rm inc} = \frac{\hbar}{(2\pi)^{3}\,m} \,{\bf k}.\) \ref{934} \( {\bf j}_{\rm sca}=\frac{\hbar}{(2\pi)^{3}\,m} \frac{\vert f( {\bf k}', {\bf k})\vert^{\,2}}{r^2} \, k\, {\bf e}_r.\) \ref{936} \( \frac{d\sigma}{d {\mit\Omega}} = \vert f({\bf k}', {\bf k})\vert^{\,2}.\) \ref{938} Contributors


