11.3: Lorentz Invariance of Dirac Equation
- Page ID
- 1255
Consider two inertial frames, \( S'\) . Let the \( x^{\,\mu'}\) be the space-time coordinates of a given event in each frame, respectively. These coordinates are related via a Lorentz transformation, which takes the general form
Now, since [see Equation \ref{1102}]
Moreover, it is easily shown that
By definition, a 4-vector \( x^{\,\mu}\) . Thus,
etc.
In frame \( \left[\gamma^{\,\mu}\left(p_\mu- \frac{e}{c}\,{\mit\Phi}_\mu\right)-m_e\,c\right]\psi = 0.\) Let \( S'\) . Suppose that\ref{1153} is a \( x^{\,\mu}\) . (Hence, \( A\) commutes with the \( {\mit\Phi}_\mu\) .) Multiplying \ref{1153} by \( A\) , we obtain\( A\)
Suppose that
Here, we have assumed that the \( A\) and the \( \left[\gamma^{\,\mu}\left(p_{\mu'}- \frac{e}{c}\,{\mit\Phi}_{\mu'}\right)-m_e\,c\right]\psi' = 0.\) A comparison of this equation with \ref{1153} reveals that the Dirac equation takes the same form in frames \( S'\) . In other words, the Dirac equation is Lorentz invariant. Incidentally, it is clear from \ref{1153} and \ref{1159} that the \( A\) that satisfies \ref{1158}. Consider an infinitesimal Lorentz transformation, for which Let us write\ref{1159} are real numerical coefficients that are independent of the \( {\mit\Delta}\omega^{\,\mu\,\nu} + {\mit\Delta}\omega^{\nu\,\mu} = 0.\) \( {\mit\Delta}\omega_\mu^{~\nu}\) \ref{1161} are \( 4\times 4\) matrices. To first order in small quantities,\( \sigma_{\mu\,\nu}\)
To first order in small quantities, Equations \ref{1158}, \ref{1160}, \ref{1162}, and \ref{1163} yield
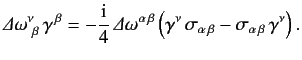
Hence, making use of the symmetry property \ref{1161}, we obtain
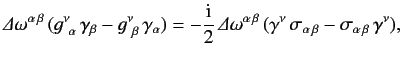
where \( {\mit\Delta}\omega^{\alpha\,\beta}\) , we deduce that
Callstack:
at (Under_Construction/Purgatory/Book:_Quantum_Mechanics_(Fitzpatrick)/11:_Relativistic_Electron_Theory/11.3:_Lorentz_Invariance_of_Dirac_Equation), /content/body/tr[12]/td[1]/span, line 1, column 1
Hence,
Now that we have found the correct transformation rules for an infinitesimal Lorentz transformation, we can easily find those for a finite transformation by building it up from a large number of successive infinitesimal transforms.
Making use of \ref{1127}, as well as \( A^\dag = 1-\frac{1}{8}\,\gamma^0\,[\gamma_\mu,\gamma_\nu]\,\gamma^0\,{\mit\Delta}\omega^{\,\mu\,\nu} = \gamma^0\,A^{-1}\,\gamma^0.\) Hence, \ref{1158} yields or where the \( j^{\,\mu}\) transform as the contravariant components of a 4-vector. Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)\ref{1171} \( \psi^\dag\,A^\dag\,\gamma^0\,\gamma^{\,\mu}\,A\,\psi= a^{\,\mu}_{~\nu}\,\psi^\dag\,\gamma^0\,\gamma^\nu\,\psi,\) \ref{1173} \( j^{\,\mu'} = a^{\,\mu}_{~\nu}\,j^{\,\nu},\) \ref{1175} Contributors


