8.5: Relative Velocity and the Coefficient of Restitution
- Page ID
- 63888
An interesting property of elastic collisions can be disclosed from a careful study of figures \(\PageIndex{1}\) and \(\PageIndex{2}\). In both cases, as you can see, the relative velocity of the two objects colliding has the same magnitude (but opposite sign) before and after the collision. In other words: in an elastic collision, the objects end up moving apart at the same rate as they originally came together.
Recall that, in Chapter 4, we defined the velocity of object 2 relative to object 1 as the quantity
\[ v_{12}=v_{2}-v_{1} \label{eq:4.3} \]
(compare Equation (4.3.8); and similarly the velocity of object 1 relative to object 2 is \(v_{21} = v_1 − v_2\). With this definition you can check that, indeed, the collisions shown in Figs. (8.1.1) and (8.1.2) satisfy the equality
\[ v_{12, i}=-v_{12, f} \label{eq:4.4} \]
(note that we could equally well have used \(v_{21}\) instead of \(v_{12}\)). For instance, in Figure (8.1.1), \(v_{12,i} = v_{2i} − v_{1i}\) = −1 m/s, whereas \(v_{12,f}\) = 2/3 − (−1/3) = 1 m/s. So the objects are initially moving towards each other at a rate of 1 m per second, and they end up moving apart just as fast, at 1 m per second. Visually, you should notice that the distance between the red and blue curves is the same before and after (but not during) the collision; the fact that they cross accounts for the difference in sign of the relative velocity, which in turns means simply that before the collision they were coming together, and afterwards they are moving apart.
It takes only a little algebra to show that Equation (\ref{eq:4.4}) follows from the joint conditions of conservation of momentum and conservation of kinetic energy. The first one (\(p_i\) = \(p_f\) ) clearly has the form
\[ m_{1} v_{1 i}+m_{2} v_{2 i}=m_{1} v_{1 f}+m_{2} v_{2 f} \label{eq:4.5} \]
whereas the second one (\(K_i\) = \(K_f\) ) can be written as
\[ \frac{1}{2} m_{1} v_{1 i}^{2}+\frac{1}{2} m_{2} v_{2 i}^{2}=\frac{1}{2} m_{1} v_{1 f}^{2}+\frac{1}{2} m_{2} v_{2 f}^{2} \label{eq:4.6} .\]
We can cancel out all the factors of 1/2 in Equation (\ref{eq:4.6})2, then rearrange it so that quantities belonging to object 1 are on one side, and quantities belonging to object 2 are on the other. We get
\begin{array}{c}
{m_{1}\left(v_{1 i}^{2}-v_{1 f}^{2}\right)=-m_{2}\left(v_{2 i}^{2}-v_{2 f}^{2}\right)} \\
{m_{1}\left(v_{1 i}-v_{1 f}\right)\left(v_{1 i}+v_{1 f}\right)=-m_{2}\left(v_{2 i}-v_{2 f}\right)\left(v_{2 i}+v_{2 f}\right)} \label{eq:4.7}
\end{array}
(using the fact that \(a^2 − b^2 = (a + b)(a − b) \)). Note, however, that Equation (\ref{eq:4.5}) can also be rewritten as
\[ m_{1}\left(v_{1 i}-v_{1 f}\right)=-m_{2}\left(v_{2 i}-v_{2 f}\right) \nonumber .\]
This immediately allows us to cancel out the corresponding factors in Eq (\ref{eq:4.7}), so we are left with \(v_{1i} + v_{1f} = v_{2i} + v_{2f} \), which can be rewritten as
\[ v_{1 f}-v_{2 f}=v_{2 i}-v_{1 i} \label{eq:4.8} \]
and this is equivalent to (\ref{eq:4.4})
So, in an elastic collision the speed at which the two objects move apart is the same as the speed at which they came together, whereas, in what is clearly the opposite extreme, in a totally inelastic collision the final relative speed is zero—the objects do not move apart at all after they collide. This suggests that we can quantify how inelastic a collision is by the ratio of the final to the initial magnitude of the relative velocity. This ratio is denoted by \(e\) and is called the coefficient of restitution. Formally,
\[ e=-\frac{v_{12, f}}{v_{12, i}}=-\frac{v_{2 f}-v_{1 f}}{v_{2 i}-v_{1 i}} \label{eq:4.9} .\]
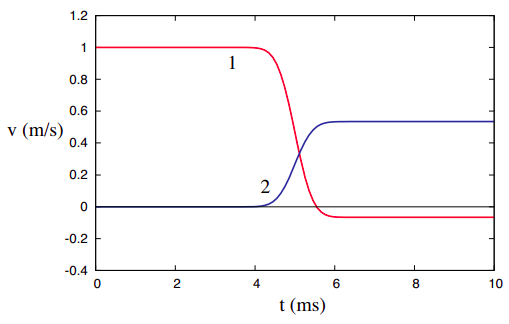
For an elastic collision, \(e\) = 1, as required by Equation (\ref{eq:4.4}). For a totally inelastic collision, like the one depicted in Figure (8.1.3), \(e\) = 0. For a collision that is inelastic, but not totally inelastic, \(e\) will have some value in between these two extremes. This knowledge can be used to “design” inelastic collisions (for homework problems, for instance!): just pick a value for \(e\), between 0 and 1, in Equation (\ref{eq:4.9}), and combine this equation with the conservation of momentum requirement (\ref{eq:4.5}). The two equations then allow you to calculate the final velocities for any values of \(m_1\), \(m_2\), and the initial velocities. Figure \(\PageIndex{4}\) below, for example, shows what the collision in Figure \(\PageIndex{1}\) would have been like, if the coefficient of restitution had been 0.6 instead of 1. You can check, by solving (\ref{eq:4.5}) and (\ref{eq:4.9}) together, and using the initial velocities, that \(v_{1f}\) = −1/15 m/s = −0.0667 m/s, and \(v_{2f}\) = 8/15 m/s = 0.533 m/s.
Although, as I just mentioned, for most “normal” collisions the coefficient of restitution will be a positive number between 1 and 0, there can be exceptions to this. If one of the objects passes through the other (like a bullet through a target, for instance), the value of \(e\) will be negative (although still between 0 and 1 in magnitude). And \(e\) can be greater than 1 for so-called “explosive collisions,” where some amount of extra energy is released, and converted into kinetic energy, as the objects collide. (For instance, two hockey players colliding on the rink and pushing each other away.) In this case, the objects may well fly apart faster than they came together.
An extreme example of a situation with \(e\) > 0 is an explosive separation, which is when the two objects are initially moving together and then fly apart. In that case, the denominator of Equation (\ref{eq:4.9}) is zero, and so \(e\) is formally infinite. This suggests, what is in fact the case, namely, that although explosive processes are certainly important, describing them through the coefficient of restitution is rare, even when it would be formally possible. In practice, use of the coefficient of restitution is mostly limited to the elastic-to-completely inelastic range, that is, 0 ≤ \(e\) ≤ 1.
2You may be wondering, just why do we define kinetic energy with a factor 1/2 in front, anyway? There is no good answer at this point. Let’s just say it will make the definition of “potential energy” simpler later, particularly as regards its relationship to force.


