22.4: Newton’s Second Law for Rotation

In this subsection, we put together all the pieces learned so far in this chapter to analyze the dynamics of rotating rigid bodies. We have analyzed motion with kinematics and rotational kinetic energy but have not yet connected these ideas with force and/or torque. In this subsection, we introduce the rotational equivalent to Newton’s second law of motion and apply it to rigid bodies with fixed-axis rotation.

Newton’s Second Law for Rotation

We have thus far found many counterparts to the translational terms used throughout this text, most recently, torque, the rotational analog to force. This raises the question: Is there an analogous equation to Newton’s second law, \(\sum \vec{F}\) = m\(\vec{a}\), which involves torque and rotational motion? To investigate this, we start with Newton’s second law for a single particle rotating around an axis and executing circular motion. Let’s exert a force \(\vec{F}\) on a point mass m that is at a distance r from a pivot point (Figure \(\PageIndex{1}\)). The particle is constrained to move in a circular path with fixed radius and the force is tangent to the circle. We apply Newton’s second law to determine the magnitude of the acceleration a = \(\frac{F}{m}\) in the direction of \(\vec{F}\). Recall that the magnitude of the tangential acceleration is proportional to the magnitude of the angular acceleration by a = r\(\alpha\). Substituting this expression into Newton’s second law, we obtain

\[F = mr \alpha \ldotp\]

Figure \(\PageIndex{1}\): An object is supported by a horizontal frictionless table and is attached to a pivot point by a cord that supplies centripetal force. A force \(\vec{F}\) is applied to the object perpendicular to the radius r, causing it to accelerate about the pivot point. The force is perpendicular to r.

Multiply both sides of this equation by r,

\[rF = mr^{2} \alpha \ldotp\]

Note that the left side of this equation is the torque about the axis of rotation, where r is the lever arm and F is the force, perpendicular to r. Recall that the moment of inertia for a point particle is I = mr². The torque applied perpendicularly to the point mass in Figure \(\PageIndex{1}\) is therefore

\[\tau = I \alpha \ldotp\]

The torque on the particle is equal to the moment of inertia about the rotation axis times the angular acceleration. We can generalize this equation to a rigid body rotating about a fixed axis.

Newton’s Second Law for Rotation

If more than one torque acts on a rigid body about a fixed axis, then the sum of the torques equals the moment of inertia times the angular acceleration:

\[\sum_{i} \tau_{i} = I \alpha \ldotp \label{10.25}\]

The term I\(\alpha\) is a scalar quantity and can be positive or negative (counterclockwise or clockwise) depending upon the sign of the net torque. Remember the convention that counterclockwise angular acceleration is positive. Thus, if a rigid body is rotating clockwise and experiences a positive torque (counterclockwise), the angular acceleration is positive.

Equation \ref{10.25} is Newton’s second law for rotation and tells us how to relate torque, moment of inertia, and rotational kinematics. This is called the equation for rotational dynamics. With this equation, we can solve a whole class of problems involving force and rotation. It makes sense that the relationship for how much force it takes to rotate a body would include the moment of inertia, since that is the quantity that tells us how easy or hard it is to change the rotational motion of an object.

Deriving Newton’s Second Law for Rotation in Vector Form

As before, when we found the angular acceleration, we may also find the torque vector. The second law \(\sum \vec{F}\) = m\(\vec{a}\) tells us the relationship between net force and how to change the translational motion of an object. We have a vector rotational equivalent of this equation, which can be found by using Equation 10.2.10 and Figure 10.2.7. Equation 10.2.10 relates the angular acceleration to the position and tangential acceleration vectors:

\[\vec{a} = \vec{\alpha} \times \vec{r} \ldotp\]

We form the cross product of this equation with \(\vec{r}\) and use a cross product identity (note that \(\vec{r}\; \cdotp \vec{\alpha}\) = 0):

\[\vec{r} \times \vec{a} = \vec{r} \times (\vec{\alpha} \times \vec{r}) = \vec{\alpha} (\vec{r}\; \cdotp \vec{r}) - \vec{r} (\vec{r}\; \cdotp \vec{\alpha}) = \vec{\alpha} (\vec{r}\; \cdotp \vec{r}) = \vec{\alpha} r^{2} \ldotp\]

We now form the cross product of Newton’s second law with the position vector \(\vec{r}\),

\[\sum (\vec{r} \times \vec{F}) = \vec{r} \times (m \vec{a}) = m \vec{r} \times \vec{a} = mr^{2} \vec{\alpha} \ldotp\]

Identifying the first term on the left as the sum of the torques, and mr² as the moment of inertia, we arrive at Newton’s second law of rotation in vector form:

\[\sum \tau = I \alpha \ldotp \label{10.26}\]

This equation is exactly Equation \ref{10.25} but with the torque and angular acceleration as vectors. An important point is that the torque vector is in the same direction as the angular acceleration.

Applying the Rotational Dynamics Equation

Before we apply the rotational dynamics equation to some everyday situations, let’s review a general problem-solving strategy for use with this category of problems.

Problem-Solving Strategy: Rotational Dynamics

1. Examine the situation to determine that torque and mass are involved in the rotation. Draw a careful sketch of the situation.
2. Determine the system of interest.
3. Draw a free-body diagram. That is, draw and label all external forces acting on the system of interest.
4. Identify the pivot point. If the object is in equilibrium, it must be in equilibrium for all possible pivot points––chose the one that simplifies your work the most.
5. Apply \(\sum_{i} \tau_{i} = I \alpha\), the rotational equivalent of Newton’s second law, to solve the problem. Care must be taken to use the correct moment of inertia and to consider the torque about the point of rotation.
6. As always, check the solution to see if it is reasonable.

Example 10.16: Calculating the Effect of Mass Distribution on a Merry-Go-Round

Consider the father pushing a playground merry-go-round in Figure \(\PageIndex{2}\). He exerts a force of 250 N at the edge of the 200.0-kg merry-go-round, which has a 1.50-m radius. Calculate the angular acceleration produced (a) when no one is on the merry-go-round and (b) when an 18.0-kg child sits 1.25 m away from the center. Consider the merry-go-round itself to be a uniform disk with negligible friction.

Figure \(\PageIndex{2}\): A father pushes a playground merry-go-round at its edge and perpendicular to its radius to achieve maximum torque.

Strategy

The net torque is given directly by the expression \(\sum_{i} \tau_{i} = I \alpha\), To solve for \(\alpha\), we must first calculate the net torque \(\tau\) (which is the same in both cases) and moment of inertia I (which is greater in the second case).

Solution

1. The moment of inertia of a solid disk about this axis is given in Figure 10.5.4 to be \(\frac{1}{2} MR^{2} \ldotp\). We have M = 50.0 kg and R = 1.50 m, so
   \[I = (0.500)(50.0\; kg)(1.50\; m)^{2} = 56.25\; kg\; \cdotp m^{2} \ldotp\]
   To find the net torque, we note that the applied force is perpendicular to the radius and friction is negligible, so that
   \[\tau = rF \sin \theta = (1.50\; m)(250.0\; N) - 375.0\; N\; \cdotp m \ldotp\]
   Now, after we substitute the known values, we find the angular acceleration to be
   \[\alpha = \frac{\tau}{I} = \frac{375.0\; N\; \cdotp m}{56.25\; kg\; \cdotp m^{2}} = 6.67\; rad/s^{2} \ldotp
2. We expect the angular acceleration for the system to be less in this part because the moment of inertia is greater when the child is on the merry-go-round. To find the total moment of inertia I, we first find the child’s moment of inertia I_c by approximating the child as a point mass at a distance of 1.25 m from the axis. Then
   \[I_{c} = mR^{2} = (18.0\; kg)(1.25\; m)^{2} = 28.13\; kg\; \cdotp m^{2} \ldotp\]
   The total moment of inertia is the sum of the moments of inertia of the merry-go-round and the child (about the same axis):
   \[I = (28.13\; kg\; \cdotp m^{2}) + (56.25\; kg\; \\]cdotp m^{2}) = 84.38\; kg\; \cdotp m^{2} \ldotp\]
   Substituting known values into the equation for \(\alpha\) gives
   \[\alpha =\frac{\tau}{I} = \frac{375.0\; N\; \cdotp m}{84.38\; kg\; \cdotp m^{2}} = 4.44\; rad/s \ldotp\]

Significance

The angular acceleration is less when the child is on the merry-go-round than when the merry-go-round is empty, as expected. The angular accelerations found are quite large, partly due to the fact that friction was considered to be negligible. If, for example, the father kept pushing perpendicularly for 2.00 s, he would give the merry-goround an angular velocity of 13.3 rad/s when it is empty but only 8.89 rad/s when the child is on it. In terms of revolutions per second, these angular velocities are 2.12 rev/s and 1.41 rev/s, respectively. The father would end up running at about 50 km/h in the first case.

Exercise 10.7

The fan blades on a jet engine have a moment of inertia 30.0 kg • m². In 10 s, they rotate counterclockwise from rest up to a rotation rate of 20 rev/s. (a) What torque must be applied to the blades to achieve this angular acceleration? (b) What is the torque required to bring the fan blades rotating at 20 rev/s to a rest in 20 s?

 

We do not actually need the force of static friction to keep an object rolling on a flat surface (as I mentioned above, the motion could in principle go on “unforced” forever), but things are different on an inclined plane. Figure \(\PageIndex{2}\) shows an object rolling down an inclined plane, and the corresponding extended free-body diagram.

Figure \(\PageIndex{2}\): An object rolling down an inclined plane, and the extended free-body diagram. Note that neither gravity (applied at the CM) nor the normal force (whose line of action passes through the CM) exert a torque around the center of mass; only the force of static friction, \(\vec F^s\), does.

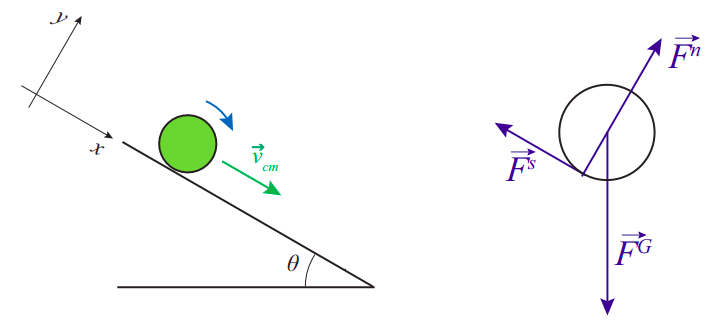
The basic equations we use to solve for the object’s motion are the sum of forces equation:

\[ \sum \vec{F}_{e x t}=M \vec{a}_{c m} \label{eq:9.35} \]

the net torque equation, with torques taken around the center of mass^.

\[ \sum \vec{\tau}_{e x t}=I \vec{\alpha} \label{eq:9.36} \]

and the extension of the condition of rolling without slipping, (11.2.1), to the accelerations:

\[ \left|a_{c m}\right|=R|\alpha| \label{eq:9.37}.\]

For the situation shown in Figure \(\PageIndex{2}\), if we take down the plane as the positive direction for linear motion, and clockwise torques as negative, we have to write \(a_{cm} = −R\alpha\). In the direction perpendicular to the plane, we conclude from (\ref{eq:9.35}) that \(F^n = Mg \cos \theta\), an equation we will not actually need; in the direction along the plane, we have

\[ M a_{c m}=M g \sin \theta-F^{s} \label{eq:9.38} \]

and the torque equation just gives \(−F^sR = I\alpha\), which with \(a_{cm} = −R\alpha\) becomes

\[ F^{s} R=I \frac{a_{c m}}{R} \label{eq:9.39} .\]

We can eliminate \(F^s\) in between these two equations and solve for \(a_{cm}\):

\[ a_{c m}=\frac{g \sin \theta}{1+I /\left(M R^{2}\right)} \label{eq:9.40} .\]

Now you can see why, earlier in the semester, we were always careful to assume that all the objects we sent down inclined planes were sliding, not rolling! The acceleration for a rolling object is never equal to simply \(g \sin \theta\). Most remarkably, the correction factor depends only on the shape of the rolling object, and not on its mass or size, since the ratio of \(I\) to \(MR^2\) is independent of \(m\) and \(R\) for any given geometry. Thus, for instance, for a disk, \(I = \frac{1}{2}MR^2\), so \(a_{cm} = \frac{2}{3} g \sin \theta\), whereas for a hoop, \(I = MR^2\), so \(a_{cm} = \frac{1}{2} g \sin \theta\). So any disk or solid cylinder will always roll down the incline faster than any hoop or hollow cylinder, regardless of mass or size.

This rather surprising result may be better understood in terms of energy. First, let's show (a result that is somewhat overdue) that for a rigid object that is rotating around an axis passing through its center of mass with angular velocity \(\omega\) we can write the total kinetic energy as

\[ K=K_{c m}+K_{r o t}=\frac{1}{2} M v_{c m}^{2}+\frac{1}{2} I \omega^{2} \label{eq:9.41} .\]

This is because for every particle the velocity can be written as \(\vec{v}=\vec{v}_{c m}+\vec{v}^{\prime}\), where \(\vec{v}^{\prime}\) is the velocity relative to the center of mass (that is, in the CM frame). Since in this frame the motion is a simple rotation, we have \( \left|v^{\prime}\right|=\omega r \), where \(r\) is the particle’s distance to the axis. Therefore, the kinetic energy of that particle will be

\begin{align}
\frac{1}{2} m v^{2}=\frac{1}{2} \vec{v} \cdot \vec{v} &=\frac{1}{2} m\left(\vec{v}_{c m}+\vec{v}^{\prime}\right) \cdot\left(\vec{v}_{c m}+\vec{v}^{\prime}\right) \nonumber \\
&=\frac{1}{2} m v_{c m}^{2}+\frac{1}{2} m v^{\prime 2}+m \vec{v}_{c m} \cdot \vec{v}^{\prime} \nonumber \\
&=\frac{1}{2} m v_{c m}^{2}+\frac{1}{2} m r^{2} \omega^{2}+\vec{v}_{c m} \cdot \vec{p}^{\prime} \label{eq:9.42}
\end{align}

(Note how I have made use of the dot product to calculate the magnitude squared of a vector.) On the last line, the quantity \(\vec{p}^{\prime}\) is the momentum of that particle in the CM frame. Adding those momenta for all the particles should give zero, since, as we saw in an earlier chapter, the center of mass frame is the zero momentum frame. Then, adding the contributions of all particles to the first and second terms in \ref{eq:9.42} gives Equation (\ref{eq:9.41}).