23.5: Examples

Example \(\PageIndex{1}\): Oscillator in a box (a basic accelerometer!)

Consider a block-spring system inside a box, as shown in the figure. The block is attached to the spring, which is attached to the inside wall of the box. The mass of the block is 0.2 kg. For parts (a) through (f), assume that the box does not move.

Suppose you pull the block 10 cm to the right and release it. The angular frequency of the oscillations is 30 rad/s. Neglect friction between the block and the bottom of the box.

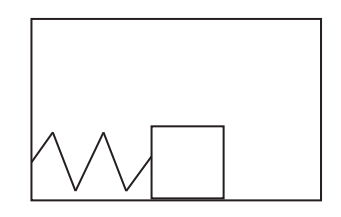
1. What is the spring constant?
2. What will be the amplitude of the oscillations?
3. Taking to the right to be positive, at what point in the oscillation is the velocity minimum and what is its minimum value?
4. At what point in the oscillation is the acceleration minimum, and what is its minimum value?
5. What is the total energy of the spring-block system?
6. If you take \(t\) = 0 to be the instant when you release the block, write an equation of motion for the oscillation, \(x(t)\) = ?, identifying the values of all constants that you use.
7. Imagine now that the box, with the spring and block in it, starts moving to the left with an acceleration \(a\) = −4 m/s². By how much does the equilibrium position of the block shift (relative to the box), and in what direction?

Solution

Most of this is really pretty straightforward, since it is just a matter of using the equations introduced in this chapter properly:

(a) Since we know that for this kind of situation, the angular frequency, the mass and the spring constant are related by

\[ \omega=\sqrt{\frac{k}{m}} \nonumber \]

we con solve this for \(k\):

\[ k=m \omega^{2}=0.2 \: \mathrm{kg} \times\left(30 \: \frac{\mathrm{rad}}{\mathrm{s}}\right)^{2}=180 \: \frac{\mathrm{N}}{\mathrm{m}} \nonumber \]

(b) The amplitude will be 10 cm, since it is released at that point with no kinetic energy.

(c) The velocity is minimum (largest in magnitude, but with a negative sign) as the object passes through the equilibrium position moving to the left.

\[ v_{\min }=-\omega A=-\left(30 \: \frac{\mathrm{rad}}{\mathrm{s}}\right) \times 0.1 \: \mathrm{m}=-3 \: \frac{\mathrm{m}}{\mathrm{s}} \nonumber \]

(d) The acceleration is minimum (again, largest in magnitude, but with a negative sign) when the spring is maximally stretched (block is farthest to the right), since this gives you the maximal force in the negative direction:

\[ a_{\min }=-\omega^{2} A=-\left(30 \: \frac{\mathrm{rad}}{\mathrm{s}}\right)^{2} \times 0.1 \: m=-90 \: \frac{\mathrm{m}}{\mathrm{s}^{2}} \nonumber \]

(e) The total energy is given by the formula (either one is acceptable)

\[ E=\frac{1}{2} m \omega^{2} A^{2}=\frac{1}{2} k A^{2}=\frac{1}{2}(180 \: \mathrm{N} / \mathrm{m}) \times(0.1 \: \mathrm{m})^{2}=0.9 \: \mathrm{J} \nonumber \]

(You could also use \(E = \frac{1}{2}mv^{2}_{max}\).)

(f) The result is

\[ x(t)=A \cos (\omega t)=A \sin \left(\omega t+\frac{\pi}{2}\right) \nonumber \]

with \(A\) = 0.1 m and \(\omega\) = 30 rad/s. You could also just write the numbers directly in the formula, but in that case you need to include the units implicitly or explicitly. What I mean by “implicitly” is to say something like: “\(x(t)=0.1 \cos(30t)\), with \(x\) in meters and \(t\) in seconds.”

(g) The equilibrium position is where the block could sit at rest relative to the box. In that case, relative to the ground outside the box, it would be moving with an acceleration \(a\) = −4 m/s², and the spring force (which is the only actual force acting on the block) would have to provide this acceleration:

\[ F_{x}^{s p r}=-k \Delta x=m a \nonumber \]

so

\[ \Delta x=-\frac{m a}{k}=\frac{0.2 \: k g \times 4 \: m / s^{2}}{180 \: N / m}=0.00444 \: m \nonumber \]

or 4.44 mm. This is positive, so the spring stretches—the equilibrium position for the block is shifted to the right, relative to the box’s walls.

Another way to see this is the following. As we saw in example 20.3.4, an accelerated reference system, with acceleration a, appears “from the inside” as an inertial reference system subject to a gravitational interaction that pulls any object with mass \(m\) with a force equal to \(ma\) in the direction opposite the acceleration. Therefore, inside the box, which is accelerating towards the left, the block behaves as if there was a force of gravity of magnitude \(ma\), pulling it to the right. In other words, we have a situation like the one illustrated in Figure 11.2.5, only sideways. As in that case, we find the equilibrium position is shifted just enough for the force of the stretched spring to match the “force of gravity,” and in this way we get again the equation \(F^{spr}_{x} = ma\).

To get an accelerometer, we provide the box with some readout mechanism that can tell us the change in the oscillator’s equilibrium position. This basic principle is one of the ways accelerometers— and so-called “inertial navigation systems”—work.

Example \(\PageIndex{2}\): Meter stick as a physical pendulum

While working on the lab on torques, you notice that a meter stick suspended from the middle behaves a little like a pendulum, in that it performs very slow oscillations when you tilt it slightly. Intrigued, you notice that it is suspended by a simple loop of string tied in a knot at the top (see figure). You measure the period of the oscillations to be about 5 s, and the width of the stick to be about 2.5 cm.

1. What does this tell you about the quantity \(I/M\), where \(M\) is the mass of the stick, and \(I\) its moment of inertia around a certain point?
2. What is the “certain point” mentioned in (a)?

Solution

As the picture below shows, the stick will behave like a physical pendulum, oscillating around the point of suspension O, which in this case is just next to the stick, where the knot is. As seen in the blown-up detail, if the width of the stick is w, the center of mass of the stick is located a distance \(d = w/2\) away from the point of suspension:

As shown in Section 23.3, we have then

\[ \omega=\sqrt{\frac{M g w}{2 I}} \label{eq:11.30} .\]

Squaring this, and solving for \(I/M\),

\[ \frac{I}{M}=\frac{g w}{2 \omega^{2}}=\frac{9.8 \: \mathrm{m} / \mathrm{s}^{2} \times 0.025 \: \mathrm{m}}{2 \times(2 \pi / 5 \: \mathrm{s})^{2}}=0.0776 \: \mathrm{m}^{2} \label{eq:11.31} .\]

The moment of inertia is to be calculated around the point O, that is to say, the point of suspension (where the knot is in the figure). For reference, the moment of inertia of a thin rod of length \(l\) around its midpoint is \(Ml^2/12 = 0.083l^2\). The length of the meter stick is, of course, 1 m, so the result \(I/M\) ∼ 0.08 m² obtained above seems reasonable.

Exercise \(\PageIndex{3}\)

A block of mass \(m\) is sliding on a frictionless, horizontal surface, with a velocity \(v_i\). It hits an ideal spring, of spring constant \(k\), which is attached to the wall. The spring compresses until the block momentarily stops, and then starts expanding again, so the block ultimately bounces off.

1. Write down an equation of motion (a function \(x(t)\)) for the block, which is valid for as long as it is in contact with the spring. For simplicity, assume the block is initially moving to the right, take the time when it first makes contact with the spring to be \(t\) = 0, and let the position of the block at that time to be \(x\) = 0. Make sure that you express any constants in your equation (such as \(A\) or \(\omega\)) in terms of the given data, namely, \(m\), \(v_i\), and \(k\).
2. Sketch the function \(x(t)\) for the relevant time interval.

Exercise \(\PageIndex{4}\)

For this problem, imagine that you are on a ship that is oscillating up and down on a rough sea. Assume for simplicity that this is simple harmonic motion (in the vertical direction) with amplitude 5 cm and frequency 2 Hz. There is a box on the floor with mass \(m\) = 1 kg.

1. Assuming the box remains in contact with the floor throughout, find the maximum and minimum values of the normal force exerted on it by the floor over an oscillation cycle.
2. How large would the amplitude of the oscillations have to become for the box to lose contact with the floor, assuming the frequency remains constant? (Hint: what is the value of the normal force at the moment the box loses contact with the floor?)

Exercise \(\PageIndex{5}\)

Imagine a simple pendulum swinging in an elevator. If the cable holding the elevator up was to snap, allowing the elevator to go into free fall, what would happen to the frequency of oscillation of the pendulum? Justify your answer.

Exercise \(\PageIndex{6}\)

Consider a block of mass \(m\) attached to two springs, one on the left with spring constant \(k_1\) and one on the right with spring constant \(k_2\). Each spring is attached on the other side to a wall, and the block slides without friction on a horizontal surface. When the block is sitting at \(x\) = 0, both springs are relaxed.

Write Newton’s second law, \(F = ma\), as a differential equation for an arbitrary position \(x\) of the block. What is the period of oscillation of this system?

Exercise \(\PageIndex{7}\)

Consider the block hanging from a spring shown in Figure 23.2.5. Suppose the mass of the block is 1.5 kg and the system is at rest when the spring has been stretched 2 cm from its original length (that is, with reference to the figure, \(y_{0}-y_{0}^{\prime}\) = 0.02 m).

1. What is the value of the spring constant \(k\)?
2. If you stretch the spring by an additional 2 cm downward from this equilibrium position, and release it, what will be the frequency of the oscillations?
3. Now consider the system formed by the spring, the block, and the earth. Take the “zero” of gravitational potential energy to be at the height \(y_{0}^{\prime}\) (the equilibrium point; you may also use this as the origin for the vertical coordinate!), and calculate all the energies in the system (kinetic, spring/elastic, and gravitational) at the highest point in the oscillation, the equilibrium point, and the lowest point. Verify that the sum is indeed constant.