8.1: History and Quantum Mechanical Quantities
- Last updated
- Save as PDF
- Page ID
- 17128
learning objectives
- Explain how the photoelectric effect paradox was solved by Albert Einstein.
Electrons are emitted from matter when light shines on a surface . This is called the photoelectric effect, and the electrons emitted in this manner are called photoelectrons.
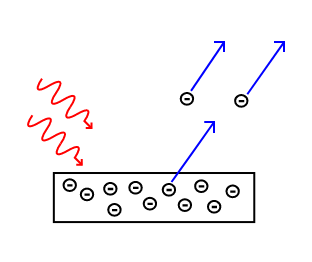
The Photoelectric Effect: Electrons are emitted from matter by absorbed light.
The photoelectric effect typically requires photons with energies from a few electronvolts to 1 MeV for heavier elements, roughly in the ultraviolet and X-ray range. Study of the photoelectric effect led to important steps in understanding the quantum nature of light and electrons and influenced the formation of the concept of wave-particle duality. The photoelectric effect is also widely used to investigate electron energy levels in matter.
Photoelectric Effect: A brief introduction to the Photoelectric Effect and electron photoemission.
Heinrich Hertz discovered the photoelectric effect in 1887. Although electrons had not been discovered yet, Hertz observed that electric currents were produced when ultraviolet light was shined on a metal. By the beginning of the 20th century, physicists confirmed that:
- The energy of the individual photoelectrons increased with the frequency (or color) of the light, but was independent of the intensity (or brightness) of the radiation.
- The photoelectric current was determined by the light’s intensity; doubling the intensity of the light doubled the number of emitted electrons.
This observation was very puzzling to many physicists. At the time, light was accepted as a wave phenomenon. Since energy carried by a wave should only depend on its amplitude (and not on the frequency of the wave), the frequency dependence of the emitted electrons’ energies didn’t make sense.
In 1905, Albert Einstein solved this apparent paradox by describing light as composed of discrete quanta (now called photons), rather than continuous waves. Building on Max Planck’s theory of black body radiation, Einstein theorized that the energy in each quantum of light was equal to the frequency multiplied by a constant h, later called Planck’s constant. A photon above a threshold frequency has the required energy to eject a single electron, creating the observed effect. As the frequency of the incoming light increases, each photon carries more energy, hence increasing the energy of each outgoing photoelectron. By doubling the number of photons as the intensity is doubled, the number of photelectrons should double accordingly.
According to Einstein, the maximum kinetic energy of an ejected electron is given by \(\mathrm{K_{max}=hf−ϕ}\), where \(\mathrm{h}\) is the Planck constant and f is the frequency of the incident photon. The term \(ϕ\) is known as the work function, the minimum energy required to remove an electron from the surface of the metal. The work function satisfies \(\mathrm{ϕ=hf_0}\), where \(\mathrm{f_0}\) is the threshold frequency for the metal for the onset of the photoelectric effect. The value of work function is an intrinsic property of matter.
Is light then composed of particles or waves? Young’s experiment suggested that it was a wave, but the photoelectric effect indicated that it should be made of particles. This question would be resolved by de Broglie: light, and all matter, have both wave-like and particle-like properties.
Photon Energies of the EM Spectrum
The electromagnetic (EM) spectrum is the range of all possible frequencies of electromagnetic radiation.
learning objectives
- Compare photon energy with the frequency of the radiation
The Electromagnetic Spectrum
The electromagnetic (EM) spectrum is the range of all possible frequencies of electromagnetic radiation . The electromagnetic spectrum extends from below the low frequencies used for modern radio communication to gamma radiation at the short-wavelength (high-frequency) end, thereby covering wavelengths of thousands of kiilometers down to those of a fraction of the size of an atom (approximately an angstrom). The limit for long wavelengths is the size of the universe itself.
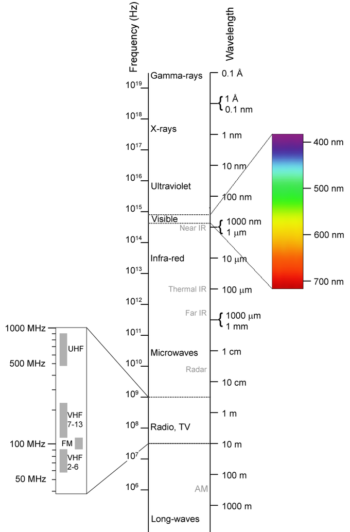
Electromagnetic spectrum: This shows the electromagnetic spectrum, including the visible region, as a function of both frequency (left) and wavelength (right).
Maxwell’s equations predicted an infinite number of frequencies of electromagnetic waves, all traveling at the speed of light. This was the first indication of the existence of the entire electromagnetic spectrum. Maxwell’s predicted waves included waves at very low frequencies compared to infrared, which in theory might be created by oscillating charges in an ordinary electrical circuit of a certain type. In 1886, the physicist Hertz built an apparatus to generate and detect what are now called radio waves, in an attempt to prove Maxwell’s equations and detect such low-frequency electromagnetic radiation. Hertz found the waves and was able to infer (by measuring their wavelength and multiplying it by their frequency) that they traveled at the speed of light. Hertz also demonstrated that the new radiation could be both reflected and refracted by various dielectric media, in the same manner as light.
Filling in the Electromagnetic Spectrum
In 1895, Wilhelm Röntgen noticed a new type of radiation emitted during an experiment with an evacuated tube subjected to a high voltage. He called these radiations ‘X-rays’ and found that they were able to travel through parts of the human body but were reflected or stopped by denser matter such as bones. Before long, there were many new uses for them in the field of medicine.
The last portion of the electromagnetic spectrum was filled in with the discovery of gamma rays. In 1900, Paul Villard was studying the radioactive emissions of radium when he identified a new type of radiation that he first thought consisted of particles similar to known alpha and beta particles, but far more penetrating than either. However, in 1910, British physicist William Henry Bragg demonstrated that gamma rays are electromagnetic radiation, not particles. In 1914, Ernest Rutherford (who had named them gamma rays in 1903 when he realized that they were fundamentally different from charged alpha and beta rays) and Edward Andrade measured their wavelengths, and found that gamma rays were similar to X-rays, but with shorter wavelengths and higher frequencies.
The relationship between photon energy and the radiation’s frequency and wavelength is illustrated as the following equilavent equation: \(\nu = \frac { c } { \lambda }\), or \(\nu = \mathrm{\frac { E } { h }}\) or \(\mathrm { E } = \frac { \mathrm { hc } } { \lambda }\) where νν is the frequency, \(\mathrm{λ}\) is the wavelength, \(\mathrm{E}\) is photon energy, \(\mathrm{c}\) is the speed of light, and hh is the Planck constant. Generally, electromagnetic radiation is classified by wavelength into radio waves, microwaves, terahertz (or sub-millimeter) radiation, infrared, the visible region humans perceive as light, ultraviolet, X-rays, and gamma rays. The behavior of EM radiation depends on its wavelength. When EM radiation interacts with single atoms and molecules, its behavior also depends on the amount of energy per quantum (photon) it carries.
Most parts of the electromagnetic spectrum are used in science for spectroscopic and other probing interactions as ways to study and characterize matter. Also, radiation from various parts of the spectrum has many other uses in communications and manufacturing.
Energy, Mass, and Momentum of Photon
A photon is an elementary particle, the quantum of light, which carries momentum and energy.
learning objectives
- State physical properties of a photon
A photon is an elementary particle, the quantum of light. It has no rest mass and has no electric charge. The modern photon concept was developed gradually by Albert Einstein to explain experimental observations of the photoelectric effect, which did not fit the classical wave model of light. In particular, the photon model accounted for the frequency dependence of light’s energy. Max Planck explained black body radiation using semiclassical models, in which light is still described by Maxwell’s equations, but the material objects that emit and absorb light, do so in amounts of energy that are quantized.
Photons are emitted in many natural processes. They are emitted from light sources such as floor lamps or lasers . For example, when a charge is accelerated it emits photons, a phenomenon known as synchrotron radiation. During a molecular, atomic or nuclear transition to a lower or higher energy level, photons of various energy will be emitted or absorbed respectively. A photon can also be emitted when a particle and its corresponding antiparticle are annihilated. During all these processes, photons will carry energy and momentum.

laser: Photons emitted in a coherent beam from a laser.
Energy of photon: From the studies of photoelectric effects, energy of a photon is directly proportional to its frequency with the Planck constant being the proportionality factor. Therefore, we already know that \(\mathrm { E } = \mathrm { h } \nu\) (Eq. 1), where \(\mathrm{E}\) is the energy and νν is the frequency.
Momentum of photon: According to the theory of Special Relativity, energy and momentum (p) of a particle with rest mass m has the following relationship: \(\mathrm { E } ^ { 2 } = \left( \mathrm { mc } ^ { 2 } \right) ^ { 2 } + \mathrm { p } ^ { 2 } \mathrm { c } ^ { 2 }\), where \(\mathrm{c}\) is the speed of light. In the case of a photon with zero rest mass, we get \(\mathrm { E } = \mathrm { p c}\). Combining this with Eq. 1, we get \(\mathrm { p } = \frac { \mathrm { h } \nu } { \mathrm { c } } = \frac { \mathrm { h } } { \lambda }\). Here, \(\mathrm{λ}\) is the wavelength of the light. Since momentum is a vector quantity and p points in the direction of the photon’s propagation, we can write \(\mathrm { p } = \mathrm { h } \mathrm { k }\), where \(\mathrm { h } = \frac { \mathrm { h } } { 2 \pi }\) and is \(\mathrm{k}\) a wave vector.
You may wonder how an object with zero rest mass can have nonzero momentum. This confusion often arises because of the commonly used form of momentum (mvmv in non-relativistic mechanics and γmvγmv in relativistic mechanics, where vv is velocity and \(\gamma = \frac { 1 } { \sqrt { 1 - \frac { v ^ { 2 } } { c ^ { 2 } } } }\). ) This formula, obviously, shouldn’t be used in the case \(\mathrm{v=c}\).
Implications of Quantum Mechanics
Quantum mechanics has had enormous success in explaining microscopic systems and has become a foundation of modern science and technology.
learning objectives
- Explain importance of quantum mechanics for technology and other branches of science
The field of quantum mechanics has been enormously successful in explaining many of the features of our world. The behavior of the subatomic particles (electrons, protons, neutrons, photons, and others) that make up all forms of matter can often be satisfactorily described only using quantum mechanics. Quantum mechanics has also strongly influenced string theory.
Quantum mechanics is also critically important for understanding how individual atoms combine covalently to form molecules. The application of quantum mechanics to chemistry is known as quantum chemistry. Relativistic quantum mechanics can, in principle, mathematically describe most of chemistry. Quantum mechanics can also provide quantitative insight into ionic and covalent bonding processes by explicitly showing which molecules are energetically favorable to which other molecules and the magnitudes of the energies involved. Furthermore, most of the calculations performed in modern computational chemistry rely on quantum mechanics.
A great number of modern technological inventions operate on a scale where quantum effects are significant. Examples include the laser , the transistor (and thus the microchip), the electron microscope, and magnetic resonance imaging (MRI). The study of semiconductors led to the invention of the diode and the transistor, which are indispensable parts of modern electronic systems and devices.

Laser: Red (635-nm), green (532-nm), and blue-violet (445-nm) lasers
Researchers are currently seeking robust methods of directly manipulating quantum states. Efforts are being made to more fully develop quantum cryptography, which will theoretically allow guaranteed secure transmission of information. A more distant goal is the development of quantum computers, which are expected to perform certain computational tasks exponentially faster than classical computers. Another topic of active research is quantum teleportation, which deals with techniques to transmit quantum information over arbitrary distances.
Particle-Wave Duality
Wave–particle duality postulates that all physical entities exhibit both wave and particle properties.
learning objectives
- Describe experiments that demonstrated wave-particle duality of physical entities
Wave–particle duality postulates that all physical entities exhibit both wave and particle properties. As a central concept of quantum mechanics, this duality addresses the inability of classical concepts like “particle” and “wave” to fully describe the behavior of (usually) microscopic objects.
From a classical physics point of view, particles and waves are distinct concepts. They are mutually exclusive, in the sense that a particle doesn’t exhibit wave-like properties and vice versa. Intuitively, a baseball doesn’t disappear via destructive interference, and our voice cannot be localized in space. Why then is it that physicists believe in wave-particle duality? Because that’s how mother Nature operates, as they have learned from several ground-breaking experiments. Here is a short, chronological list of those experiments:
- Young’s double-slit experiment: In the early Nineteenth century, the double-slit experiments by Young and Fresnel provided evidence that light is a wave. In 1861, James Clerk Maxwell explained light as the propagation of electromagnetic waves according to the Maxwell’s equations.
- Black body radiation: In 1901, to explain the observed spectrum of light emitted by a glowing object, Max Planck assumed that the energy of the radiation in the cavity was quantized, contradicting the established belief that electromagnetic radiation is a wave.
- Photoelectric effect: Classical wave theory of light also fails to explain photoelectric effect. In 1905, Albert Einstein explained the photoelectric effects by postulating the existence of photons, quanta of light energy with particulate qualities.
- De Broglie’s wave (matter wave): In 1924, Louis-Victor de Broglie formulated the de Broglie hypothesis, claiming that all matter, not just light, has a wave-like nature. His hypothesis was soon confirmed with the observation that electrons (matter) also displays diffraction patterns, which is intuitively a wave property.
From these historic achievements, physicists now accept that all entities in nature behave as both a particle and a wave, depending on the specifics of the phenomena under consideration. Because of its counter-intuitive aspect, the meaning of the particle-wave duality is still a point of debate in quantum physics. The standard interpretation is that the act of measurement causes the set of probabilities, governed by a probability distribution function acquired from a “wave”, to immediately and randomly assume one of the possible values, leading to a “particle”-like result.
So, why do we not notice a baseball acting like a wave? The wavelength of the matter wave associated with a baseball, say moving at 95 miles per hour, is extremely small compared to the size of the ball so that wave-like behavior is never noticeable.
Diffraction Revisited
De Broglie’s hypothesis was that particles should show wave-like properties such as diffraction or interference.
learning objectives
- Compare application of X-ray, electron, and neutron diffraction for materials research
The de Broglie hypothesis, formulated in 1924, predicts that particles should also behave as waves. The wavelength of an electron is given by the de Broglie equation \(\mathrm{\lambda = \frac { h } { p }}\). Here \(\mathrm{h}\) is Planck’s constant and pp the relativistic momentum of the electron. \(\mathrm{λ}\) is called the de Broglie wavelength.
From the work by Planck (black body radiation) and Einstein (photoelectric effect), physicists understood that electromagnetic waves sometimes behaved like particles. De Broglie’s hypothesis is complementary to this idea: particles should also show wave-like properties such as diffraction or interference. De Broglie’s formula was confirmed three years later for electrons (which have a rest-mass) with the observation of electron diffraction in two independent experiments. George Paget Thomson passed a beam of electrons through a thin metal film and observed the predicted interference patterns. Clinton Joseph Davisson and Lester Halbert Germerguided their beam through a crystalline grid to observe diffraction patterns.
X-ray diffraction is a commonly used tool in materials research. Thanks to the wave-particle duality, matter wave diffraction can also be used for this purpose. The electron, which is easy to produce and manipulate, is a common choice. A neutron is another particle of choice. Due to the different kinds of interactions involved in the diffraction processes, the three types of radiation (X-ray, electron, neutron) are suitable for different kinds of studies.
Electron diffraction is most frequently used in solid state physics and chemistry to study the crystalline structure of solids. Experiments are usually performed using a transmission electron microscope or a scanning electron microscope. In these instruments, electrons are accelerated by an electrostatic potential in order to gain the desired energy and, thus, wavelength before they interact with the sample to be studied. The periodic structure of a crystalline solid acts as a diffraction grating, scattering the electrons in a predictable manner. Working back from the observed diffraction pattern, it is then possible to deduce the structure of the crystal producing the diffraction pattern. Unlike other types of radiation used in diffraction studies of materials, such as X-rays and neutrons, electrons are charged particles and interact with matter through the Coulomb forces. This means that the incident electrons feel the influence of both the positively charged atomic nuclei and the surrounding electrons. In comparison, X-rays interact with the spatial distribution of the valence electrons, while neutrons are scattered by the atomic nuclei through the strong nuclear force.

Electron Diffraction Pattern: Typical electron diffraction pattern obtained in a transmission electron microscope with a parallel electron beam.
Neutrons have also been used for studying crystalline structures. They are scattered by the nuclei of the atoms, unlike X-rays, which are scattered by the electrons of the atoms. Thus, neutron diffraction has some key differences compared to more common methods using X-rays or electrons. For example, the scattering of X-rays is highly dependent on the atomic number of the atoms (i.e., the number of electrons), whereas neutron scattering depends on the properties of the nuclei. In addition, the magnetic moment of the neutron is non-zero, and can thus also be scattered by magnetic fields. This means that neutron scattering is more useful for determining the properties of atomic nuclei, despite the fact that neutrons are significantly harder to create, manipulate, and detect compared to X-rays and electrons.
The Wave Function
A wave function is a probability amplitude in quantum mechanics that describes the quantum state of a particle and how it behaves.
learning objectives
- Relate the wave function with the probability density of finding a particle, commenting on the constraints the wave function must satisfy for this to make sense
In quantum mechanics, a wave function is a probability amplitude describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers. For a single particle, it is a function of space and time. The most common symbols for a wave function are \(\psi ( x )\) or \(\Psi ( x )\) (lowercase or uppercase psi, respectively), when the wave function is given as a function of position \(\mathrm{x}\). Although \(\psi\) is a complex number, \(| \psi | 2\) is a real number and corresponds to the probability density of finding a particle in a given place at a given time, if the particle’s position is measured.
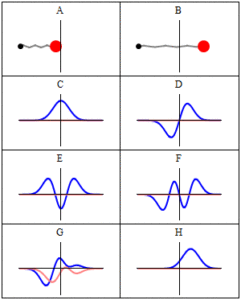
Trajectories of a Harmonic Oscillator: This figure shows some trajectories of a harmonic oscillator (a ball attached to a spring) in classical mechanics (A-B) and quantum mechanics (C-H). In quantum mechanics (C-H), the ball has a wave function, which is shown with its real part in blue and its imaginary part in red. The trajectories C-F are examples of standing waves, or “stationary states. ” Each standing-wave frequency is proportional to a possible energy level of the oscillator. This “energy quantization” does not occur in classical physics, where the oscillator can have any energy.
The laws of quantum mechanics (the Schrödinger equation) describe how the wave function evolves over time. The wave function behaves qualitatively like other waves, such as water waves or waves on a string, because the Schrödinger equation is mathematically a type of wave equation. This explains the name “wave function” and gives rise to wave-particle duality.
The wave function must satisfy the following constraints for the calculations and physical interpretation to make sense:
- It must everywhere be finite.
- It must everywhere be a continuous function and continuously differentiable.
- It must everywhere satisfy the relevant normalization condition so that the particle (or system of particles) exists somewhere with 100-percent certainty.
If these requirements are not met, it’s not possible to interpret the wave function as a probability amplitude. This is because the values of the wave function and its first order derivatives may not be finite and definite (having exactly one value), which means that the probabilities can be infinite and have multiple values at any one position and time, which is nonsense. Furthermore, when we use the wave function to calculate an observation of the quantum system without meeting these requirements, there will not be finite or definite values to use (in this case the observation can take a number of values and can be infinite). This is not a possible occurrence in a real-world experiment. Therefore, a wave function is meaningful only if these conditions are satisfied.
de Broglie and the Wave Nature of Matter
The concept of “matter waves” or “de Broglie waves” reflects the wave-particle duality of matter.
learning objectives
- Formulate the de Broglie relation as an equation
In quantum mechanics, the concept of matter waves (or de Broglie waves) reflects the wave-particle duality of matter. The theory was proposed by Louis de Broglie in 1924 in his PhD thesis. The de Broglie relations show that the wavelength is inversely proportional to the momentum of a particle, and is also called de Broglie wavelength.
Einstein derived in his theory of special relativity that the energy and momentum of a photon has the following relationship:
\(\mathrm { E } = \mathrm { p } \mathrm { c }\) (\(\mathrm{E}\): energy, \(\mathrm{p}\): momentum, \(\mathrm{c}\): speed of light).
He also demonstrated, in his study of photoelectric effects, that energy of a photon is directly proportional to its frequency, giving us this equation:
\(\mathrm { E } = \mathrm { h} \nu \) (\(\mathrm{h}\): Planck constant, \(\nu\): frequency).
Combining the two equations, we can derive a relationship between the momentum and wavelength of light:
\(\mathrm { p } = \frac { \mathrm { E } } { \mathrm { c } } = \frac { \mathrm { h } \nu } { \mathrm { c } } = \frac { \mathrm { h } } { \lambda }\). Therefore, we arrive at \(\mathrm{\lambda = \frac { h } { p }}\).
De Broglie’s hypothesis is that this relationship \(\mathrm{λ=hp}\), derived for electromagnetic waves, can be adopted to describe matter (e.g. electron, neutron, etc.) as well.
De Broglie didn’t have any experimental proof at the time of his proposal. It took three years for Clinton Davisson and Lester Germer to observe diffraction patterns from electrons passing a crystalline metallic target (see ). Before the acceptance of the de Broglie hypothesis, diffraction was a property thought to be exhibited by waves only. Therefore, the presence of any diffraction effects by matter demonstrated the wave-like nature of matter. This was a pivotal result in the development of quantum mechanics. Just as the photoelectric effect demonstrated the particle nature of light, the Davisson–Germer experiment showed the wave-nature of matter, thus completing the theory of wave-particle duality.
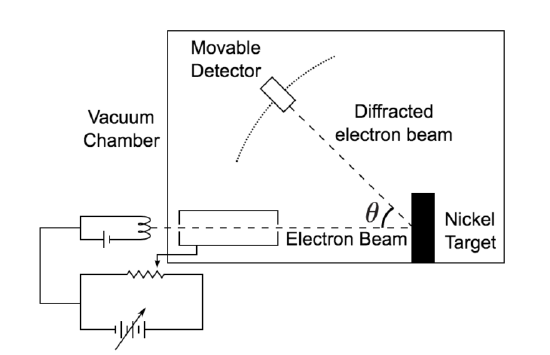
Davisson-Germer Experimental Setup: The experiment included an electron gun consisting of a heated filament that released thermally excited electrons, which were then accelerated through a potential difference (giving them a certain amount of kinetic energy towards the nickel crystal). To avoid collisions of the electrons with other molecules on their way towards the surface, the experiment was conducted in a vacuum chamber. To measure the number of electrons that were scattered at different angles, an electron detector that could be moved on an arc path about the crystal was used. The detector was designed to accept only elastically scattered electrons.
Experiments with Fresnel diffraction and specular reflection of neutral atoms confirm the application to atoms of the de Broglie hypothesis. Further, recent experiments confirm the relations for molecules and even macromolecules, normally considered too large to undergo quantum mechanical effects. In 1999, a research team in Vienna demonstrated diffraction for molecules as large as fullerenes. The researchers calculated a De Broglie wavelength of the most probable \(\mathrm{C_{60}}\) velocity as 2.5 pm.
The Heisenberg Uncertainty Principle
The uncertainty principle asserts a basic limit to the precision with which some physical properties of a particle can be known simultaneously.
learning objectives
- Relate the Heisenberg uncertainty principle with the matter wave nature of all quantum objects
The uncertainty principle is any of a variety of mathematical inequalities, asserting a fundamental limit to the precision with which certain pairs of physical properties of a particle, such as position \(\mathrm{x}\) and momentum pp or energy \(\mathrm{E}\) and time \(\mathrm{t}\), can be known simultaneously. The more precisely the position of some particle is determined, the less precisely its momentum can be known, and vice versa. This can be formulated as the following inequality: \(\sigma _ { \mathrm { x } } \sigma _ { \mathrm { y } } \geq \frac { \mathrm { \overline{h} } } { 2 }\), where \(\mathrm{σ_x}\) is the standard deviation of position, σp is the standard deviation of momentum, and \(\overline { \mathrm { h } } = \frac { \mathrm { h } } { 2 \pi }\). The uncertainty principle is inherent in the properties of all wave-like systems, and it arises in quantum mechanics simply due to the matter wave nature of all quantum objects. Thus, the uncertainty principle actually states a fundamental property of quantum systems, and is not a statement about the observational success of current technology.
The principle is quite counterintuitive, so the early students of quantum theory had to be reassured that naive measurements to violate it were bound always to be unworkable. One way in which Heisenberg originally illustrated the intrinsic impossibility of violating the uncertainty principle is by using an imaginary microscope as a measuring device.
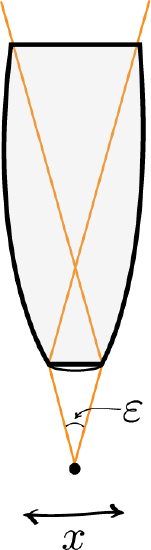
Heisenberg Microscope: Heisenberg’s microscope, with cone of light rays focusing on a particle with angle \(ϵ\) He imagines an experimenter trying to measure the position and momentum of an electron by shooting a photon at it.
Example \(\PageIndex{1}\):
Example One
If the photon has a short wavelength and therefore a large momentum, the position can be measured accurately. But the photon scatters in a random direction, transferring a large and uncertain amount of momentum to the electron. If the photon has a long wavelength and low momentum, the collision does not disturb the electron’s momentum very much, but the scattering will reveal its position only vaguely.
Example Two
If a large aperture is used for the microscope, the electron’s location can be well resolved (see Rayleigh criterion); but by the principle of conservation of momentum, the transverse momentum of the incoming photon and hence the new momentum of the electron resolves poorly. If a small aperture is used, the accuracy of both resolutions is the other way around.
Heisenberg’s Argument
Heisenberg’s argument is summarized as follows. He begins by supposing that an electron is like a classical particle, moving in the xx direction along a line below the microscope, as in the illustration to the right. Let the cone of light rays leaving the microscope lens and focusing on the electron makes an angle εε with the electron. Let \(\lambda\) be the wavelength of the light rays. Then, according to the laws of classical optics, the microscope can only resolve the position of the electron up to an accuracy of \(\delta \mathrm { x } = \frac { \lambda } { \sin ( \varepsilon / 2 ) }\) When an observer perceives an image of the particle, it’s because the light rays strike the particle and bounce back through the microscope to their eye. However, we know from experimental evidence that when a photon strikes an electron, the latter has a recoil with momentum proportional to \(\mathrm{h/λ}\), where \(\mathrm{h}\) is Planck’s constant.
It is at this point that Heisenberg introduces objective indeterminacy into the thought experiment. He writes that “the recoil cannot be exactly known, since the direction of the scattered photon is undetermined within the bundle of rays entering the microscope”. In particular, the electron’s momentum in the xx direction is only determined up to δpx≈hλsin(ε/2)δpx≈hλsin(ε/2). Combining the relations for \(\mathrm{δx}\) and \(\mathrm{δp_x}\), we thus have that \(\delta \mathbf { x } \cdot \delta \mathrm { p } _ { \mathbf { x } } \approx \left( \frac { \lambda } { \sin ( \varepsilon / 2 ) } \right) \left( \frac { \mathrm { h } } { \lambda } \sin ( \varepsilon / 2 ) \right) = \mathrm { h }\), which is an approximate expression of Heisenberg’s uncertainty principle.
Heisenberg Uncertainty Principle Derived and Explained
One of the most-oft quoted results of quantum physics, this doozie forces us to reconsider what we can know about the universe. Some things cannot be known simultaneously. In fact, if anything about a system is known perfectly, there is likely another characteristic that is completely shrouded in uncertainty. So significant figures ARE important after all!
Philosophical Implications
Since its inception, many counter-intuitive aspects of quantum mechanics have provoked strong philosophical debates.
learning objectives
- Formulate the Copenhagen interpretation of the probabilistic nature of quantum mechanics
Since its inception, many counter-intuitive aspects and results of quantum mechanics have provoked strong philosophical debates and many interpretations. Even fundamental issues, such as Max Born’s basic rules interpreting \(ψ∗ψ\) as a probability density function took decades to be appreciated by society and many leading scientists. Indeed, the renowned physicist Richard Feynman once said, “I think I can safely say that nobody understands quantum mechanics. ”
The Copenhagen Interpretation
The Copenhagen interpretation—due largely to the Danish theoretical physicist Niels Bohr, shown in —remains a quantum mechanical formalism that is widely accepted amongst physicists, some 75 years after its enunciation. According to this interpretation, the probabilistic nature of quantum mechanics is not a temporary feature which will eventually be replaced by a deterministic theory, but instead must be considered a final renunciation of the classical idea of causality.

Niels Bohr and Albert Einstein: Niels Bohr (left) and Albert Einstein (right). Despite their pioneering contributions to the inception of the quantum mechanics, they disagreed on its interpretation.
The Copenhagen interpretation has philosophical implications to the concept of determinism. According to the theory of determinism, for everything that happens there are conditions such that, given those conditions, nothing else could happen. Determinism and free-will seem to be mutually exclusive. If the universe, and any person in it are governed by strict and universal laws , then that means that a person’s behavior could be predicted based on sufficient knowledge of the circumstances obtained prior to that person’s behavior. However, the Copenhagen interpretation suggests a universe in which outcomes are not fully determined by prior circumstances but also by probability. This gave thinkers alternatives to strictly bound possibilities, proposing a model for a universe that follows general rules but never had a predetermined future.
Philosophical Implications
It is also believed therein that any well-defined application of the quantum mechanical formalism must always make reference to the experimental arrangement. This is due to the quantum mechanical principle of wave function collapse. That is, a wave function which is initially in a superposition of several different possible states appears to reduce to a single one of those states after interaction with an observer. In simplified terms, it is the reduction of the physical possibilities into a single possibility as seen by an observer. This raises philosophical questions about whether something that is never observed actually exists.
Einstein-Podolsky-Rosen (EPR) Paradox
Albert Einstein (shown in , himself one of the founders of quantum theory) disliked this loss of determinism in measurement in the Copenhagen interpretation. Einstein held that there should be a local hidden variable theory underlying quantum mechanics and, consequently, that the present theory was incomplete. He produced a series of objections to the theory, the most famous of which has become known as the Einstein-Podolsky-Rosen (EPR) paradox. John Bell showed by Bell’s theorem that this “EPR” paradox led to experimentally testable differences between quantum mechanics and local realistic theories. Experiments have been performed confirming the accuracy of quantum mechanics, thereby demonstrating that the physical world cannot be described by any local realistic theory. The Bohr-Einstein debates provide a vibrant critique of the Copenhagen Interpretation from an epistemological point of view.
Quantum Entanglement
One of the most bizarre aspect of the quantum mechanics is known as quantum entanglement. Quantum entanglement occurs when particles interact physically and then become separated, while isloated from the rest of the universe to prevent any deterioration of the quantum state. According to the Copenhagen interpretation of quantum mechanics, their shared state is indefinite until measured. Once a particle in the entangled state is measured and its state is determined, the Copenhagen interpretation demands that the other particles’ state is also determined instantaneously. This bizarre nature of action at a distance (which seemingly violate the speed limit on the transmission of information implicit in the theory of relativity) is what bothered Einstein the most. (According to the theory of relativity, nothing can travel faster than the speed of light in a vacuum. This seemingly puts a limit on the speed at which information can be transmitted. ) Quantum entanglement is the key element in proposals for quantum computers and quantum teleportation.
Key Points
- The energy of the emitted electrons depends only on the frequency of the incident light, and not on the light intensity.
- Einstein explained the photoelectric effect by describing light as composed of discrete particles.
- Study of the photoelectric effect led to important steps in understanding the quantum nature of light and electrons, which would eventually lead to the concept of wave-particle duality.
- Electromagnetic radiation is classified according to wavelength, divided into radio waves, microwaves, terahertz (or sub-millimeter) radiation, infrared, the visible region humans perceive as light, ultraviolet, X-rays, and gamma rays.
- Photon energy is proportional to the frequency of the radiation.
- Most parts of the electromagnetic spectrum are used in science for spectroscopic and other probing interactions as ways to study and characterize matter.
- \(\mathrm { E } = \mathrm { hv }\) Energy of photon is proportional to its frequency.
- \(\mathrm{p=hk}\) Momentum of photon is proportional to the wave vector.
- Photon’s rest mass is 0.
- A great number of modern technological inventions are based on quantum mechanics, including the laser, the transistor, the electron microscope, and magnetic resonance imaging.
- Quantum mechanics is also critically important for understanding how individual atoms combine covalently to form molecules. The application of quantum mechanics to chemistry is known as quantum chemistry.
- Researchers are currently seeking robust methods of directly manipulating quantum states for applications in computer and information science.
- All entities in Nature behave as both a particle and a wave, depending on the specifics of the phenomena under consideration.
- Particle-wave duality is usually hidden in macroscopic phenomena, conforming to our intuition.
- In the double-slit experiment of electrons, individual event displays a particle-like property of localization (or a “dot”). After many repetitions, however, the image shows an interference pattern, which indicates that each event is in fact governed by a probability distribution.
- The wavelength of an electron is given by the de Broglie equation \(\mathrm{\lambda = \frac { h } { p }}\).
- Because of different forms of interaction involved, X-ray, electron, and neutron are suitable for different studies of material properties.
- De Broglie’s idea completed the wave-particle duality.
- \(| \psi | 2 ( \mathrm { x } )\) corresponds to the probability density of finding a particle in a given location x at a given time.
- The laws of quantum mechanics (the Schrödinger equation) describe how the wave function evolves over time. The Schrödinger equation is a type of wave equation, which explains the name “wave function”.
- A wave function must satisfy a set of mathematical constraints for the calculations and physical interpretation to make sense.
- de Broglie relations show that the wavelength is inversely proportional to the momentum of a particle.
- The Davisson-Germer experiment demonstrated the wave-nature of matter and completed the theory of wave-particle duality.
- Experiments demonstrated that de Broglie hypothesis is applicable to atoms and macromolecules.
- The uncertainty principle is inherent in the properties of all wave-like systems, and that it arises in quantum mechanics is simply due to the matter wave nature of all quantum objects.
- The uncertainty principle is not a statement about the observational success of current technology.
- The more precisely the position of some particle is determined, the less precisely its momentum can be known, and vice versa. This can be formulated as the following inequality: \(\sigma _ { \mathrm { X } } \sigma _ { \mathrm { y } } \geq \frac { \mathrm { \overline{h} } } { 2 }\).
- According to the Copenhagen interpretation, the probabilistic nature of quantum mechanics is intrinsic in our physical universe.
- When quantum wave function collapse occurs, physical possibilities are reduced into a single possibility as seen by an observer.
- Once a particle in an entangled state is measured and its state is determined, the Copenhagen interpretation demands that the state of the other entangled particle is also determined instantaneously.
Key Terms
- black body radiation: The type of electromagnetic radiation within or surrounding a body in thermodynamic equilibrium with its environment, or emitted by a black body (an opaque and non-reflective body) held at constant, uniform temperature.
- photoelectron: Electrons emitted from matter by absorbing energy from electromagnetic radiation.
- wave-particle duality: A postulation that all particles exhibit both wave and particle properties. It is a central concept of quantum mechanics.
- Planck constant: a physical constant that is the quantum of action in quantum mechanics. It has a unit of angular momentum. The Planck constant was first described as the proportionality constant between the energy of a photon (unit of electromagnetic radiation) and the frequency of its associated electromagnetic wave in his derivation of the Planck’s law
- Maxwell’s equations: A set of equations describing how electric and magnetic fields are generated and altered by each other and by charges and currents.
- elementary particle: a particle not known to have any substructure
- photoelectric effect: The occurrence of electrons being emitted from matter (metals and non-metallic solids, liquids, or gases) as a consequence of their absorption of energy from electromagnetic radiation.
- cryptography: the practice and study of techniques for secure communication in the presence of third parties
- relativistic quantum mechanics: a theoretical framework for constructing quantum mechanical models of fields and many-body systems
- string theory: an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity
- black body: An idealized physical body that absorbs all incident electromagnetic radiation, regardless of frequency or angle of incidence. Although black body is a theoretical concept, you can find approximate realizations of black body in nature.
- grating: Any regularly spaced collection of essentially identical, parallel, elongated elements.
- Schrödinger equation: A partial-differential that describes how the quantum state of some physical system changes with time. It was formulated in late 1925 and published in 1926 by the Austrian physicist Erwin Schrödinger
- harmonic oscillator: a system that, when displaced from its equilibrium position, experiences a restoring force \(\mathbf{F}\) proportional to the displacement x
- diffraction: The bending of a wave around the edges of an opening or an obstacle.
- special relativity: A theory that (neglecting the effects of gravity) reconciles the principle of relativity with the observation that the speed of light is constant in all frames of reference.
- wave-particle duality: A postulation that all particles exhibit both wave and particle properties. It is a central concept of quantum mechanics.
- matter wave: A concept reflects the wave-particle duality of matter. The theory was proposed by Louis de Broglie.
- Rayleigh criterion: The angular resolution of an optical system can be estimated from the diameter of the aperture and the wavelength of the light, which was first proposed by Lord Rayleigh.
- probability density function: Any function whose integral over a set gives the probability that a random variable has a value in that set.
- Bell’s theorem: A no-go theorem famous for drawing an important line in the sand between quantum mechanics (QM) and the world as we know it classically. In its simplest form, Bell’s theorem states: No physical theory of local hidden variables can ever reproduce all of the predictions of quantum mechanics.
- epistemological: Of or pertaining to epistemology or theory of knowledge, as a field of study.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- photoelectron. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/photoelectron. License: CC BY-SA: Attribution-ShareAlike
- black body radiation. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/black%20body%20radiation. License: CC BY-SA: Attribution-ShareAlike
- photoelectric effect. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Photoelectric_effect. License: CC BY-SA: Attribution-ShareAlike
- Photoelectric effect.svg. Provided by: Wikipedia. Located at: en.Wikipedia.org/w/index.php?title=File:Photoelectric_effect.svg&page=1. License: CC BY-SA: Attribution-ShareAlike
- Electromagnetic spectrum. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Electromagnetic_spectrum. License: CC BY-SA: Attribution-ShareAlike
- Maxwell's equations. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Maxwellu2019s%20equations. License: CC BY-SA: Attribution-ShareAlike
- Planck constant. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Planck%20constant. License: CC BY-SA: Attribution-ShareAlike
- elementary particle. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/elementary%20particle. License: CC BY-SA: Attribution-ShareAlike
- Photon. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Photon. License: CC BY-SA: Attribution-ShareAlike
- black body radiation. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/black%20body%20radiation. License: CC BY-SA: Attribution-ShareAlike
- Military laser experiment.jpg. Provided by: Wikimedia. Located at: http://upload.wikimedia.org/Wikipedia/commons/a/a0/Military_laser_experiment.jpg. License: CC BY: Attribution
- string theory. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/string%20theory. License: CC BY-SA: Attribution-ShareAlike
- cryptography. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/cryptography. License: CC BY-SA: Attribution-ShareAlike
- Quantum mechanics. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Quantum_mechanics%23Applications. License: CC BY-SA: Attribution-ShareAlike
- relativistic quantum mechanics. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/relativistic%20quantum%20mechanics. License: CC BY-SA: Attribution-ShareAlike
- Laser. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Laser. License: CC BY: Attribution
- Particle wave. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Particle_wave. License: CC BY-SA: Attribution-ShareAlike
- Copenhagen interpretation. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Copenhagen_interpretation. License: CC BY-SA: Attribution-ShareAlike
- photoelectric effects. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/photoelectric%20effects. License: CC BY-SA: Attribution-ShareAlike
- Electric diffraction. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Electron_diffraction. License: CC BY-SA: Attribution-ShareAlike
- grating. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/grating. License: CC BY-SA: Attribution-ShareAlike
- Electric diffraction. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Electron_diffraction. License: CC BY-SA: Attribution-ShareAlike
- Gabriela Escalera, Andrew Barron, Neutron Diffraction. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m43582/latest/. License: CC BY: Attribution
- Schrodinger equation. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Schrodinger%20equation. License: CC BY-SA: Attribution-ShareAlike
- harmonic oscillator. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/harmonic%20oscillator. License: CC BY-SA: Attribution-ShareAlike
- Wave function. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Wave_function%23Requirements. License: CC BY-SA: Attribution-ShareAlike
- wave-particle duality. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/wave-particle%20duality. License: CC BY-SA: Attribution-ShareAlike
- De Broglie wavelength. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/De_Broglie_wavelength. License: CC BY-SA: Attribution-ShareAlike
- special relatively. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/special_relativity. License: CC BY-SA: Attribution-ShareAlike
- diffraction. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/diffraction. License: CC BY-SA: Attribution-ShareAlike
- Uncertainty principle. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Uncertainty_principle. License: CC BY-SA: Attribution-ShareAlike
- Rayleigh criterion. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Rayleigh%20criterion. License: CC BY-SA: Attribution-ShareAlike
- Heisenberg's microscope. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Heisenbergu2019s_microscope. License: CC BY-SA: Attribution-ShareAlike
- matter wave. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/matter%20wave. License: CC BY-SA: Attribution-ShareAlike
- Heisenberg's microscope. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Heisenbergu2019s_microscope. License: CC BY: Attribution
- Bell's theorem. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Bellu2019s%20theorem. License: CC BY-SA: Attribution-ShareAlike
- probability density function. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/probability_density_function. License: CC BY-SA: Attribution-ShareAlike
- epistemological. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/epistemological. License: CC BY-SA: Attribution-ShareAlike
- Bohr–Einstein debates. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Bohr%E2%80%93Einstein_debates. License: CC BY: Attribution

