7.2: Monte Carlo for Biomembranes
- Page ID
- 1981
Complexity of Biological Membranes
The fluid mosaic model proposed by Jonathan Singer and Garth Nicolson in 1972 served as the starting point for our modern understanding of biological membranes [1]. A visual example of their model is depicted in Figure \(\PageIndex{1}\). Their model describes the biological membrane bilayer as an integration of proteins and lipids – capable of communicating and interacting to serve the necessary functions of the cell. These interactions can control movement of material in and out of the cell through protein pores, form lipid rafts, and regulate vesicle formation. This article will focus on computational methods used to study biomembranes (specifically Monte Carlo) but will start by examining the need of such tools.

Different Approaches: Experiments and Computation
Various experimental techniques have helped unravel numerous complexities of biomembranes. These include lipid photolabeling, X-ray crystallography, and NMR; each with distinguishing limitations and information provided [1,2]. Not only has our understanding of biomembranes been enhanced by experimental techniques, but structure-function characterization of membrane proteins has also provided targets for successful medical applications [1].
However, despite the success of these techniques, some biomembrane studies are currently too complex for experiments. Spectroscopic and structural analysis of lipid aggregates, for instance, average over several aggregate conformations and are unable to provide information on individual conformations [3]. Non-lamellar bilayer phases, which are associated with transient membrane heterogeneic states, are also difficult to study using experimental techniques [3].
Computational tools can facilitate these studies, and have deepened our knowledge of biomembranes in conjunction with experiments. For example, molecular dynamics and Monte Carlo simulations – along with various microscopy studies – have enhanced our understanding of lipid nanodomains and their role in membrane raft formation [3-6].
Computational Methods in Biomembranes: Introduction
Though several computational methods have been developed to examine biomembrane dynamics, two widely utilized methods are molecular dynamics (MD) and Monte Carlo (MC) simulations. MD involves numerical integration of macromolecular trajectories based on Newton’s equations and describes the development of macromolecular position, orientation, and force fields through time [3-5,7-9].
While MD is relatively straightforward and highly detailed, it is restricted by short simulation times (~fs - µs) and cannot account for slower (~ms) membrane dynamics – such as lipid flip-flops and lipid domain formation – due to short integration time-steps (~fs) [2,5,7,9]. MC can bypass this time-dependence and potentially provide similar results to MD [2]. MC relies on sampling and generating likely configurations of the system based on thermodynamic conditions and applied perturbations [6-8]. However, MC has its own limitations: it contains biased configuration transitions, and some algorithms are more complicated and niche than MD [7]. Though both approaches study biomembranes in distinct ways, they are not mutually exclusive; MD and MC approaches have been combined to enrich bilayer equilibration studies [2].
Monte Carlo – Basic Principles
Diverse MC variations have been developed to address wide-ranging questions related to biomembranes: an algorithm exploring diffusion in two-component membranes incorporated calculations involving the Hamiltonian and Gibbs free energy, while another study focusing on enzyme reactions in 2D lattices incorporated Michaelis-Menten kinetics [10,11]. Nevertheless, many MC methods share similar properties.
Essentially, MC schemes involve modeling the selected system with a set of probability density functions (PDFs), and repeatedly sampling these functions to generate potential outcomes of the system [12]. Depending on the output desired the details of the model will vary. In the case of biomembranes, thermodynamics governs these probability functions [8].
Lagrangian and Hamiltonian dynamics control the evolution of macromolecular systems in MC, as well as MD [8]. The Lagrangian is the difference between the kinetic and potential energy, and the Hamiltonian, defined in Equation \ref{1}, is the Legendre transformation of the Lagrangian:
\[\mathscr{H}\left(q^{3 N}, p^{3 N}\right)=\sum_{\alpha=1}^{3 N} p^{\alpha} q_{\alpha}-\mathscr{L}\left(q^{3 N}, \dot{q}^{3 N}\left(q^{3 N}, p^{3 N}\right)\right) \label{1}\]
Equation 1: The Hamiltonian [8].
where q3N are the generalized coordinates, p3N are the generalized momenta, and q̇3N are the generalized velocities. The partition function, which describes various probabilities of different states of the system, is given in Equation \ref{2} as:
\[Z(N, V, T) \equiv \int d \mathbf{p}^{N} d \mathbf{r}^{N} \exp \left[-\beta \mathscr{H}\left(\mathbf{r}^{N}, \mathbf{p}^{N}\right)\right] \label{2}\]
Equation 2: The partition function [8].
where rN represents the Cartesian coordinates of the system and β is the thermodynamic beta. The probability that a macromolecule is in a particular state with positions rN and momenta pN is given by Equation \ref{3}:
\[\operatorname{Pr}\left(\mathbf{r}^{N}, \mathbf{p}^{N}\right) d \mathbf{p}^{N} d \mathbf{r}^{N}=\frac{\exp \left[-\beta \mathscr{H}\left(\mathbf{r}^{N}, \mathbf{p}^{N}\right)\right] d \mathbf{p}^{N} d \mathbf{r}^{N}}{Z(N, V, E)} \label{3}\]
Equation 3: Probability function that describes the probability of a molecule with a specific energy [8].
and the observed average state of the system (enthalpy, entropy, etc.) can be calculated by summing the values of the state and their associated probabilities, given by Equation \ref{4}:
\[\langle O\rangle=\int d \mathbf{p}^{N} d \mathbf{r}^{N} O\left(\mathbf{r}^{N}, \mathbf{p}^{N}\right) \operatorname{Pr}\left(\mathbf{r}^{N}, \mathbf{p}^{N}\right) \label{4}\]
Equation 4. The system average observable O [8].
Generating representative states of the system requires Markov chain sampling of the configuration space, numerically integrating probability functions, and calculating the observed average state [8]. An MC bilayer simulation example is provided in Figure 2. Transitions between states in a sample depends on energy. In Metropolis MC, transitions to a lower energy state is accepted each time, while transitions to a higher energy state are accepted with a certain probability [8].
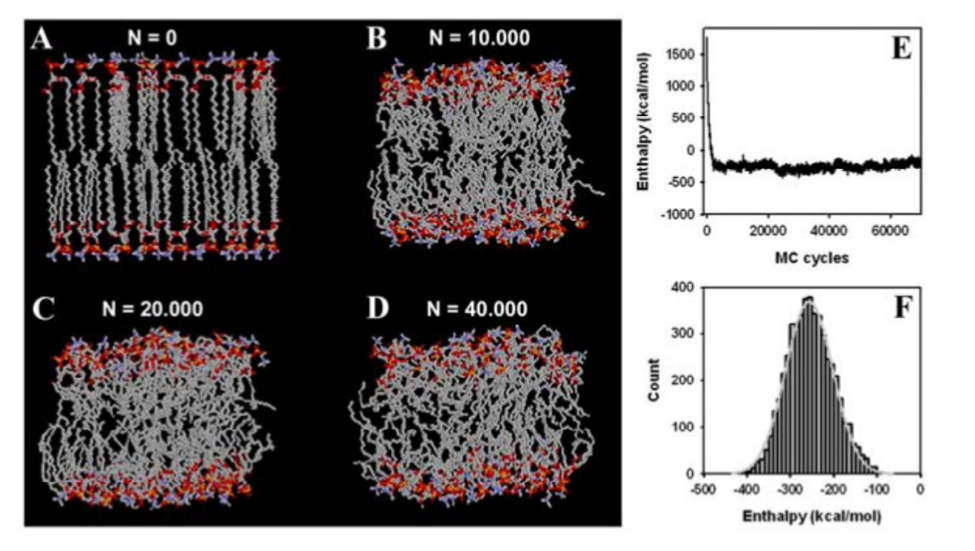
Issues to Consider
While MC can be useful to study populations of biomembrane configuration states, there are some issues to consider. It is extremely difficult to generate independent distributions for each biomolecule (or other entity) in the system due to computational limitations; MC sampling can also miss rare configuration spaces depending on the sampling size [13]. Defining adequate sampling will depend on the system of interest and available computational resources.
In addition, initial conditions of the model can influence MC sampling [11]. In the case of protein folding, initial conditions near the unfolded state can extend adequate sampling time to unreasonable lengths [13]. This is due to the vast configuration space surrounding the folded state(s). Understanding and controlling model sensitivity to initial conditions can help optimize MC sampling.
Level of Detail – Atomistic to Coarse Grained Models
While there are several levels of biomembrane modeling, this article will briefly discuss only atomistic and coarse-grained models.
Atomistic models describe atoms – bond angles, torsion angles, electrostatic and van der Waals interactions – and how these physical properties underlie complex lipid structure [9]. Coarse-graining on the other hand (Figure 3), examines collective behavior (of atoms, etc.) and how they contribute to collective membrane phenomena (phase transitions, vesicle fusion) [2-5,9].
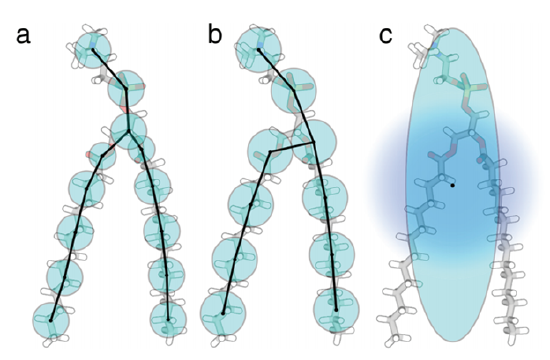
The choice of detail will depend on the study and the available resources. While atomistic models provide highly detailed analyses, they require large amounts of computing power and are restricted to timescales of picoseconds to microseconds [2,3,5,9]. Coarse-grained models sacrifice some detail but significantly speed computational time due to reduced degrees of freedom, and they can examine behavior above the microsecond timescale [2-5,9].
MC Applications for Biomembranes
MC has been utilized for numerous biomembrane studies. These studies include:
- Characterizing protein-membrane interactions:
- Cooperation between G-protein coupled receptors and lipid rafts [15].
- Annexin-mediated domain formation with cholesterol [16].
- Structure and dynamics of biomembranes:
- Vesicle structure under different nematogen concentrations [17].
- Phase separation and formation of nanodomains.
- Membrane structure under varying cholesterol and protein compositions.
These represent some of the numerous applications of MC to biomembranes.
Summary
- Computational tools – in conjunction with experiments – can significantly strengthen our knowledge of biomembranes.
- MC is one of the computational tools we can use, and extracts information about potential configurations in biomembranes.
- There are numerous issues to consider when using computational tools, which will depend on the study and the available resources.
References
- Xia, Y. and Peng, L. 2013. Photoactivatable Lipid Probes for Studying Biomembranes by Photoaffinity Labeling. Chem Rev. 113: 7880-7929.
- Wüstner, D. and Skelenar, H. 2014. Atomistic Monte Carlo Simulation of Lipid Membranes. Int J Mol Sci. 15: 1767-1803.
- Marrink, S.J. et al. 2009. Lipids on the move: Simulations of membrane pores, domains, stalks and curves. Biochim Biophys Acta. 1788: 149-168.
- Elson, E.L. et al. 2010. Phase separation in biological membranes: integration of theory and experiment. Annu Rev Biophys. 39: 207-226.
- Rouse, S. et al. 2010. Molecular Simulations and Biomembranes: From Biophysics to Function. First Edition. Cambridge CB4 0WF, UK: The Royal Society of Chemistry.
- Heimburg, T. 2000. Monte Carlo simulations of lipid bilayers and lipid protein interactions in the light of recent experiments. Curr Opin Colloid Interface Sci. 5: 224-231.
- Pastor, R.W. 1994. Molecular dynamics and Monte Carlo simulations of lipid bilayers. Curr Opin Struct Biol. 4: 486-492.
- Paquet, E. and Viktor, H.L. 2015. Molecular Dynamics, Monte Carlo Simulations, and Langevin Dynamics: A Computational Review. BioMed Res Int. vol. 2015, Article ID 183918, 18 pages. doi:10.1155/2015/183918.
- Müeller, M. et al. 2006. Biological and synthetic membranes: What can be learned from a coarse-grained description? Phys Rep. 434: 113-176.
- Hac, A.E. et al. 2005. Diffusion in Two-Component Lipid Membranes – A Fluorescence Correlation Spectroscopy and Monte Carlo Simulation Study. Biophys J. 88: 317-333.
- Berry, H. 2002. Monte carlo simulations of enzyme reactions in two dimensions: fractal kinetics and spatial segregation. Biophys J. 83: 1891-1901.
- Harrison, R.L. 2010. Introduction To Monte Carlo Simulation. AIP Conf Proc. 1204: 17-21.
- Zuckerman, D.M. 2011. Equilibrium Sampling in Biomolecular Simulations. Annu Rev Biophys. 40: 41-62.
- Ingólfsson, H.I. et al. 2014. The power of coarse graining in biomolecular simulations. Wiley Interdiscip Rev Comput Mol Sci. 4: 225-248.
- Fallahi-Sichani, M. and Linderman, J.J. 2009. Lipid Raft-Mediated Regulation of G-Protein Coupled Receptor Signaling by Ligands which Influence Receptor Dimerization: A Computational Study. PLoS One. 4: e6604.
- Almeida, P.F. et al. 2011. Monte Carlo Simulation of Protein-Induced Lipid Demixing in a Membrane with Interactions Derived from Experiment. Biophys J. 101: 1930-1937.
- Sreeja, K.K. et al. 2015. Monte Carlo simulations of fluid vesicles. J Phys Condens Matter. 27:273104. doi: 10.1088/0953-8984/27/27/273104.

