6.3: Electrospray Ionization (ESI) Mass Spectrometry
- Page ID
- 14603
Electrospray Ionization Mass Spectrometry is a technique used to determine molecular weights for proteins, peptides, and other biological macromolecules such as oligosaccharides1. Originally described by Canadian-American Physicist Sir Arthur J. Dempster in an article titled "A new method of positive ray analysis."7 His work was the first modern mass spectrometer, which used positive rays to determine the mass-to-charge ratio of various isotopes of lithium and magnesium. Dempster showed that it was possible to determine the isotopes' relative proportions and atomic weights using this method7. Mass spectrometry in general is useful for structure elucidation (when combined with chromatography separation techniques), peptide sequencing (when combined with ion traps), and quantification (when combined with a triple-quadrupole mass analyzer) for example, and is mainly limited by the ability of the ions generated to remain stable until their arrival at the detector. Electrospray Ionization describes the method by which the macromolecules are ionized via a “soft” ionization, which does not fragment nor harshly degrade the macromolecules and ionizes by multiple charging1. Rather, the macromolecules are ionized into small droplets2. The droplets are then desolvated further, effectively decreasing the droplet size into molecules with protons1. The protonated/desolvated molecules enter the mass analyzer and subsequently the detector to determine the mass/charge ratio1. The main advantage is that the samples can easily be introduced to the instrument in solution with the ability to detect very small masses (atomic masses) to very large molecules (MDaltons) with detection limits down to the pico-, femto-, and attomole levels5. Furthermore, this analytical technique has become of great importance within the last decade or so due to advancements enabling even higher sensitivity and its ability to be combined with high-throughput automation for -"omics" studies with high applicability in drug discovery.
Sample Preparation
Samples for ESI-MS are typically purified, which is ideal for the instrument because mixtures of components with different physicochemical properties are not good analytes for the technique (e.g. glycans vs. peptides)1. Methods such as high-performance liquid chromatography, capillary electrophoresis, and liquid-solid column chromatography are commonly employed for the purification step, and subsequently injected into the ESI-MS1. Usually, the purification method is attached directly to the capillary needle1.

Electrospray Ionization (ESI)
A mechanical syringe pump injects the liquid sample (usually less than one mM in a polar volatile solvent) into the capillary needle, and thereby nebulizing it into a fine mist1. Typically an analyte will undergo three major processes after injection and transfers into the gas phase: it will produce charged droplets from the high-voltage cappillary tip, repeatedly evaporate solvent from the charged droplet followed by droplet disintegration into much smaller droplets, and lastly transfer of the ion into the gas-phase5. The capillary needle typically has an inner diameter of ~0.1mm and outer diameter of ~0.2mm, and a low flow rate around 1 to 20 μL/min1. A voltage is applied to the tip of the capillary of around 2-6 kV, where the surrounding source-sampling cone is located around 1-3 cm from the spray needle tip (see Figure \(\PageIndex{1}\))2.
The strong electric field causes the nebulized particles to carry a charge, thus, becoming electrospray droplets where a drying or sheath gas flows around the capillary improving nebulization1.
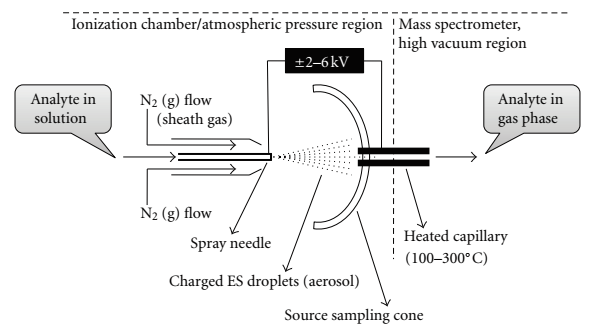
The electric field also directs the spray toward the mass spectrometer while droplets diminish in size (solvent evaporation)1. This process is described pictorally in Figure \(\PageIndex{3}\) below. Once the electrospray droplets pass through the heating capillary (Figure \(\PageIndex{2}\), labeled as desolvating capillary in Figure \(\PageIndex{1}\)), the ions completely desolvate1. The heating capillary is typically around 0.2mm inner diameter, 60mm in length, at a temperature controlled in a range from 100-300oC for desolvation and continual droplet shrinkage1. At this point two forces become dominant: surface tension in the droplets acting to retain the shape of the droplet, and Coulomb force of repulsion between like charges on the surface which act to break down the shape of the droplet2.
As the droplets travel through the heating capillary, they have a high enough electric field density that causes like charges to repel one another, increasing surface tension (first to second step in Figure \(\PageIndex{3}\))2. The droplets then reach the Rayleigh limit, which describes the limit of the number of charges that can be present on a charged droplet before fission occurs and is broken down (third step in Figure \(\PageIndex{3}\))1. It is at this point the surface tension can no longer sustain the Coulomb force of repulsion, and a “Coulomb explosion” or “Coulomb fission” occurs (fourth step in Figure \(\PageIndex{3}\))1. The parent droplets disintegrate into much smaller droplets of positive or negative charge, with a much higher mass-to-charge ratio1. These small droplets have high mass-to-charge ratios because smaller portions of parent charges are carried off and distributed in many offspring droplets compared to the mass carried off from parent droplets. An example time history is shown below of methanol droplets produced by electrospray in Figure \(\PageIndex{4}\).


The decomposition of a droplet from ESI occurs in manner similar to the inset of Figure \(\PageIndex{4}\), and is dictated by the Rayleigh equation:
\[q^2 = 8 \pi^2 \epsilon_o \gamma D^3 \label{1}\]
Where q is charge, epsilon 'naught' is the permissivity of the medium, gamma is the surface tension of the droplet, and D is the droplet diameter.
Mass Analyzers
From the ion beam, the mass analyzer takes different types of ions and separates them based on their mass-to-charge ratio. Afterwards, the ions are passed onto the detector. There are many types such as magnetic (B)/electric (E) sector mass analyzers, linear quadrupole ion trap (LIT), three-dimensional qudrupole ion trap (QIT), orbitrap (Mass Analyzer Orbitrap), time-of-flight mass analyzer (TOF, Mass Analyzer Time of Flight), and ion cyclotron resonance mass analyzer (ICR)1. They all take advantage of dynamic of static magnetic/electric fields based on Lorentz force law (Equation (1), a charge experiences electric and magnetic forces when traveling through magnetic/electric fields)3 and Newton's second law of motion (Equation (2), objects accelerate based on their mass and net forces acting on the object)4.
\[F = qE + qv x B \label{2}\]
\[F = m x a \label{3}\]
Where in Equation (2), F is the Lorentz force, q is the charge of the ion, E is the electric field, v is the velocity of the ion, and B is the magnetic field. In Equation (3), F is Force, m is mass, and a is acceleration.
Table 1 below briefly summarizes comparisons between different mass analyzers. The mass analyzer uses electrostatic lenses (see Figure \(\PageIndex{1}\)) to direct the beam into the analyzer, and is kept at a high vacuum (around 10-3 torr to 10-6 torr pressure) to prevent any undesired molecular interactions between the ions and the atmosphere1.
Table 1: Comparison of mass analyzers (de Hoffmann & Stroobant, 2007)
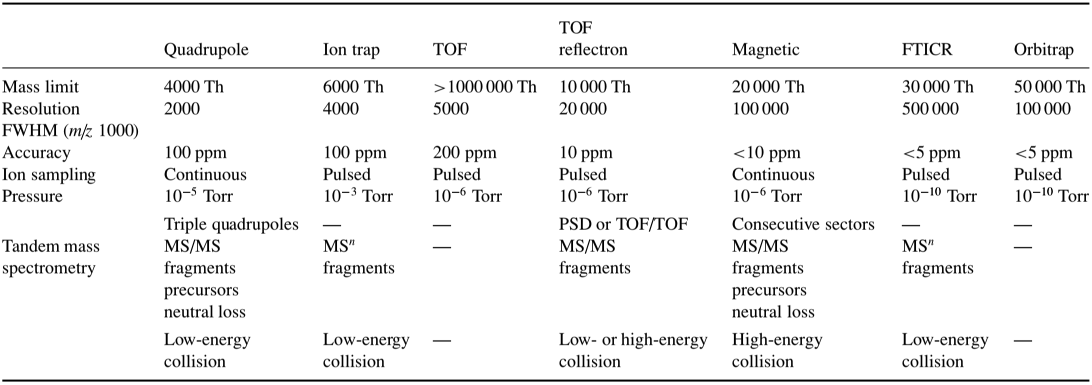
Five main characteristics for the measuring performance of a mass analyzer are the mass range limit, analysis speed, transmission, mass accuracy, and resolution5. According to de Hoffmann and Stroobant, mass range is the mass-to-charge (m/z) limit the mass analyzer can measure ions, expressed in units of Th (Thomson), or u (unified atomic mass unit) for ions with an elementary charge (z=1), where
Where m is the mass of the first peak, divided by the difference, ∆m, between the neighboring peaks2. The data is improved with more resolution (higher R)5.
Detectors
A common type of detector used in conjunction with a quadrupole mass analyzer for example, is an electron multiplier (EM) detector5. In this type of detector electrons are accelerated to a high velocity, enhancing detection efficiency5. To achieve this, an electrode called a conversion dynode is held at a high potential from + 3 kV to + 30 kV, opposite to the ions’ charges5. Once ions strike the conversion dynode, several secondary particles are emitted5. Secondary particles are typically negative and positive ions, electrons, and neutral particles5. For example, if positive ions strike the conversion dynode, negative ions and electrons are the secondary particles of interest, likewise, if negative ions strike the conversion dynode the secondary particles are positive ions5. The secondary particles are then amplified in a cascade effect to produce a current5.

Figure \(\PageIndex{8}\) shows a schematic for a discrete dynode electron multiplier detector5. The first dynode starts at a higher magnitude potential (but negative), causing the secondary particles to emit electrons5. The secondary particles and electrons accelerate to each subsequent dynode (due to the lower potential) until the electrons reach the output of the electron multiplier, which is held at ground potential5. A cascade of electrons are created at the end, and the current produced and amplified by conventional electronic amplification5.
Electrospray Ionization on Membrane Proteins
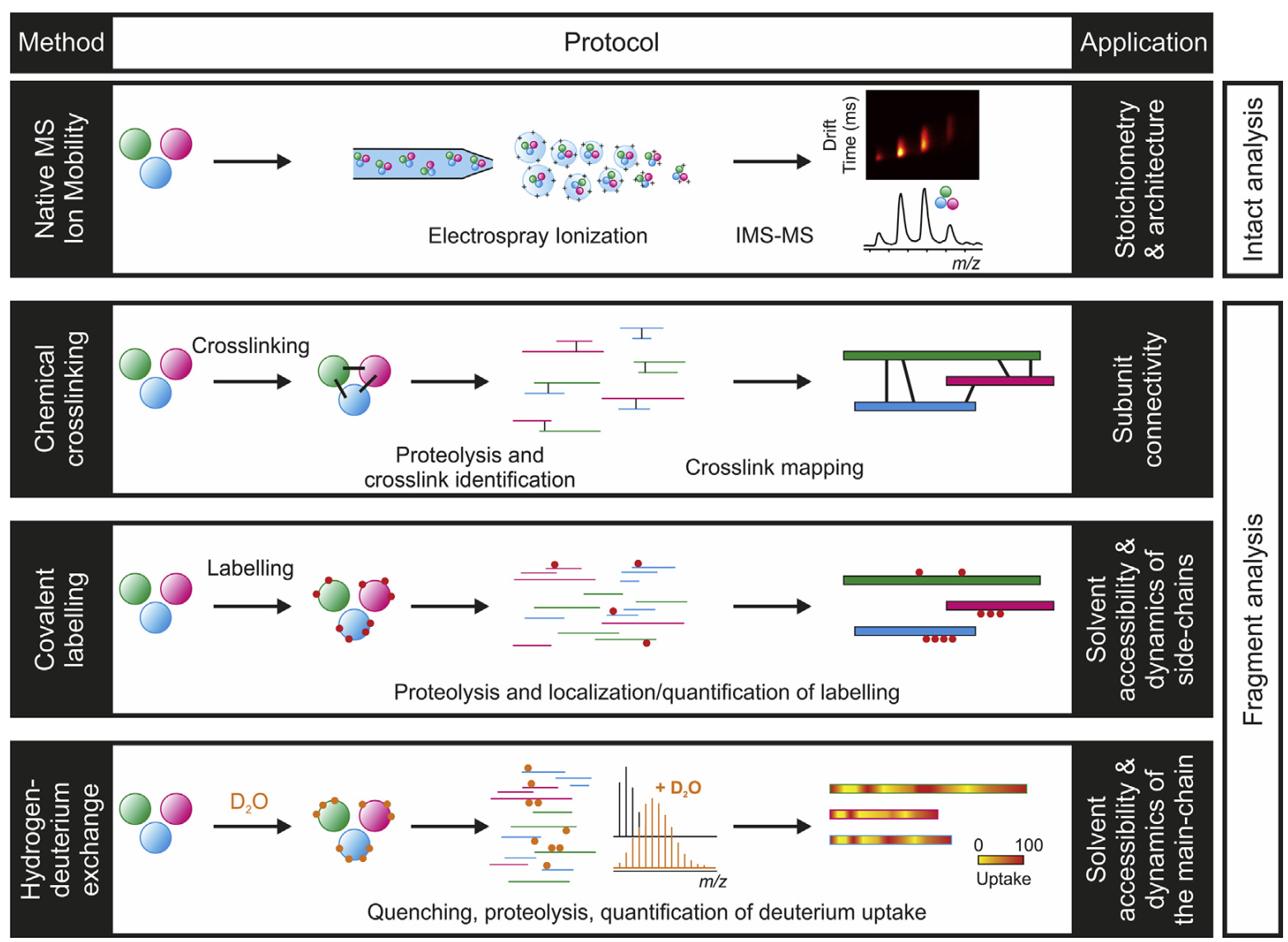
Membrane proteins are of particular interest because of their importance in cell signaling, transport, adhesion6, and intercellular interactions. Some advantages of mass spectrometry methods in studying membrane proteins are that freezing or crystallization (as in X-ray crystallography) are not required, and that it is possible to study these proteins in their native (unfolded) state6. Utilization of electrospray ionization (ESI) mass spectrometry (MS) on membrane proteins typically falls under two categories: native MS and labeling MS6. Native MS involves maintaining non-covalent interactions, which preserves tertiary and quaternary structures, and is carried out in vacuo6. Labeling MS methods involve chemical crosslinking, hydrogen-deuterium exchange, and hydroxyl radical footprinting (HRFP) to name a few6. For each method, proteins are labeled in solution (peptides reacted with chemical labels), undergo proteolysis, and are subsequently measured/quantified via MS method6 (see Figure \(\PageIndex{9}\) below).
Considerations for ESI on Membrane Proteins
Careful consideration in optimizing the parameters are absolutely necessary when analyzing biological materials in mass spectrometric methods. Two examples of these parameters are the collision voltage and selection of detergent6. The collision voltage is that which is applied to molecular ions, accelerating them into the collision cell with an inert gas5. Optimization of collision voltage involves selecting a voltage that enables fragment ions to be observed, but also well resolved. This voltage goes hand-in-hand with careful consideration of the buffer/detergent. Ideally, the buffer/detergent needs to be able to efficiently solubilize the protein, and also be easily removed to allow the protein to be properly desolvated (see Figures 3 and 4)6. Detergents are used for membrane proteins because of their amphiphilic nature, similar to the membrane proteins themselves6. Where these two parameters come together are when the membrane protein-detergent complex transfers into the gas phase: the collision voltage must be high enough to desolvate the membrane protein from the detergent, and the detergent must not strongly solvate the membrane protein6. Strong solvating detergents require higher energies which risk destabilizing the protein prior to detection in the mass analyzer.
If the membrane protein is not liberated from the detergent, perhaps due to low collision voltage, the membrane proteins' signals maybe be suppressed by noise from the remaining detergent (see Figure \(\PageIndex{1}\)0b and 10f). Figure \(\PageIndex{1}\)0 below also demonstrates the concepts of selecting proper collision voltage combined with an appropriate detergent.

Summary
- Electrospray (ESI) is a soft-ionization technique that has gained popularity in biological applications as it is capable of maintaining non-covalent interactions of proteins.
- Use of appropriate buffers/detergents/optimized instrument conditions renders ESI-mass spectrometry (MS) to be a powerful and sensitive tool to elucidate membrane protein structures.
- ESI can be coupled with a variety of mass analyzers (see Table 1), providing users of mass spectrometry flexibility in analysis.
- ESI can also be coupled downstream from a variety of chromatographic techniques such as HPLC to enhance mass spectrometry-based studies on complex molecular structures.
References
- Banerjee, S., & Mazumdar, S. (2012). Electrospray Ionization Mass Spectrometry: A Technique to Access the Information beyond the Molecular Weight of the Analyte. International Journal of Analytical Chemistry.
- Murphy, J. (2016, October 8). Electrospray Ionization Mass Spectrometery. Retrieved from Chemistry LibreTexts(TM): https://chem.libretexts.org/Core/Ana...s_Spectrometry
- Bird, R. B., et al. (2001). Transport Phenomena, Wiley.
- Young, H. D., Freedman, R. A., & Sears, F. W. (2004). Sears and Zemansky's university physics (11th ed.). San Francisco, Calif.: Pearson/Addison Wesley.
- de Hoffmann, E., & Stroobant, V. (2007). Mass Spectrometry Principles and Applications. West Sussex, England: John Wiley & Sons, Ltd.
- A.N. Calabrese, S.E. Radford, Methods (2018). https://doi.org/10.1016/j.ymeth.2018.02.020
- Dempster, A. J. (1921). "Positive Ray Analysis of Lithium and Magnesium." Physical Review 18(6): 415-422.
- McFarland, S. (Ed.). (2008, April 19). File:Fission.jpg. Retrieved June 13, 2018, from http://www.appropedia.org/File:Fission.jpg
- Bird, R. B., et al. (2001). Transport Phenomena, Wiley.
- (2003). University Physics With Modern Physics,11/e, Pearson Education.
Contributors and Attributions
- Christopher Ranque

