S24. Big Bang Nucleosynthesis: Predictions

Last updated
Save as PDF

Page ID: 32749

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Exercise 24.1.1

Answer

From \(n + \nu_e \longleftrightarrow p + e^{-}\) being fast we can conclude that

\[\ \mu _n + \mu _{\nu_e } = \mu_p +\mu_{e^{-}}.\]

Due to the arguments given above that \(\mu _{\nu_e } = 0\) and \(\mu_{e^{-}}=0\) we can thus conclude that \(\mu_n = \mu_p\).

Exercise 24.2.1

Answer

In the non-relativistic and dilute (\(f <<1\) for most particles) limits we can neglect the \(\pm 1\) factor in the denominator of \(f\) so we get the same result for both bosons and fermions:

\[\begin{equation}
n = g\left(\frac{mc^2 k_BT}{2\pi \hbar^2 c^2}\right)^{3/2} \exp\left[-(mc^2-\mu)/(k_BT)\right] \\
\end{equation}\]

Both protons and neutrons have the same g and because of the proton-neutron inter-converting reactions are fast (and other assumptions given) our rule for fast reactions leads to neutrons and protons having the same chemical potential, \(\mu\). They are also in kinetic equilibrium with each other so have the same \(T\). Taking the above equation for protons, with \(m= m_p\) and the above equation for neutrons, with \(m=m_n\) and using them to calculate \(n_n/n_p\) one gets Eq. 24.7.

Exercise 24.3.1

Answer

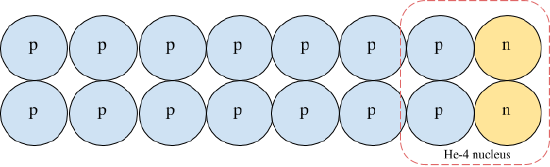
The fraction of baryonic mass in Helium is 4/16 = 0.25.

Exercise 24.4.1

Answer: I don't have the sketch here, but neutron-proton freezeout happens at a temperature such that \(k_BT = 0.8\) MeV and the deuterium bottleneck ends at about \(k_B T = 0.06\) MeV. The neutron to proton ratio changes from 1/5 to 1/7 between these two times. The ratio decreases due to neutron decay.

Exercise 24.5.1

Answer: If G were larger then the expansion rate would be faster (via the Friedmann equation). Because of this, neutron-proton freeze-out would happen at a higher temperature, which means the ration of neutrons to protons would be higher. It would also take less time to cool down to \(k_B T = 0.06\) MeV (because of the more rapid expansion) which would reduce the amount of neutron decay that occurs. Both of these effects would increase neutron abundance at the end of the deuterium bottleneck so Helium production would increase; i.e., \(Y\) would be larger.