2: Curvature
- Page ID
- 5103
We introduce the notion of "curvature'' in an attempt to loosen up your understanding of the nature of space, to have you better prepared to think about the expansion of space.
About 2300 years ago Euclid laid down the foundations of geometry with 23 definitions and five postulates. This was all done in an attempt to capture what were obvious fundamental properties of space, so that they could be used as starting points to prove other things about space -- such as that the sum of the angles of a triangle is 180 degrees, and that the ratio of a circle's circumference to diameter is the same for all circles. The first four postulates could be put rather succinctly. The fifth one though is a bit unwieldy. In translation from the original Greek, taken from Wikipedia, we have [in two-dimensional geometry]:
If a line segment intersects two straight lines forming two interior angles on the same side that sum to less than two right angles, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles.
There were many attempts to prove this fifth postulate, also known as the "parallel postulate" from the other four. Eventually it was realized that it can't be done.
We have also come to experimentally determine that space is different from what one gets with all five of Euclid's axioms together. Our theoretical understanding of the nature of space (consistent with all measurements) allows for the possibility that two lines as described in the fifth postulate might never meet, on either side of the line they both intersect. Throwing out this fifth postulate leads to the possibility that the angles of a triangle sum up to something different from 180 degrees, and that the ratio of circumference to diameter of a circle can vary depending on location of the circle center and the size of the circle.
The ratio of circumference to diameter that is different from \(\pi\) is a signature of a property called "curvature." Euclidean geometry is a geometry with zero curvature. In this section we will study both two and three-dimensional curved (and therefore "non-Euclidean") spaces. One way we will gain some intuition about these spaces is by embedding them in a Euclidean space of one extra dimension. We will emphasize here that there need not be any physical reality to the extra-dimensional space. We can describe curved spaces mathematically without any reference to extra dimensions. Space can "curve" without having to "curve into" any external space. Coming to terms with this idea will, perhaps, make you more comfortable with the idea that space can expand without expanding into anything else.
Let's get started.
We can label space with coordinates, for example, we could label every point in a 2-dimensional space with an \(x\) value and a \(y\) value. These coordinates are just labels, with no physical meaning, until we also say something about the distance between infinitesimally separated pairs of points. For example, in a two-dimensional Euclidean space with which you are familiar, the square of the distance between \(x,y\) and \(x+dx,y+dy\) is given by:
\[d\ell^2 = dx^2 + dy^2 \label{eqn:EuclidCartesian} \]
The physical interpretation of \(d\ell^2\) is as follows:
The length of a ruler with an end on each of the two points is \(\sqrt{d\ell^2}\).
Expressions for the distance are not always as simple as the one above. Even for the same physical space, with different coordinate schemes the equation for \(d\ell^2\) will look different. For example, we could choose polar coordinates instead of Cartesian ones and then distances would be given by:
\[d\ell^2 = dr^2 + r^2 d\phi^2 \label{eqn:EuclidPolar} \]
This is the same space, just described with different coordinates.
Note that one can find the distance along any path through the space by calculating \(\int d\ell\) along the path.
The space we are describing in this chapter so far (and its higher- and lower-dimensional versions) we call "Euclidean" because these spaces are consistent with geometry as described by Euclid. It turns out though that space is not Euclidean (although a Euclidean description is often a very good approximation). This is a bit startling. If you are not startled by it, you don't understand it yet. But don't worry; you will. And hopefully your mind will be blown.
From Einstein we learned that space can be quite different from Euclidean. To begin to free your mind from its Euclidean constraints, let's consider a non-Euclidean space that we label with \(r\) and \(\phi\) using the same construction as we outlined in the previous chapter. The construction is exactly the same, but the strange nature of the space is revealed by this different rule for the distance, \(d\ell\), between \(r,\phi\) and \(r+dr,\phi+d\phi\):
\[d\ell^2 = \frac{dr^2}{1-kr^2} + r^2 d\phi^2 \label{eqn:two-sphere} \]
At the moment, the introduction of the \(1-kr^2\) factor should just look arbitrary. We will eventually derive this distance rule from an assumptions of homogeneity and isotropy of the space. For now, let's explore its geometrical implications.
For the three following boxes (four exercises) assume the space is one governed by the distance rule of Eq. \ref{eqn:two-sphere}.
Box \(\PageIndex{1}\)
Exercise 2.1.1: How long would a path be that stretches from \(r=0\) to \(r=r_1\) at constant \(\phi\)? Call the length \(\ell\) and express it as an integral that depends on \(r_1\) and \(k\). Assume that \(r_1\) is much less than \(\sqrt{1/k}\). Make a Taylor expansion that approximates the integrand so that it contains the first order corrections due to \(k \ne 0\). After this approximation, do the integral. [Hint: many students in my experience have trouble with this Taylor expansion, hence this hint. Use this first order Taylor expansion result: \( (1+ \epsilon)^n = 1+n\epsilon\) where \(\epsilon \) is some small number and apply it to the term \(\sqrt{1/(1-kr^2)}\).]
Box \(\PageIndex{2}\)
Exercise 2.2.1: Consider the set of points all at \(r= r_1\) with all values of \(\phi\). Is this a circle? What is the circumference of this object as a function of its radius, \(\ell\)? Recall that because of how the coordinate system was constructed, you can assume that \(r,\phi\) and \(r,\phi+2\pi\) are the same point. First find the circumference as a function of \(r_1\) and then use your result from the previous problem to express it as a function of \(k\) and \(\ell\). [Don't get too hung up on solving for \(\ell\) as a function of \(r_1\). If you take advantage of some additional appropriate approximations the algebra is not too bad, but don't spend too much time trying to figure it out.]
Exercise 2.2.2: Discuss the result from Exercises 2.1.1 and 2.2.1 and what it means qualitatively for the circumference-radius relationship for circles in spaces with \(k < 0\), \(k > 0\) and \(k=0\). [Note that you can do this even if you did not manage to get \(\ell\) as a function of \(r\) in the above exercise.]
Box \(\PageIndex{3}\)
Exercise 2.3.1: If you were a two-dimensional creature, and could travel around this space with a measuring tape, describe in a few sentences at least one way for measuring the value of \(k\).
Embedding
Sometimes it is possible to visualize a non-Euclidean space, such as the one with invariant distance rule given by Equation \ref{eqn:two-sphere}, by embedding it in a higher-dimensional Euclidean space. Such an embedding, into a space with one extra dimension, is shown in the figure for \(k>0\). When using such an embedding diagram it is important to keep in mind that there are extra dimensions in the diagram whose sole purpose is visualization -- they have no physical significance. In the figure here, the space we are describing is the two-dimensional sphere; the radial dimension is fictional, included here only for purposes of visualization.
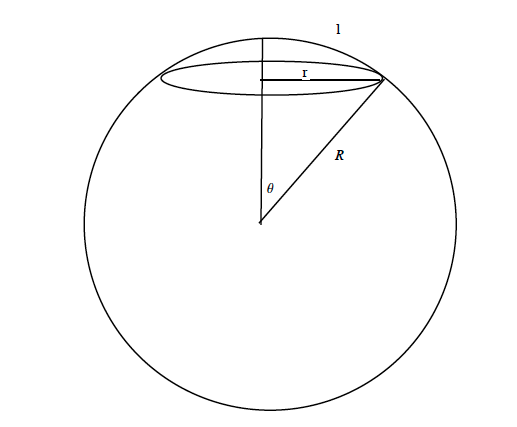
Note that every point on the sphere can be labeled by the latitude-like coordinate \(\theta\) and the longitudinal coordinate (not shown) \(\phi\). Also, at every point one can convert \(\theta\) and \(\phi\) to \(r\) and \(\phi\). In a homework problem you will derive Equation \ref{eqn:two-sphere} starting from the assumption that the three-dimensional space used for the embedding is Euclidean.
Box \(\PageIndex{4}\)
Exercise 2.4.1: Observe the circle at constant coordinate value \(r\) in the embedding diagram. The distance (traveled on a path restricted to the 2-dimensional space of the sphere), from the origin (top of the sphere) to any part of the circle, in the 2-dimensional space of the sphere, is \(\ell\). Is the circumference of the circle greater than, equal to, or less than \(2\pi \ell\)? Compare to the relevant result in the boxes above.
Not all spaces can be embedded by placing them in just one extra dimension. For example, the \(k<0\) space requires two extra dimensions for embedding. Part of the \(k < 0\) space is sometimes shown embedded in just one extra spatial dimension, with the two-dimensional surface having a shape similar to a saddle. One can start to see the problem here because if the diagram were extended, the saddle would curve into itself. Such self intersection can only be avoided by introduction of yet another fictional extra dimension.
Three-dimensional Homogeneous and Isotropic Spaces
Let us now take things up one dimension into 3-D.
Previously we asserted that one could label a 3-dimensional Euclidean space with coordinates \(r\), \(\theta\), and \(\phi\) such that points separated by \(dr\), \(d\theta\), and \(d\phi\) would be separated by a distance (as one would measure with a ruler) with square given by
\[ d\ell^2 = dr^2 + r^2\left(d\theta^2 + \sin^2\theta d\phi^2\right) \]
A space that can be labeled in this way is homogeneous (invariant under translations) and isotropic (invariant under rotations). The easiest way to see this is to remember that there's a coordinate transformation to Cartesian coordinates for which
\[d\ell^2 = dx^2 + dy^2 + dz^2\]
Now the homogeneity is more evident, since transforming \(x\) to \(x' = x + L\) would clearly leave the distance rule unchanged. We've also already seen that rotations leave the distance rule unchanged. So, the space is homogeneous and isotropic. If we choose to label it with spherical coordinates about a particular origin, our labeling obscures the homogeneity and isotropy, but the space itself is still homogeneous and isotropic.
It turns out that whether one can label space in this way or not is a matter to be settled by experiment. It's not necessarily true. Even if we restrict ourselves to completely homogeneous and isotropic geometries, we can mathematically describe spaces that cannot be labeled in this way.
What is generally true is that all three-dimensional homogeneous and isotropic spaces can be labeled with coordinates \(r\), \(\theta\), and \(\phi\) such that
\[d\ell^2 = \dfrac{dr^2}{1-kr^2} + r^2\left(d\theta^2 + \sin^2\theta d\phi^2\right)\]
for \(k\) a constant that can be positive, negative or zero. Euclidean space is a special case with \(k=0\).
BOX \(\PageIndex{5}\)
Exercise 2.5.1: You know that in a Euclidean space the relationship between radius and area of a sphere is \(A = 4\pi r^2\) with \(r \) specifying the radius. Note that the angular ( \(d\phi\) and \( d\theta\) ) parts of the invariant distance equation are unchanged by having \(k \ne 0\). Therefore we still have \(A = 4\pi r^2\) even if \(k \ne 0\). I also claim that the relationship between sphere area and radius does depend on \(k\). How can these statements both be true?
We can construct the homogeneous and isotropic three-dimensional space and derive its invariant distance rule, at least for the case of \(k>0\), by embedding it in a 4-dimensional Euclidean space. In a 4-dimensional Euclidean space we can have a coordinate system consisting of three dimensions \( x, y, z\), that are all orthogonal to each other, and a fourth we will call \( w \) that is orthogonal to each of the \(x, y,\) and \( z\) directions. Impossible as this is to visualize, we can describe it mathematically. The distance between \(w,x,y,z\) and \(w+dw,x+dx,y+dy,z+dz\) is given by
\[d\ell^2 = dw^2+dx^2+dy^2+dz^2.\]
In this 4-dimensional space, we construct a three-dimensional subspace that is the set of points all the same distance, \(R\), from a common center. Let's center it on the origin so our subspace satisfies this constraint:
\[w^2 + x^2 + y^2 + z^2 = R^2.\]
This subspace is homogeneous (all points are the same) and isotropic (all directions are the same). You can see that this is true by imagining it's two-dimensional analog, a sphere, which is the set of all points satisfying \(x^2+y^2+z^2 = R^2\).
It will be helpful at this point to swap out the Cartesian \(x,y,z\) for the spherical coordinate system \(r,\theta,\phi\) so we have
\[d\ell^2 = dw^2 + dr^2 + r^2(d\theta^2 + \sin^2\theta d\phi^2)\]
and our constraint equation can be written as
\[w^2 + r^2= R^2. \]
From this new version of the constraint equation, we can see that if \(r\) changes by some amount then we will necessarily have to have a change in \(w\) in order to continue to satisfy the constraint. The exact relationship between differential changes you can easily work out to be \(2wdw+2rdr = 0\) (because changing \(r\) by \(dr\) ends up changing \(r^2\) by \(2rdr\) and likewise for \(w\) and \(dw\) and since \(R\) is fixed \(dR^2 = 0\)). Using this relationship to eliminate \(dw^2\) from our invariant distance expression, and using the constraint equation to eliminate \(w^2\) in favor of \(r^2\) and \(R^2\) we get
\[d\ell^2 = \frac{dr^2}{1-r^2/R^2} + r^2(d\theta^2 + \sin^2\theta d\phi^2).\]
We see that our subspace has an invariant distance expression of the form we were intending to derive, and it is exactly the one introduced above if we make the identification \(R^2 = 1/k\).
Summary
Let us now summarize the key points in our study of spatial geometry. First, the most general, high-level points:
- We can label the continuum of points in a space with coordinates.
- These coordinates have no physical meaning on their own.
- Physical meaning comes from the combination of the coordinates and a rule for converting infinitesimal coordinate differences into an infinitesimal distance.
Now let's summarize at a greater level of detail:
- We studied two-dimensional and three-dimensional homogeneous and isotropic spaces. Homogeneity means the spaces are the same everywhere; e.g., no matter where one is in the space, one would find the same relationship between circumference and radius of circles. Isotropic means that there are no special directions in the space.
- We labeled such spaces with polar (for 2D) and spherical (for 3D) coordinates. We used an explicit construction for the 2D case. We defined the radial coordinate as a ``circumferential coordinate'' that gives a circumference for a circle as equal to \(2\pi r\) by definition. We defined the angular coordinate \(\phi\), in the 2D case, so that the distance from \(r, \phi\) to \(r, \phi + d\phi\) is equal to \(r d\phi\). Since the circumference is \(2\pi r\) this means \(r, \phi\) and \(r, \phi + 2\pi\) are the same point.
- We first asserted that a 2D homogeneous and isotropic space with coordinates constructed as above has the following distance rule: \(d\ell^2 = dr^2/(1-kr^2) + r^2 d\phi^2\), where \(k\) is some constant with units of inverse area. We also asserted that in the 3D case the distance rule in spherical coordinates (with an analogous construction procedure that we did not explicitly describe) is \(d\ell^2 = dr^2/(1-kr^2) + r^2 (d\theta^2 + \sin^2{\theta} d\phi^2)\).
- Partly to demonstrate that these are indeed homogeneous and isotropic spaces, we then demonstrated how such a space could be constructed, for the case of \(k > 0\), by embedding it in a Euclidean space with one additional dimension. We were able to visualize such an embedding for the 2D case. Although we could not visualize the embedding in the 3D case, we at least mathematically treated its embedding in a 4D Euclidean space to derive the distance rule.
We also introduced techniques for doing geometrical calculations. We introduced paths through a space described by use of an independent parameter; e.g., \(x(\lambda) = \lambda, y(\lambda) = \lambda\) with \(\lambda\) ranging from 0 to 1. If these are Cartesian coordinates in a 2-dimensional Euclidean space then this describes a straight line from \((0,0)\) to \((1,1)\). We calculated distances along such parameterized paths by calculating \(\int ds = \int d\lambda (ds/d\lambda)\) from one endpoint of the path to another. Continuing with our example, that's length = \(\int_0^1 d\lambda \sqrt{ (dx/d\lambda)^2 + (dy/d\lambda)^2} = \int_0^1 d\lambda \sqrt{1 + 1} = \sqrt{2}\). We also reminded you of a result from the calculus of variations, that you have seen in your study of classical mechanics, and applied it to such length integrals, in order to derive the differential equations obeyed by extreme paths, which are usually (but not always) the shortest paths.
We used these calculational techniques to calculate circumferences and radiuses of circles in the 2D case. With our exploration, in this way, of homogeneous and isotropic spaces, our fervent desire is that your mind is now freed somewhat from its Euclidean intuitions about the nature of space. If you can imagine that the area interior to a circle can be larger than \(\pi r^2\), where \(r \equiv C/(2\pi)\) and \(C\) is the circumference, or the volume interior to a sphere can be larger than \(4/3 \pi r^3\) where \(r^2 = A/(4\pi)\) and \(A\) is the surface area, then you are now better prepared to contemplate the expansion of space.
The expansion of space happens over time. In the next two chapters we thus turn our attention to the geometry of spacetime. We'll find in Chapter 4 that spatial distances are no longer invariant under changes of coordinate systems; you may have been exposed to this before via the phenomenon of Lorentz contraction. We'll therefore be forced to alter how we relate coordinate differences between infinitesimally separated pairs of points to things we can actually measure. In particular, for this purpose, we will introduce the ``invariant distance'' that presumably you have studied in special relativity.
HOMEWORK Problems
For the homework problems we will be considering a two-dimensional space labeled with coordinates \(r\) and \(\phi\) with invariant distance given by
\[\begin{equation*}
\begin{aligned}
d\ell^2 = \frac{dr^2}{1-kr^2} + r^2 d\phi^2
\end{aligned}
\end{equation*}\]
In the following, assume \( k > 0 \) unless otherwise specified.
Problem \(\PageIndex{1}\)
How long is the path that runs from \(r=0\) to \(r=r_1\) at constant \(\phi\)? Call the length \(\ell\) and express it as a function of \(r_1\) and \(k\). Assume that \(r_1 < \sqrt{1/k}\). Unlike in the exercises, do not use a Taylor series approximation to \(1/(1-kr^2)\).
Problem \(\PageIndex{2}\)
Consider the set of points all at \(r= r_1\) with all values of \( \phi\). This set is a circle since it is the set of all points located a particular distance away from another point ( \(r=0\) ). What is the circumference of the circle? First find the circumference as a function of \(r_1\) and then use your result from the previous problem to express it as a function of \(k\) and \(\ell\).
Problem \(\PageIndex{3}\)
If you were a two-dimensional creature, and could travel around this space with measuring tape, describe in a few sentences at least
one way for measuring the value of \(k\).
Problem \(\PageIndex{4}\)
Consider the embedding diagram in the chapter. Keep in mind that the 3-dimensional space, in which the 2-dimensional sphere is embedded, is Euclidean. Use what you know about Euclidean geometry to show that the square of the length of the path between \(r,\phi\) and \(r+dr, \phi+d\phi\), constrained to lie in the sphere, is indeed given by \( \frac{dr^2}{1-kr^2} + r^2 d\phi^2 \) for the appropriate choice of \(k\) as a function of the radius of the sphere \(R\). Also specify that function.
Don't let this calculation lead you astray conceptually. Although it's perfectly fine, and a useful tool for visualization, to consider a two-dimensional space embedded in a three-dimensional Euclidean space, one can have curved two-dimensional spaces without there needing to be a third dimension. We see this mathematically in this chapter as we can do things like calculate observables (lengths) without any reference to an additional (third) dimension.
Problem \(\PageIndex{5}\)
Fun with the Schwarzschild solution. The space outside of a central spherically symmetric mass distribution can be labeled with coordinates \(r,\theta,\phi\) such that
\[\begin{equation*}
\begin{aligned}
d\ell^2 = (1-r_s/r)^{-1} dr^2 + r^2\left(d\theta^2 + \sin^2\theta d\phi^2\right)
\end{aligned}
\end{equation*}\]
where \(r_s = 2GM/c^2\) is the "Schwarzschild radius" and \(M\) is the total mass of the mass distribution. The azimuthal angle \( \phi \) runs from 0 to \( 2\pi\). For the Earth, \(r_s \) is about 9 mm.
Consider two concentric circles in the same plane with centers at the center of the mass distribution ( \(r=0\) ). If the spatial geometry were Euclidean, the differences in their circumferences would be \(\Delta C = 2\pi \Delta \ell\) where \(\Delta \ell\) is the radial distance between the two circles. But the presence of the mass means the spatial geometry is not Euclidean, and instead given by the Schwarzschild solution. If the two circles are at coordinate values \(r_1\) and \(r_2\), show that, for \(r_s\) much smaller than \(r_1\) or \(r_2\) one instead gets \(\Delta C = 2\pi \Delta \ell\ - \pi r_s \ln(r_2/r_1) \). Hints: 1) Choose the circles so that it's just \(\phi\) that's changing, with \( \theta \) fixed to \( \pi/2 \) and 2) Taylor expand to first order so \(\sqrt{(1-r_s/r)^{-1}}\) = \(1+\frac{1}{2}\frac{r_s}{r}\).
Note that if we take \(r_2\) to be 42,000 km (about the distance to geostationary orbit from the center of the Earth) and \(r_1\) to be 6,000 km (the distance from center of Earth to the surface), the correction to the difference in the circumferences is \( \pi r_s \ln(r_2/r_1) \)= 11 cm. A very small correction! The spatial geometry around Earth is very close to Euclidean.


