1.2: Electric Field
- Page ID
- 17297
Coulomb Field
While one can describe the details of forces between charges mathematically, it still is very unsatisfying – how do the charges affect each other from a distance? This question troubled physicists for a long time, and the “solution” (really it is just a model that works) is quite ingenious. It goes like this:
The source of the electric (or for that matter, gravitational) force doesn’t know anything about the existence of another charge “out there.” All it knows is its own charge. The source then sends out a “signal” that radiates away from it radially, and this signal carries with it the information of how much charge the source has and how far the signal travels – the signal gets weaker as it gets farther from the source, because it spreads out on the surface of an ever-growing sphere. Now if another charge happens to be in the space near where this source is, it “receives” the signal, and it takes from it the information about the amount of charge of the source, as well as the signal strength itself (which includes the inverse-square-law separation information), and the direction from which the signal is coming. The affected charge puts all this information together with its own charge to determine the electric force it feels.
This “signal” is constantly emitted, so it is always everywhere in the space around the source charge, and it is called the electric field of that source charge. Since the signal carries information about both a magnitude (source charge and distance) and a direction (coming from the source charge's position), it essentially associates a vector with every point in space. Defining (as usual) the origin to be at the position of the source charge, the electric field vector at a specific point (defined by the position vector \(\overrightarrow r = r\;\widehat r\)) due to the source charge is:
\[\overrightarrow E = \dfrac{k\;q_{source}}{r^2}\;\widehat r \]
To visualize what the complete field looks like, imagine all of space filled with vectors. For a positive point charge, the vectors all point directly away from it, and the magnitudes of the vectors drop-off in length as they get farther from the source:
Figure 1.1.2 – Electric Field of a Point Charge
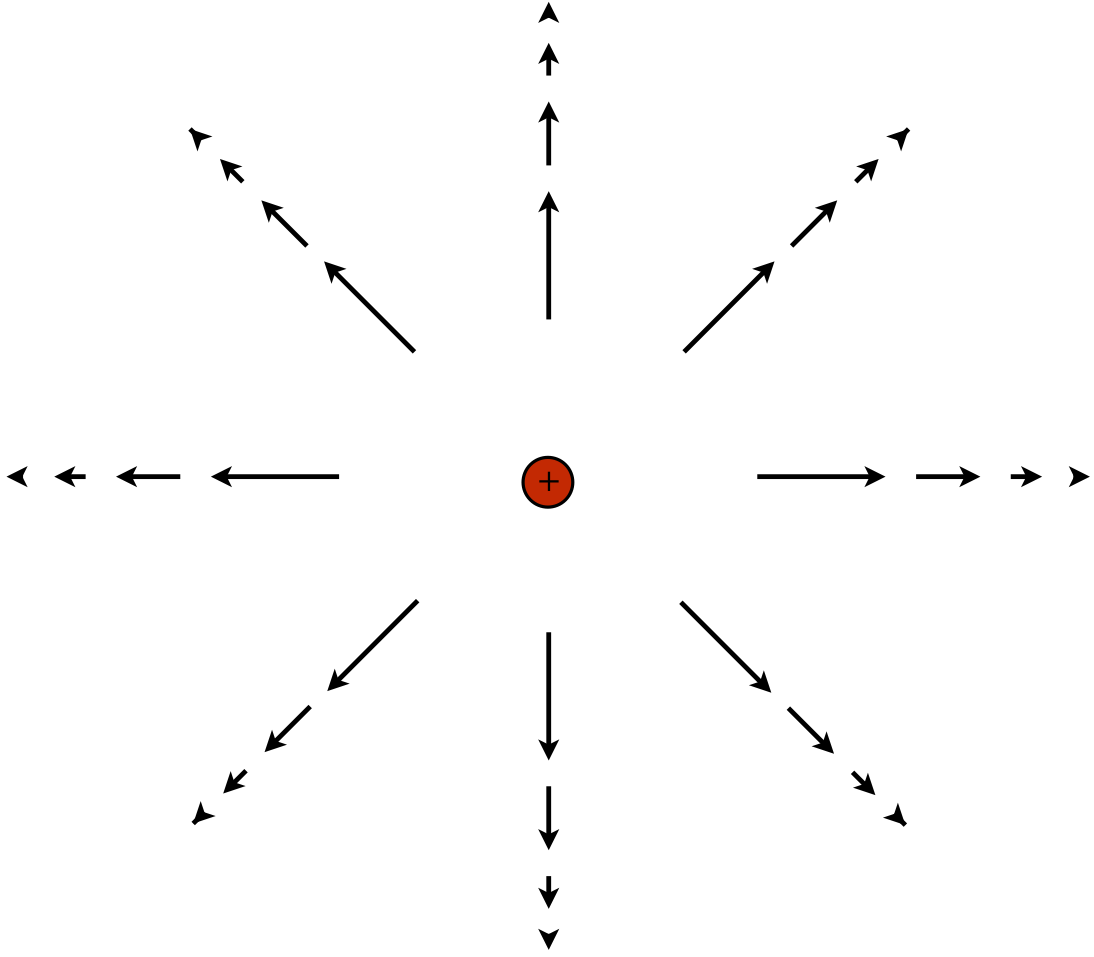
Comparing our Coulomb field equation with Equation 1.1.3, we see that indeed all of information needed to compute the electric force, except for the amount of charge that is affected, is contained within the electric field vector. So if we know the electric field vectors everywhere in space (or, more succinctly, we "know the electric field"), then we can compute the force on a point charge placed at any position, simply by multiplying the affected charge by the electric field vector:
Alert
It is a common mistake to think that the electric field vector points in the direction of the force acting on a charge, but the affected charge can be either positive or negative. If it is a positive charge, then the direction of the force on it will be the same as the direction of the field, but if the affected charge is negative, then the force and field will point in opposite directions.
Field Superposition
While the field model may be only slightly more satisfying than the direct action model from a philosophical standpoint, it actually has some very pragmatic uses. The foremost of these is that it allows us to talk about forces on a particle without having to actually worry about the specifics of all the other particles affecting it. Once we determine the electric field due to one or a collection of charges, we can forget about those charges and just work with the field. Wait… “collection of charges?” How do we determine the electric field of a collection of charges? It turns out that we can superpose field vectors to get a single, aggregate field vector. That is, we don’t have to worry about how a charge is affected by the electric fields of a whole lot of other charges – we can instead aggregate the electric fields of all those charges, and call it the electric field in that space, and use it alone to determine the force on the charge in question. To compute the electric field contributions of several charges at a single point in space, we naturally have to add them like vectors.
While it is often useful to picture electric fields as collections of lots of little vectors of varying length and direction filling all of space, there is also another descriptive way to think about electric fields. This is called electric field lines of force, or simply, electric field lines. What this picture does is to merge the field vectors together, so that lines are created that point the direction of the field everywhere in space. So for example, consider two point charges with equal magnitudes and opposite signs in the same region of space (such a configuration is called a dipole, while a single point charge is called a monopole):
Figure 1.2.2 – Dipole Field Lines
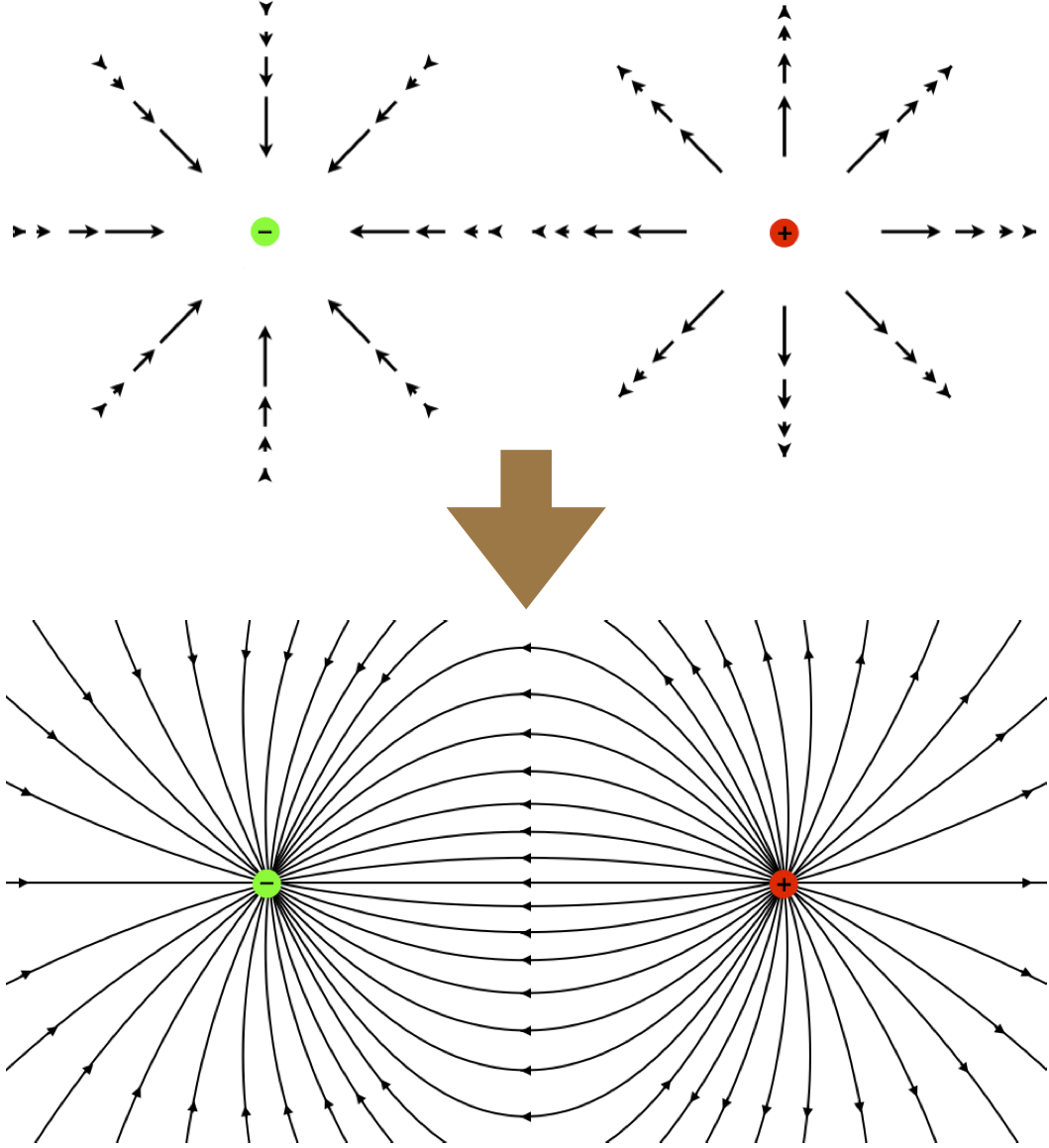
The field line description clearly displays the direction of the electric field vectors everywhere in space (tangent to the lines drawn, in the direction of the arrows). One might suppose that it is nonetheless inferior to the many-little-arrows picture, in that it doesn't display the strength of the field everywhere, but this is not correct. We know that the electric field get stronger as they get closer to the point charges, and there is a property of electric field lines that represents this – the density of field lines. The closer together the lines are, the stronger the field.
Consider the electric field lines for the dipole shown above along the horizontal axis joining the two charges. To the right of the positive charge, we notice that adjacent field lines are diverging from each other faster than if the positive charge was by itself (when they would emanate directly radially outward). With the density of the field lines indicating field strength, this means that the field is getting weaker in that direction faster than if the positive charge was the only source of the field. We already know how fast the field weakens with distance for a monopole (given in Equation 1.2.1), and in Section 1.4 we will approximate (for large values of \(r\) compared to the dipole charge separation) the faster rate at which this dipole field weakens with distance.


