1.3: Computing Electric Fields for Known Charge Distributions
- Page ID
- 17298
Continuous Charge Distributions
Charges occur in nature in discrete microscopic pieces. We can imagine a long line of charges, and the field that the superposition of fields of all these charges would create. If the charges are small enough and close enough together, the line of charge would look continuous. There are many examples of continuous collections of charge besides a linear string. For example, the string of charges doesn’t need to be in a straight line. Also, it doesn’t need to be distributed on a line at all, but can instead be spread across a surface or inside of a volume. These lines, surfaces, and volumes can take on an infinite number of shapes, although mathematically we can only really solve for the electric fields of the simpler, more symmetric ones, like straight lines, circles, planes, cylinders, and spheres.
The one aspect to solving such problems common to all of them is that in every case, we cease talking about individual charges and instead work with charge density. We discussed the idea of density in detail in both Physics 9A (e.g. mass density is used in calculating center of mass and rotational inertia) and Physics 9B (e.g. mass density of a medium affects the speed of a wave through it, and the density of a fluid plays a role in buoyancy). Here we are measuring charge-per-unit-whatever (the “whatever” being determined by the dimension into which the charge is distributed).
Figure 1.3.1 – Linear, Surface, and Volume Densities
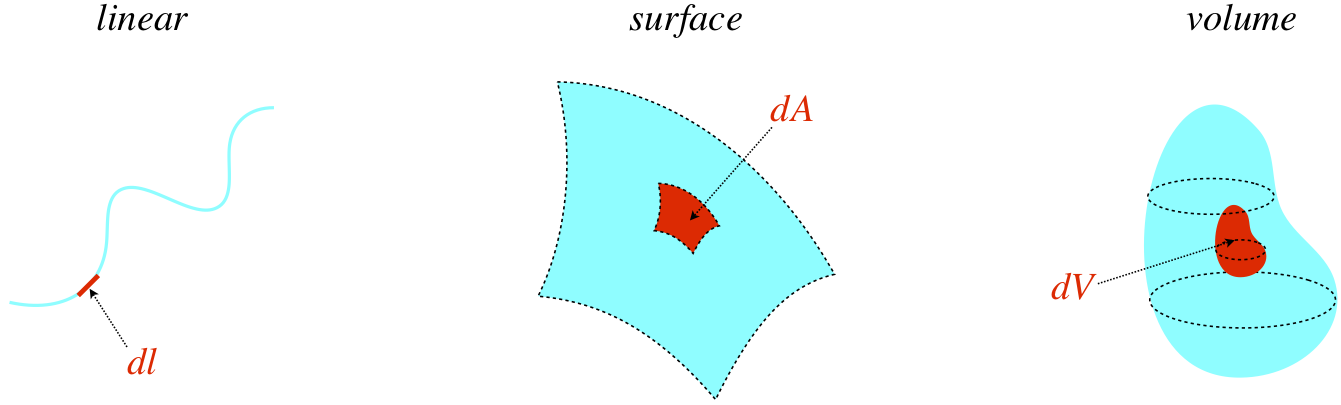
The small (infinitesimal) bit of charge residing in each of these regions is found by multiplying the density (located at the position of that region – the density doesn't have to be the same everywhere!) by the size of the region. Typically linear charge densities are represented by a \(\lambda\), surface charge densities by a \(\sigma\), and volume charge densities by a \(\rho\):
\[dq = \lambda \; dl \;\;\;\;\;\;\;\;\;\; dq = \sigma\;dA \;\;\;\;\;\;\;\;\;\; dq = \rho\;dV \]
Alert
The charge \(dq\) has units of coulombs in every case, which means that these three types of density all have different units: \(Cm^{-1}\), \(Cm^{-2}\), and \(Cm^{-3}\), respectively.
If we want to know the total amount of charge along a line, on a surface, or within a volume, then we need to integrate these infinitesimal amounts over the full region. Again, the densities are not necessarily uniform, so the density is a function of position, and cannot be removed from the integral:
\[Q_{tot} = \int\limits_{whole\;line} \lambda\;dl \;\;\;\;\;\;\;\;\;\; Q_{tot} = \int\limits_{whole\;surface} \sigma\;dA \;\;\;\;\;\;\;\;\;\; Q_{tot} = \int\limits_{whole\;volume} \rho\;dV \]
When it comes to using continuous charge distributions to compute electric fields, there is one critical idea that comes into play:
An infinitesimal chunk of charge is so small that its field is precisely that of a point charge, so we can write it as a coulomb field.
So the idea of computing the electric field of a continuous distribution of charge is to write down the (coulomb) electric field of a single infinitesimal chunk, and then add up (integrate) the electric field contributions of all the chunks.
Alert
We have to keep in mind that the electric field contributions are vectors, which adds a layer of complication to the problem. The right approach is to compute the components of the field vector separately. Fortunately, there are often tricks related to symmetry we can use to simplify this particular step.
The secret to solving such problems is to proceed slowly and methodically. We will break down the steps here with a simple example of a 1-dimensional charge distribution.
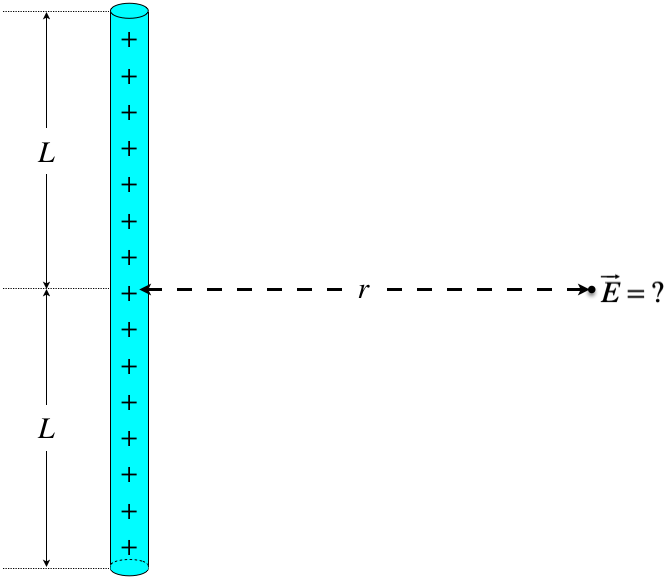
Electric Field of a Straight Line Segment of Uniform Density
Our line segment will have a length of \(2L\), a total charge of \(Q\), and we will be computing the field at a position a perpendicular distance \(r\) from the center of the line segment. We'll treat the charge as if it is positive. If we want the solution for a negative charge, we just have to flip the direction of the electric field.
Figure 1.3.2a – Field of a Uniform Line Segment
Step 1: Sketch an arbitrary infinitesimal chunk of charge, and its contribution to the field vector.
Figure 1.3.2b – Field of a Uniform Line Segment
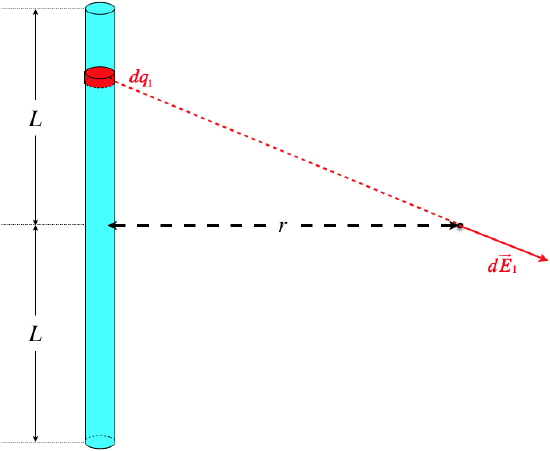
Step 2: Break the field vector into appropriate components and make a symmetry argument (if applicable).
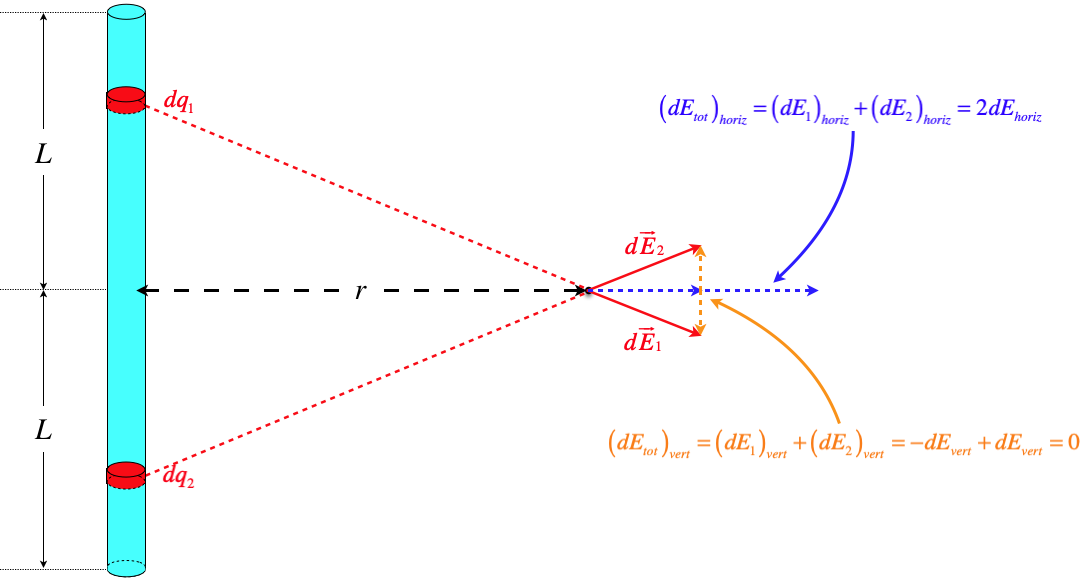
This step requires a bit of clarification. Our integral will be adding field contributions for every little chunk of charge in the line segment, but we have to add these as vectors. The simplest way to do this is to add like components. In this case, the electric field of every chunk will generally have a vertical and horizontal component (within the plane of the page). We will therefore need to do two integrals – one that adds up the vertical electric field components, and one that adds up the horizontal components.
Notice that for every chunk above the center line, there is another corresponding chunk below it. These "twin" chunks will provide horizontal components to the field that are equal and in the same direction, but the vertical components, while equal in magnitude, oppose each other. When we add up the vertical components over the entire line segment, we therefore find that they cancel, meaning we know (without performing an integral) that the electric field has zero vertical component.
Alert
This symmetry only applies to points on the line perpendicular to the center of the line segment, and only because the charge distribution is uniform. Fortunately, that is what we are calculating here.
Figure 1.3.2c – Field of a Uniform Line Segment
Step 3: Introduce a coordinate system and label everything.
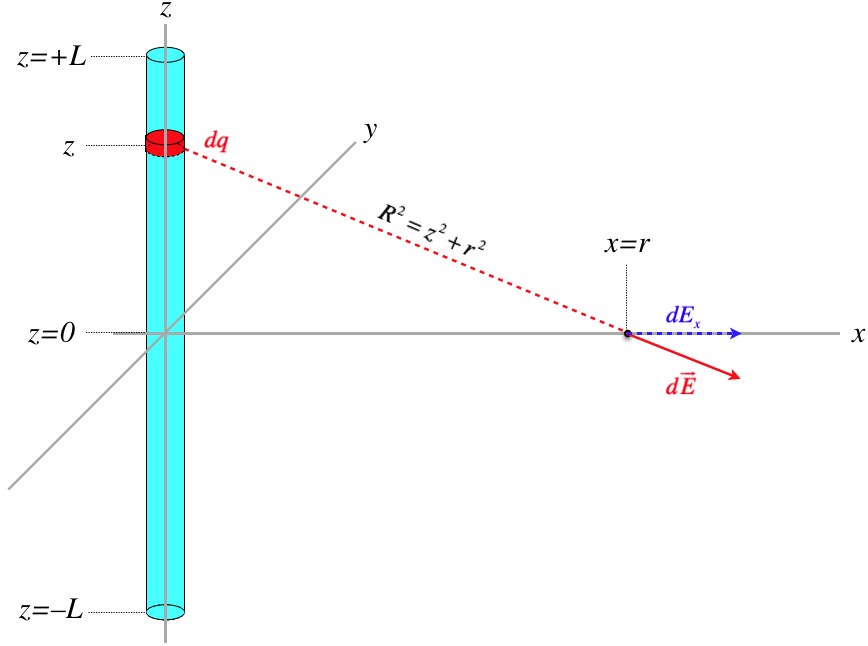
Don't be afraid to introduce variables! Ultimately the answer needs to be in terms of what has been given (in this case, that would be \(L\), \(Q\), and \(r\)), but since you can't simply write down the answer, you need to create some variables to work with. Besides the coordinate axes, we introduce the variable \(R\) to represent the distance separating a chunk of charge from the position of the field, and the angle \(\theta\) to allow us to express the horizontal component of the field. Note that the \(y-\)axis in the diagram below is not necessary, as it is clear that the field will not have a \(y-\)component in the coordinate system shown.
Figure 1.3.2d – Field of a Uniform Line Segment
Step 4: Relate the differential chunk of charge to the charge density, using the coordinate system.
This is a linear distribution and the length of the chunk expressed in terms of the coordinate system is \(dz\), so we have:
\[dq = \lambda \; dz\]
But we also know that the charge density is uniform, so it is the ratio of the total charge and the total length:
\[\lambda = \dfrac{Q}{2L} \;\;\; \Rightarrow \;\;\; dq = \dfrac{Q}{2L} \; dz \]
Step 5: Apply the fact that an infinitesimal chunk acts like a point charge to produce an infinitesimal coulomb field.
We have called the distance from the chunk to the point of the field \(R\), so:
\[ dE = \dfrac{k\;dq}{R^2} = \dfrac{kQ}{2L}\left[\dfrac{dz}{z^2+r^2}\right] \]
Step 6: Construct the component of the field from the magnitude, and convert variables into the integration variable.
We can't just integrate \(dE\) at this point! We are adding the horizontal components, not the magnitudes. With our definition of \(\theta\), we have:
\[ dE_x = dE\cos\theta = \dfrac{kQ}{2L}\left[\dfrac{dz}{z^2+r^2}\right]\cos\theta \]
We still can't integrate yet, because as we start accounting for different chunks (i.e. integrate over \(z\)), the value of \(\theta\) changes. We therefore need to write \(\theta\) in terms of \(z\). Fortunately, we have a nice right triangle to work with:
\[\cos\theta = \dfrac{r}{R} = \dfrac{r}{\sqrt{z^2+r^2}} \;\;\; \Rightarrow \;\;\; dE_x =\dfrac{kQr}{2L}\left[\dfrac{dz}{\left(z^2+r^2\right)^{\frac{3}{2}}}\right] \]
Step 7: Integrate over all of the chunks of electric charge.
In this case, the chunks lie from \(z=-L\) to \(z=+L\). We already noted that symmetry demands that the contributions of the lower half will be the the same as those of the upper half. We can see that this will be the case by replacing \(z\) in the integrand with \(-z\) – the same integral results. If we like, we can change the limits to \(0\rightarrow +L\) and multiply the integral by 2:
\[ E_x = 2\int\limits_0^L \dfrac{kQr}{2L}\left[\dfrac{dz}{\left(z^2+r^2\right)^{\frac{3}{2}}}\right] \]
Perhaps your palms are getting sweaty at this point, with the thought of now having to perform an integral like this. Well, first of all, it isn't that bad. But even if it was, we will be more focused on the physics of these problems than proficiency with techniques of integration, so we will liberally use integral tables to look these up once we have constructed them. This is not to say that you never have to do any math, of course. It's not always obvious how the integral you have can be placed in the form given in an integral table, so you are expected to make substitutions or do whatever it takes to make the integral tables actually useful to you. Anyway, this particular integral comes out to be (check it by taking a derivative!):
\[ E_x = \dfrac{kQr}{L}\left[\dfrac{z}{r^2\sqrt{z^2+r^2}}\right]_0^L = \dfrac{kQ}{r\sqrt{L^2+r^2}} \;\;\; \Rightarrow \;\;\; \overrightarrow E\left(r\right) = \dfrac{kQ}{r\sqrt{L^2+r^2}} \widehat r\]
Notice that after the integral is performed, all of the variables we introduced are gone (the last one to vanish being the integration variable).
We already concluded that the \(y\) and \(z\) components of the field vanish at this point. The \(y\) component is zero because we defined the coordinate system so that this would be true. If we were to treat this more generally, we would note that no matter how we set up the \(x\) and \(y\) axes, the electric field points directly away from the segment (axially outward for a line of positive charge), which is why we have used the unit vector \(\widehat r\) instead of the unit vector along the \(x\)-axis only.
The \(z\) component is zero because of symmetry, but if we hadn't noticed this shortcut, we could still have concluded this. Going back to step 5, we would compute:
\[ dE_z = dE\sin\theta = \dfrac{kQ}{2L}\left[\dfrac{dz}{z^2+r^2}\right]\sin\theta \]
Using our right triangle to substitute for \(\sin\theta\), we get a \(z\) in the numerator instead of the \(r\) that we got last time:
\[ dE_z =\dfrac{kQ}{2L}\left[\dfrac{zdz}{\left(z^2+r^2\right)^{\frac{3}{2}}}\right] \]
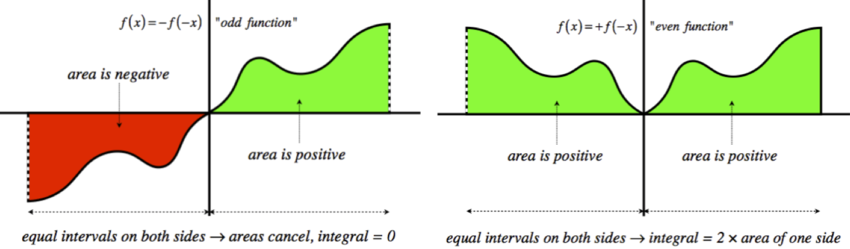
This integral differs from the previous one by a factor of \(z\), which makes all the difference. Once again, the limits of integration are symmetric about the origin, but now if we replace \(z\) in the integrand with \(-z\), we get the negative of the original integral. When these are added together for the two halves of the integral, we get zero. This is a nice mathematical trick you can use in these situations that avoids the need to do integrals like this one that come out to zero. If the integral is being performed over an interval over which the integrand is “odd” about the center of that interval (I will define “odd/even” in this context in a moment), then the integral comes out to be zero. If the integrand is “even,” then the integral is double the value of the integral over half the interval. The integrand above is an odd function of \(z\), meaning the function changes sign when \(z\rightarrow -z\). The limits of integration are symmetric across the origin, so this fits the bill for a zero integral as described.
Figure 1.3.3 – Integrating Odd vs. Even Functions
Example \(\PageIndex{1}\)
A thin circular plastic ring with a radius of \(a\) carries a net charge \(Q\) that is uniformly distributed throughout. For a common point of reference, we will place this ring in the \(yz\) plane, centered at the origin. Find the electric field at all points on the \(x\)-axis.
- Solution
-
First a diagram, to label the needed variables:
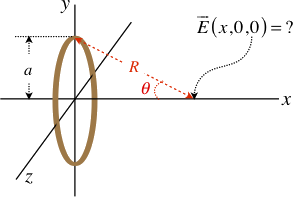
The distance from a small segment of the circle to the point \(x\) is:
\[ R=\sqrt{a^2+x^2} \nonumber \]
So the small contribution to the magnitude of the electric field by this element is:
\[dE=\dfrac{k\;dq}{a^2+x^2} \nonumber \]
Thanks to the symmetry of the circle, the \(y\) and \(z\) components of this electric field all cancel out (for every element on the ring there is an element on the opposite side that cancels the components that are not in the \(x-\)direction). So the only part of the electric field we can keep is the \(x-\)component, which we find by multiplying the magnitude by the cosine of the angle \(\theta\) shown in the diagram. This cosine can be written in terms of the right triangle shown above:
\[dE_x = dE\cos\theta = \left(\dfrac{k\;dq}{a^2+x^2}\right)\left(\dfrac{x}{R}\right) = \dfrac{kx\;dq}{\left(a^2+x^2\right)^{\frac{3}{2}}} \nonumber \]
Now all we have to do is add up all of the \(dq\) contributions. The amount of charge in an infinitesimal segment of the circle (which is given by the radius times the infinitesimal angle the segment subtends) in terms of the linear charge density \(\lambda\) is:
\[dq = \lambda \left(a\;d\phi\right) \nonumber \]
Because the charge density is uniform, it is simply equal to the total charge divided by the length, which is the circumference of the loop:
\[\lambda = \dfrac{Q}{2\pi a} \;\;\;\Rightarrow\;\;\; dq = \dfrac{Q}{2\pi} d\phi \nonumber\]
Plugging this in and integrating around the entire ring (\(\phi\) ranges from 0 to \(2\pi\), and \(x\) remains constant throughout the integral) gives the answer:
\[E_x = \dfrac{Q}{2\pi}\dfrac{kx}{\left(a^2+x^2\right)^{\frac{3}{2}}}\int\limits_0^{2\pi} d\phi = \dfrac{kQx}{\left(a^2+x^2\right)^{\frac{3}{2}}} \nonumber \]
This is just the \(x-\)component of the field, but since the other components vanish, we have that the field vector on the axis at point \(x\) is:
\[\overrightarrow E\left(x,0,0\right) = \dfrac{kQx}{\left(a^2+x^2\right)^{\frac{3}{2}}} \widehat i \nonumber\]
Note that the direction changes when \(x\) is negative, as it should. Also note that the electric field vanishes at the origin and at infinity, as we would expect.
Electric Field of a Circular Disk of Uniform Density
We next take on a problem that differs from the previous one in two ways. First, it involves a two-dimensional charge distribution (which requires a double integral), and second, we will need to use polar coordinates rather than cartesian. Despite the differences, however, the steps we take are the same.
Our disk will have a radius of \(a\), a total charge of \(Q\), and we will be computing the field at a position a perpendicular distance \(l\) from the center of the disk.
Figure 1.3.4a – Field of a Uniform Disk
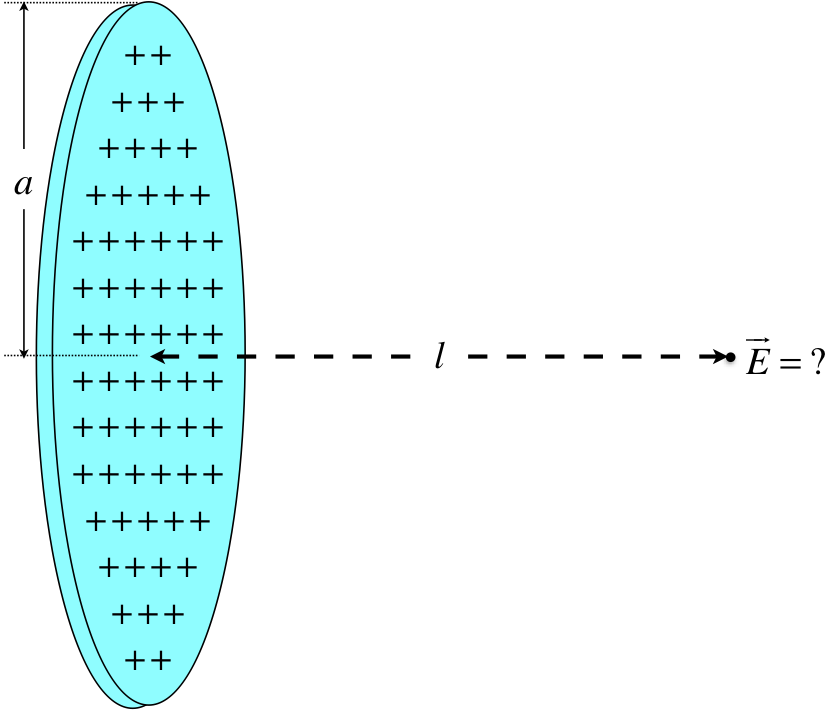
Step 1: Sketch an arbitrary infinitesimal chunk of charge, and its contribution to the field vector.
This is a bit trickier than before, because the chunk is not a simple line segment, and we have to keep an eye on what we will be integrating later. For example, we could draw a chunk that is a square, but integrating this in cartesian coordinates would be challenging. So instead, we choose an arc with a radial thickness.
Figure 1.3.4b – Field of a Uniform Disk
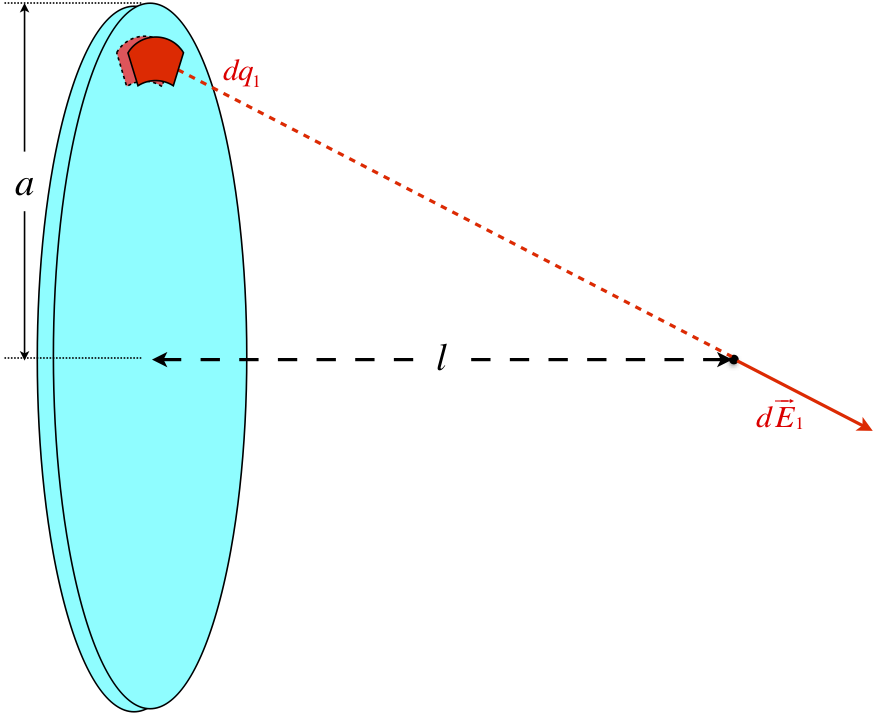
Step 2: Break the field vector into appropriate components and make a symmetry argument (if applicable).
As before, we find that there is symmetry (this time, axial) which creates opposing contributions to the electric field vector along directions perpendicular to the central axis.
Figure 1.3.4c – Field of a Uniform Disk
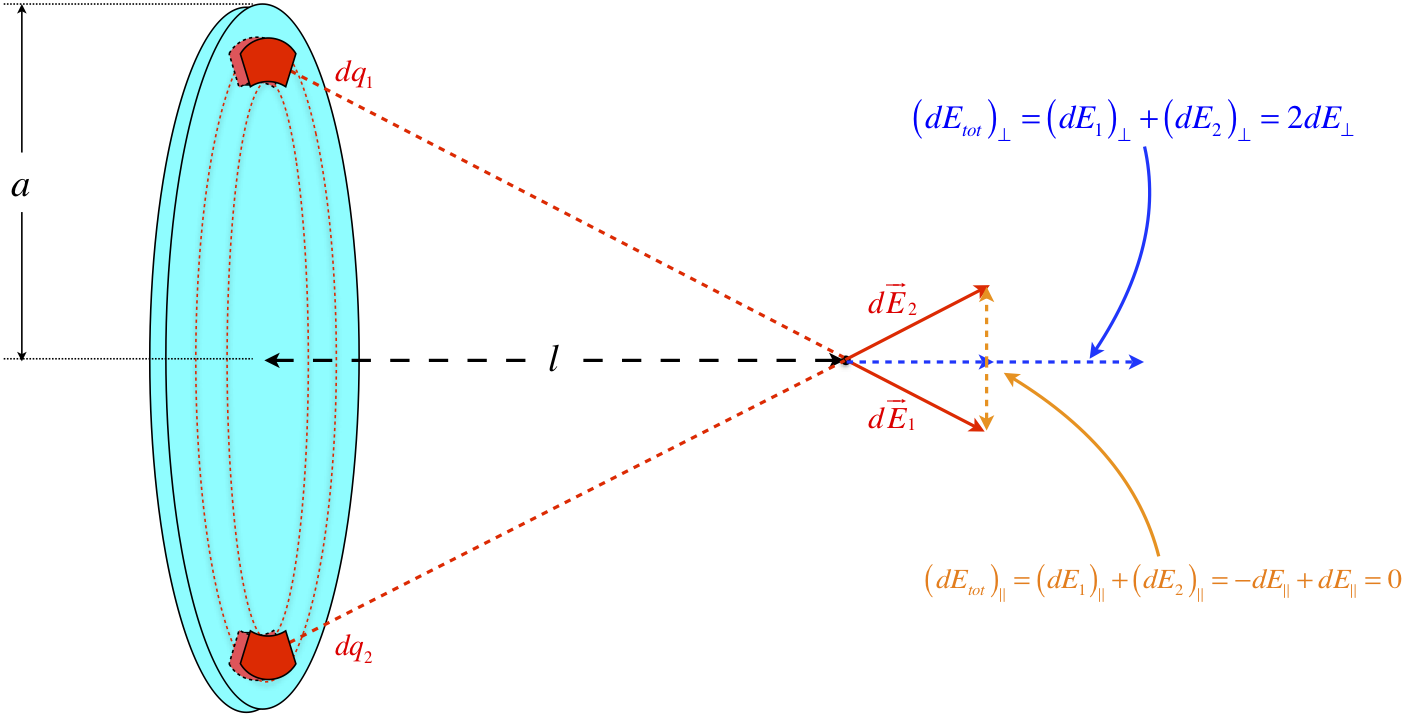
Step 3: Introduce a coordinate system and label everything.
The shape of our collection of charge calls for a use of polar coordinates to describe the position of the chunks of charge.
Figure 1.3.4d – Field of a Uniform Disk
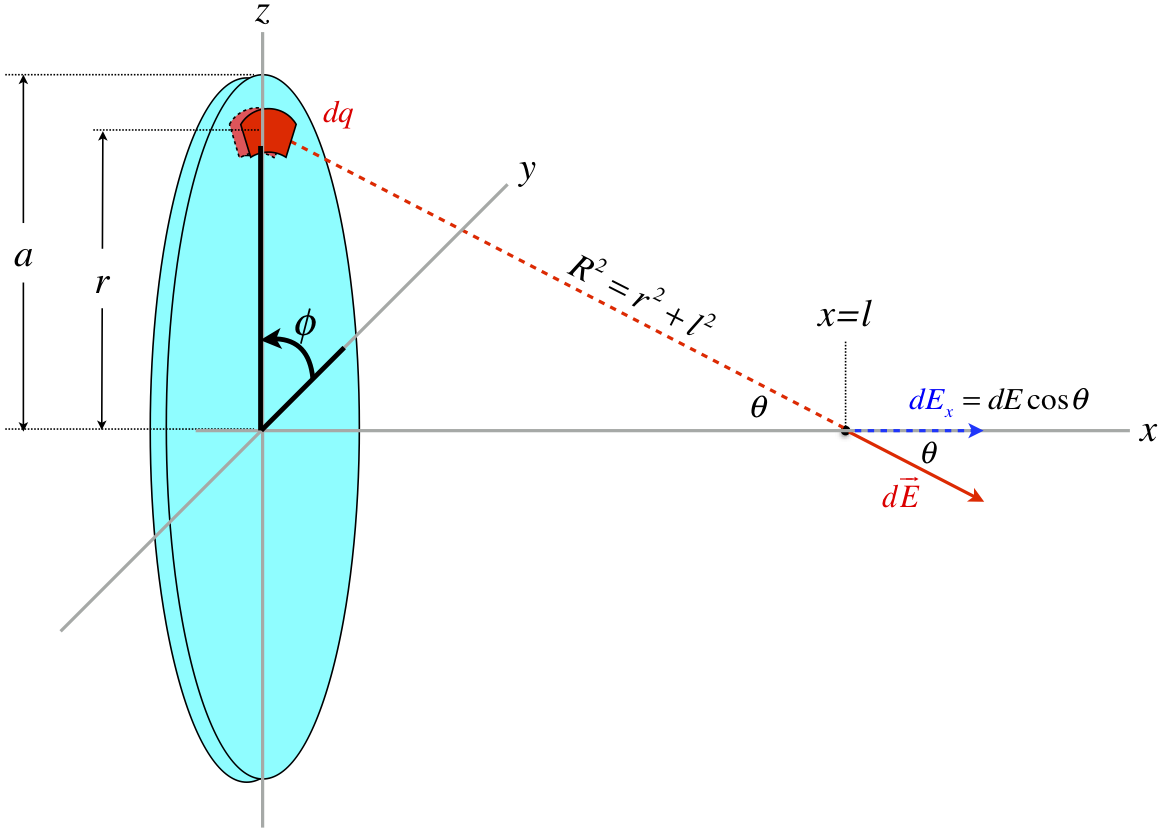
Step 4: Relate the differential chunk of charge to the charge density, using the coordinate system.
This is a surface charge density, so we need to multiply the constant charge density by the infinitesimal area of the chunk in order to get \(dq\). Since we are using polar coordinates, this requires a closer look at the geometry of the chunk:
Figure 1.3.4e – Field of a Uniform Disk
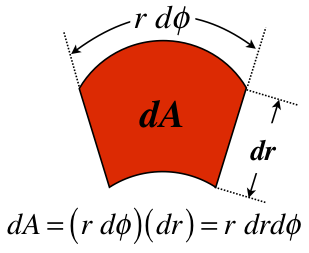
The infinitesimal charge in terms of the charge density is therefore:
\[ dq = \sigma\;dA = \sigma r dr d\phi \]
The charge density is uniform, which means that the total charge is the density multiplied by the total area of the disk, which gives:
\[ \sigma = \dfrac{Q}{\pi a^2} \;\;\; \Rightarrow \;\;\; dq = \dfrac{Q}{\pi a^2}r \;dr \;d\phi \]
Step 5: Apply the fact that an infinitesimal chunk acts like a point charge to produce an infinitesimal coulomb field.
\[ dE = \dfrac{k\;dq}{R^2} = \dfrac{kQ}{\pi a^2}\left[\dfrac{r \;dr \; d\phi}{r^2+l^2}\right] \]
Step 6: Construct the component of the field from the magnitude, and convert variables into the integration variable.
\[ dE_x = dE\cos\theta = \dfrac{kQ}{\pi a^2}\left[\dfrac{r \;dr \; d\phi}{r^2+l^2}\right]\cos\theta = \dfrac{kQ}{\pi a^2}\left[\dfrac{r \;dr \; d\phi}{r^2+l^2}\right]\left[\dfrac{l}{R}\right] = \dfrac{kQl}{\pi a^2}\dfrac{r \;dr \; d\phi}{\left(r^2+l^2\right)^{\frac{3}{2}}} \]
Step 7: Integrate over all of the chunks of electric charge.
To include the contributions of all the chunks, we integrate the angle around the entire circle (\(\phi=0\rightarrow 2\pi\)), and the radius from the center out to the edge (\(r=0\rightarrow a\)). Notice that integrating around the whole circle and from the center to the radius takes care of the "opposing" chunks everywhere around the disk – the components of the field perpendicular to the axis cancel, and those parallel all add (no need to multiply by 2, as we did when we integrated from the center of the line of charge earlier, to include both sides).
\[ E_x = \dfrac{kQl}{\pi a^2}\int\limits_0^{2\pi} d\phi \int\limits_0^{a} \dfrac{r\;dr}{\left(r^2+l^2\right)^{\frac{3}{2}}} \]
The integral over \(d\phi\) is simply equal to \(2\pi\), and the integral over \(r\) is so common that we shouldn't even have to look it up (though it is fine to do so). Make the substitution \(u\equiv \left(r^2+l^2\right)^{-\frac{1}{2}}\) and the integral comes out immediately:
\[ E_x =\dfrac{kQl}{\pi a^2}\left(2\pi\right)\left[\dfrac{-1}{\sqrt{r^2+l^2}}\right]_{r=0}^{r=a} \;\;\;\Rightarrow \;\;\; \overrightarrow E\left(l,0,0\right) = \dfrac{2kQ}{a^2}\left(1-\dfrac{l}{\sqrt{a^2+l^2}}\right) \widehat i \]
Example \(\PageIndex{2}\)
A thin, hollow, plastic cylinder with a radius of \(a\) and length \(2L\) carries a net charge \(Q\) that is uniformly distributed throughout. For a common point of reference, we will place this cylinder with its axis along the \(z\)-axis, centered at the origin (see the diagram). Find the electric field at all points on the \(z\)-axis.
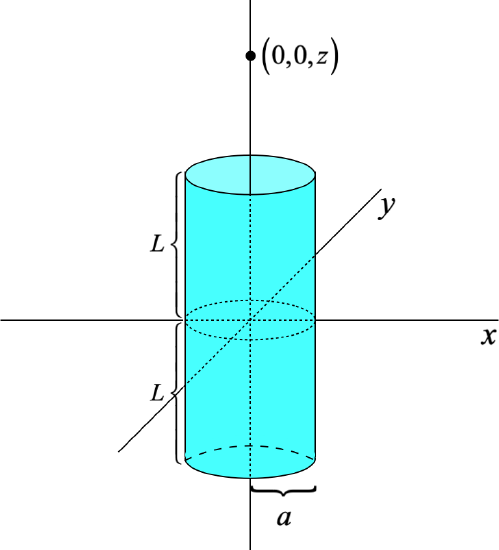
- Solution
-
Every infinitesimal piece of this cylinder behaves like a point charge, and we need to add the contributions of those point charges to the electric field. So we start by diagramming an arbitrary element of charge as a small patch of area on the cylinder:
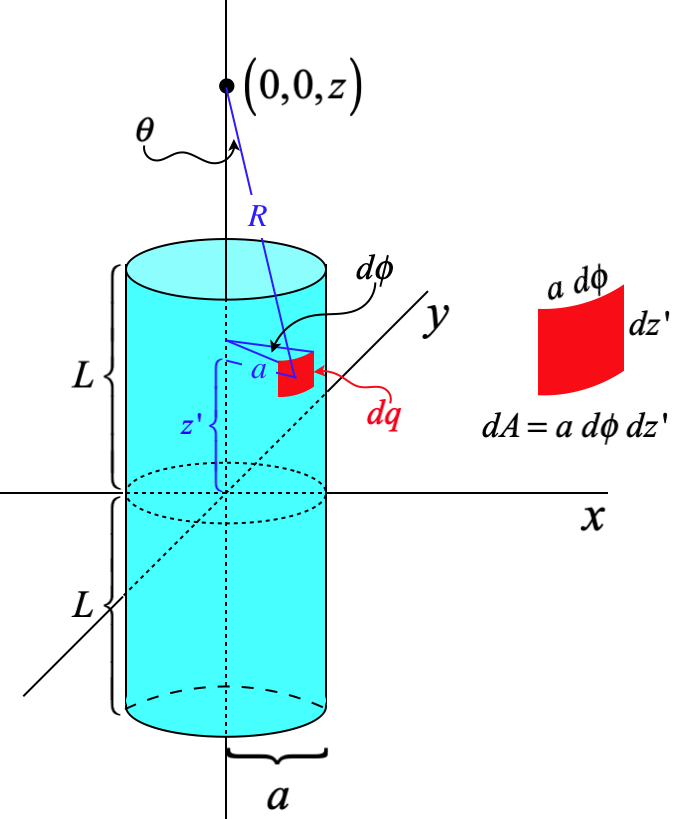
The infinitesimal patch of charge has an area that equals its height \(dz'\) multiplied by its arclength \(ad\phi\), as indicated in the diagram.
[Note that the \(z\)-position of the patch (and its infinitesimal length in the \(z\)-direction) are labeled with a prime (\(z'\)). This is because we will be adding up the contributions of all the patches, which entails integrating over that variable, and we need to distinguish that quantity from the value \(z\) that describes the position where we are measuring the electric field.]
To calculate the electric field requires calculating all three components separately, but we find once again that two of the components (\(E_x\) and \(E_y\) vanish thanks to the symmetry we have by considering only points on the \(z\)-axis. We therefore only calculate the \(z\) component contributed by every charge element, which, in terms of the electric field magnitude of the charge element is:
\[dE_z = dE\cos\theta = dE\left(\dfrac{side\;adjacent}{hypothenuse}\right)= dE\left(\dfrac{z-z'}{R}\right)\nonumber\]
Now we write down the coulomb field for the point charge, once again writing the charge element in terms of the constant surface density, which we will call \(\sigma\):
\[dE=\dfrac{kdq}{R^2} = \dfrac{k\sigma dA}{R^2} = \dfrac{k\sigma a\;d\phi dz'}{R^2}\nonumber\]
The charge density is uniform, so it is simply the total charge divided by the total surface area of the cylinder:
\[\sigma = \dfrac{Q}{2\pi a \left(2L\right)} = \dfrac{Q}{4\pi aL}\]
Putting together everything we have so far gives:
\[dE_z = \dfrac{kQ\left(z-z'\right)}{4\pi LR^3}d\phi dz'\nonumber\]
We are going to have to integrate over the entire surface of the cylinder, so we need to integrate over the variables \(z'\) and \(\phi\). No part of the integrand depends upon \(\phi\), and the limits of integration for that variable are \(0\rightarrow 2\pi\). The quantity \(R\) depends upon \(z'\), which we can express using the pythagorean theorem. The limits for the integration over \(z'\) are \(-L\rightarrow +L\), so we are left with:
\[E_z = \dfrac{kQ}{4\pi L} \int\limits_{0}^{2\pi}d\phi \int\limits_{-L}^{+L}\dfrac{z-z'}{\left[a^2+\left(z-z'\right)^2\right]^{\frac{3}{2}}}dz'\nonumber\]
The integral over \(\phi\) is trivial, and the second integral is pretty straightforward with the substitution \(u\equiv z-z'\):
\[E_z = \dfrac{kQ}{2L}\int\limits_{z+L}^{z-L}\dfrac{-u}{\left[a^2+u^2\right]^{\frac{3}{2}}}du = \dfrac{kQ}{2L}\left[\dfrac{1}{\sqrt{a^2+u^2}}\right]_{z+L}^{z-L} = \dfrac{kQ}{2L}\left[\dfrac{1}{\sqrt{a^2+\left(z-L\right)^2}}-\dfrac{1}{\sqrt{a^2+\left(z+L\right)^2}}\right]\nonumber\]
Example \(\PageIndex{3}\)
Show that the solutions to the two previous examples are consistent with each other, by noting that a thin ring is equivalent to a very hollow cylinder with a very short length.
- Solution
-
We could get the solution to Example 1.3.1 by taking the limit of the solution to Example 1.3.2 as the length of the cylinder goes to zero:
\[\lim\limits_{L\rightarrow 0} E_z = \dfrac{kQ}{2\cdot 0}\left[\dfrac{1}{\sqrt{a^2+z^2}}-\dfrac{1}{\sqrt{a^2+z^2}}\right] = \dfrac{0}{0}\nonumber\]
We get an indeterminate form, which means we need to use l'Hôpital's rule:
\[\begin{array}{l} \lim\limits_{L\rightarrow 0} E_z && = && \dfrac{kQ}{2} \lim\limits_{L\rightarrow 0} \dfrac{\dfrac{d}{dL}\left[\dfrac{1}{\sqrt{a^2+\left(z-L\right)^2}}-\dfrac{1}{\sqrt{a^2+\left(z+L\right)^2}}\right]}{\dfrac{d}{dL}L} \\ && = && \dfrac{kQ}{2} \lim\limits_{L\rightarrow 0} \left[\dfrac{z-L}{\left[a^2+\left(z-L\right)^2\right]^{\frac{3}{2}}} + \dfrac{z+L}{\left[a^2+\left(z+L\right)^2\right]^{\frac{3}{2}}}\right] \\ && = && \dfrac{kQz}{\left(a^2+z^2\right)^{\frac{3}{2}}} \end{array}\nonumber\]
This is the same result as in Example 1.3.1, where, of course, we have swapped the \(x\)-axis for the \(z\)-axis.
Infinite Lines and Planes of Charge
A particularly useful aspect of the solutions provided above for the line segment and the disk lies in extending the result to charge distributions that are infinite in extent. To see how to make this extension, we first need to change the form of the solutions so that they reflect the charge density, rather than the total charge:
\[\overrightarrow E_{line\;segment}\left(r\right) = \dfrac{kQ}{r\sqrt{L^2+r^2}} \widehat r = \dfrac{2kL\lambda}{r\sqrt{L^2+r^2}} \widehat r \]
\[\overrightarrow E_{disk}\left(x\right) = \dfrac{2kQ}{a^2}\left(1-\dfrac{x}{\sqrt{a^2+x^2}}\right) \widehat i = 2\pi k \sigma\left(1-\dfrac{x}{\sqrt{a^2+x^2}}\right) \widehat i \]
For both cases, we can extend the solution to the infinite cases by letting the parameter \(a\) go to infinity.
The solutions for the infinite line and plane take on significantly simpler forms than for the finite cases. But there is another simplification for these cases as well: In the finite cases, we had to be careful to remember that the solutions only applied along the point of symmetry, equally-spaced between the extremes of the charge distributions (i.e. in the \(xy\) plane for the line segment, and on the \(x-\)axis for the disk). But with these distributions now having infinite extent, everywhere represents a symmetric position, so these solutions are good everywhere in space.
It might seem strange that the electric field is uniform everywhere in space for the infinite plane. Why doesn't the field get stronger closer to the plane of charge? This can be more easily seen using the field line description. If the field got stronger closer to the plane, then the field lines would have to get closer together there. But that can only happen if the field lines are not perpendicular to the plane everywhere. Due to the symmetry of the infinite plane, there is no reason to believe that the field would have any \(y\) or \(z\) components anywhere in space. With the field only pointing along the \(x\) direction, the field lines can't change their separation, and the field strength remains constant everywhere.
One might ask that although these solutions have simpler forms, how can they be "useful," as claimed above? How many infinite lines or planes of charge does one run across in real life? The answer is that all solutions in physics are approximations, and are only useful up to the sensitivity of the measurements. For example, if we look at the field of a finite-sized plane of charge, but look at a position in space that is very close to the plane compared to the dimensions of that plane, then treating it as "infinite" is a good approximation. What is especially nice about this approximation is that so long as we are looking at positions close to the plane compared to the distance from the edges, we don't even care what shape the plane is – it can be a circular disk, a square, or some random, jagged shape.
One other comment about usefulness. Once we have made a computation, we don't have to do it over again. That means that to the extent that a new problem has elements that can be approximated as these above, we can simply use the solutions – we don't have to start from scratch and perform an integral every time. We saw this utility once before in Physics 9A, where we may have performed an integral to compute the moment of inertia of a rod or some other object, but after that, we can just use what we computed.
Non-Uniform Charge Distributions
So far all we have considered are charge distributions that are uniform. These cases involve two simplifications. The first is that the physical situation is more likely to include a symmetry that simplifies the calculation of the field. For example, if the case of the line segment of charge solved above did not include a uniform charge density, then the electric field on the \(x\)-axis may not have a vanishing \(z\)-component. Second, the relationship between the charge and charge density is different, which puts another function into the integral. Despite these differences, there are still cases for which symmetry is still a useful tool, and the overall approach is exactly the same as has been shown above.
Example \(\PageIndex{4}\)
A positively-charged thin plastic rod of length \(L\) is placed on the \(+x\)-axis with one end at the origin. The linear distribution of charge on this rod satisfies the equation:
\[\lambda\left(x\right) = \lambda_o\dfrac{x^2}{L^2}\nonumber\]
A point particle with the same charge as the rod is also placed somewhere on the \(-x\)-axis, and the resulting total electric field at the origin vanishes.
- Find the charge of the point particle (in terms of the given quantities \(L\) and \(\lambda_o\)).
- Find the position of the point particle.
- Solution
-
a. The point particle has the same total charge as the rod, so we need to compute the charge on the rod given the density function. Unlike cases of uniform linear charge distributions where the total charge is simply the product of the density and the length, in this case, we need to add up all the small contributions:
\[Q=\int dq = \int \lambda\left(x\right)dx = \int_0^L \lambda_o\dfrac{x^2}{L^2}dx = \lambda_o\left[\dfrac{x^3}{3L^2}\right]_0^L = \frac{1}{3}\lambda_oL \nonumber\]
b. Now we need to compute the electric field due to the rod in terms of the charge, and then we can determine the position of the point particle that will cancel that field. We start with a diagram:
The amount of charge contained in the infinitesimal slice is, as we used above:
\[dq = \lambda dx = \lambda_o\dfrac{x^2}{L^2}dx \nonumber\]
There is no need to worry about components of the electric field here, as it clearly only has an \(x\)-component at the origin. Calling the position of the tiny bit of charge \(x\), the field at the origin due to \(dq\) is the usual coulomb field, giving:
\[dE = \dfrac{kdq}{x^2}=\dfrac{k\left[\lambda_o\dfrac{x^2}{L^2}dx\right]}{x^2}\;\;\; \Rightarrow \;\;\; E=\dfrac{k\lambda_o}{L^2}\int_0^L dx = \dfrac{k\lambda_o}{L}\nonumber\]
We need this field in terms of the total charge, so we can use the result of part (a) to substitute for \(\lambda_o\):
\[\lambda_o = \dfrac{3Q}{L} \;\;\; \Rightarrow \;\;\; E=\dfrac{3kQ}{L^2}\nonumber\]
The electric field of the point particle must have this same magnitude at the origin, so calling its distance from the origin \(r\) we find:
\[\dfrac{kQ}{r^2}=\dfrac{3kQ}{L^2}\;\;\; \Rightarrow \;\;\; r=\dfrac{L}{\sqrt 3} \nonumber\]
Some General Comments
Now for a few general observations about this process of computing the electric field…
- The sub-steps become tougher as the geometry becomes more complex. Here are a few of these problem spots:
- Labeling the position of the source point charge is a bit trickier if it lies within a 2-dimensional plane (or within a 3-dimensional volume), rather than on a 1-dimensional line. For example, for a surface of charge that is a circle or a cylinder, you could use rectangular coordinates, but then the limits of integration get significantly tougher. In general, the symmetry of the physical situation will dictate what is the best coordinate system to use.
- The element of charge written in terms of the coordinates is more complicated. Typically we just choose an appropriate coordinate system and look up the expression for an infinitesimal element of length/area/volume (see below for references), but that doesn’t mean it’s easy.
- For surfaces, there are two variables over which we must integrate (for volumes, where we will not venture, there are three). If we choose a good coordinate system, symmetry usually means that we have only one non-trivial integral. Also, we could choose an element that allows for a shortcut (such as that which we used in Example 1.3.3), but that gets away from the notion of superposing the fields of many point \(dq\) charges, which can confuse our understanding of the situation on physical grounds.
- We have relied heavily upon symmetry to avoid doing calculations of many of the components that vanish, but one needs to be aware that in general solving for the electric field involves three solutions – one for each component – all performed in the same manner. It is a good exercise to go back to the examples above and show that the zero components are indeed zero without resorting to symmetry arguments. If the reader cannot manage this, then that is an indication of a shortcoming in understanding how such calculations are performed.
- While every case shown above involves finding the field outside the charge distribution, there is also an electric field within the distribution, calculated exactly the same way.
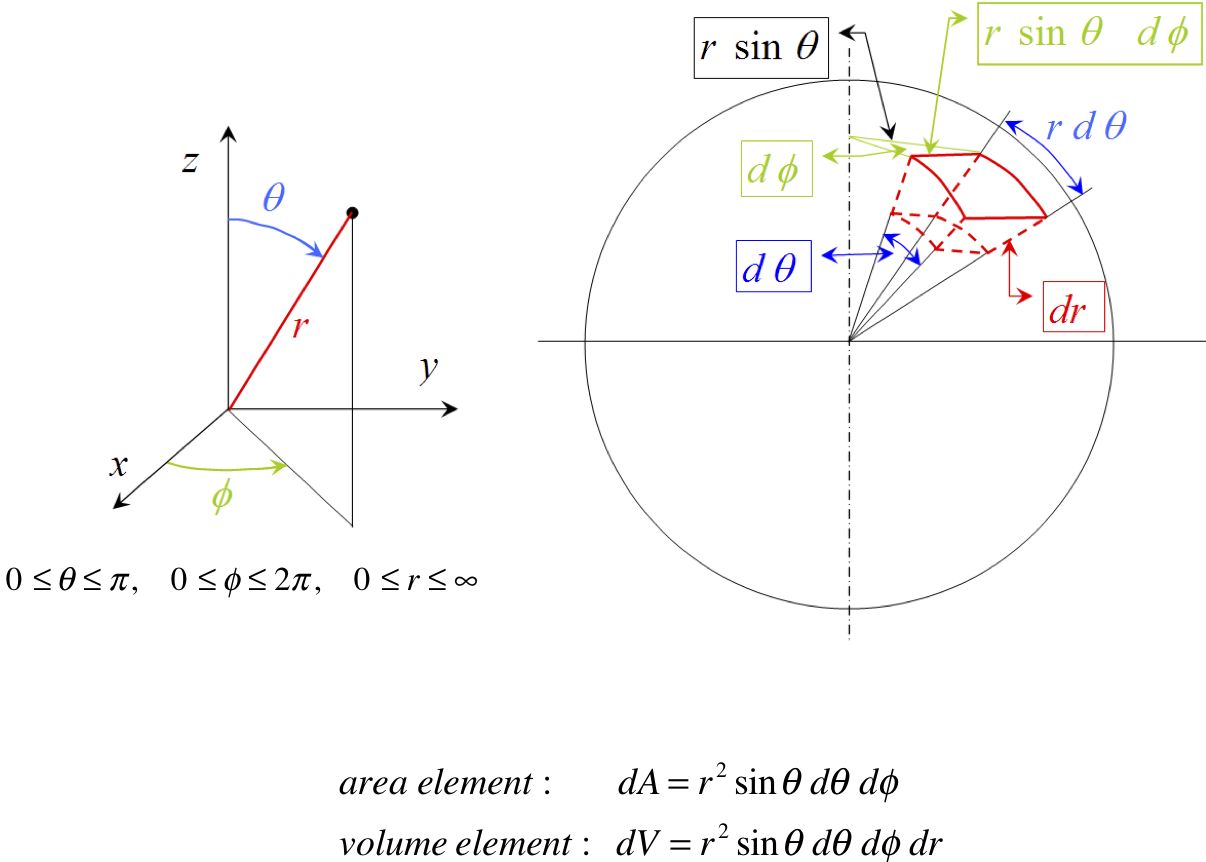
Area and Volume Elements
For reference purposes, we present here the area and volume elements for cartesian, cylindrical, and spherical coordinates.
Figure 1.35 – Cartesian Coordinates
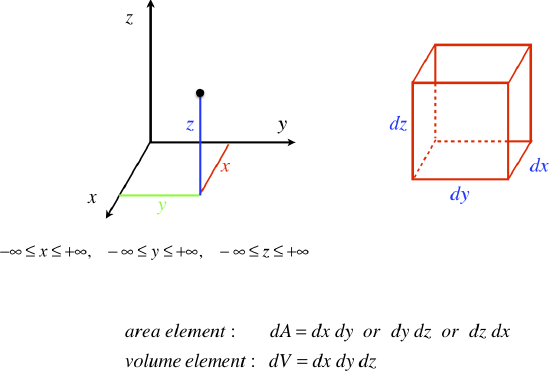
Figure 1.36 – Cylindrical Coordinates
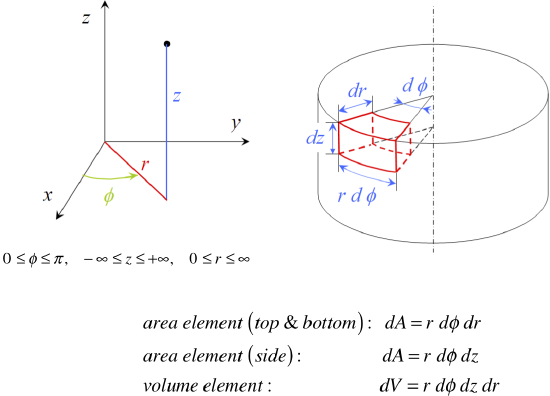
Figure 1.37 – Spherical Coordinates