3.2: Conservative and Non-Conservative Forces

Gravity is a Conservative Force

Let’s take a closer look at the work contributions by some of the various forces we have discussed. We’ll start with gravity. In our earlier examples of a loop-de-loop and a pendulum, we saw that the contact and tension forces didn’t contribute to work on the object, but what about gravity? Yes, of course it does work, because in both cases, for much of the journey, the gravity force on the object was not perpendicular to its motion. We’ll look at these cases again, but first let’s consider the work done by gravity on a projectile.

Figure 3.2.1 – Work Done on Projectile by Gravity

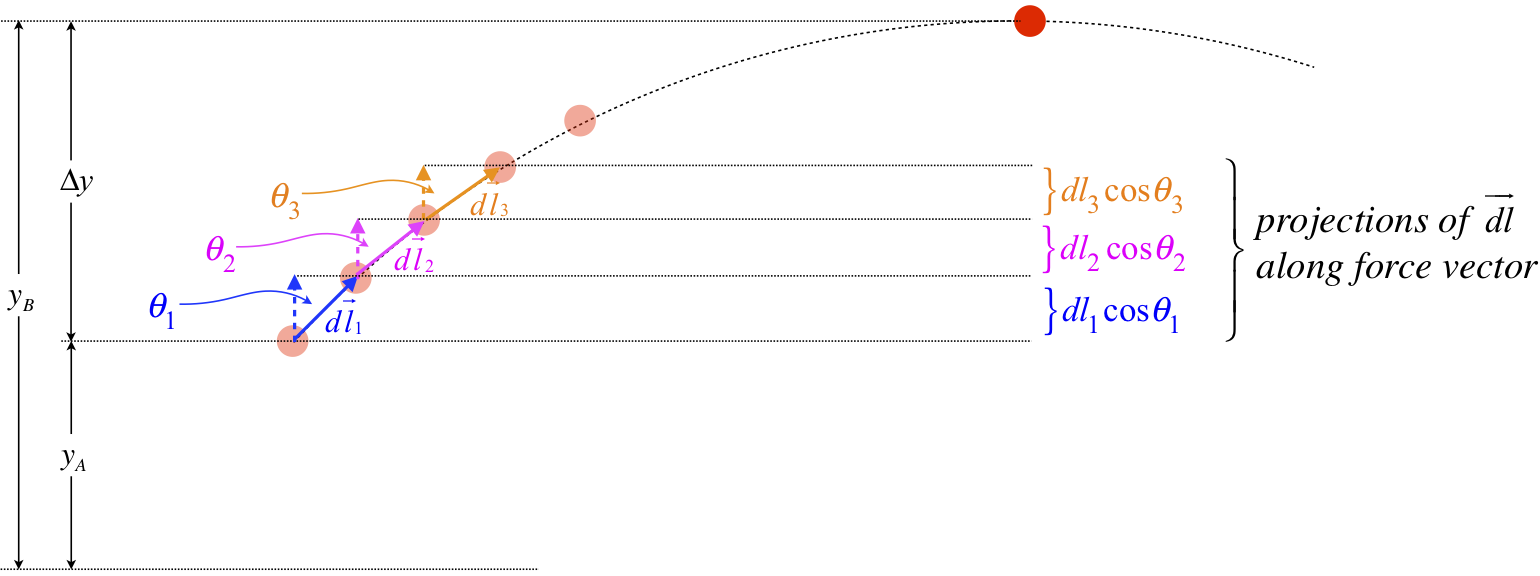
To compute the total work done by gravity as the ball rises to height \(y_B\) from \(y_A\), we add up all the dot products of the force with the tiny displacements. Each of these dot products equals the magnitude of the force and the projection of the displacement vector on that force. In this case, the force is down, and the projection is up, so a minus sign also appears. The result is:

\[ W_{grav} \left(A \rightarrow B\right) = \int \limits_A^B \overrightarrow F \cdot \overrightarrow {dl} = -mg \left( dl_1 \cos \theta_1 + dl_2 \cos \theta_2 + dl_3 \cos \theta_3 + \dots \right) = -mg \left( y_B - y_A \right) = -mg \Delta y \]

Now suppose that instead of a projectile, we look at the previous example of the block on the loop-de-loop.

Figure 3.2.2 – More Work Done by Gravity

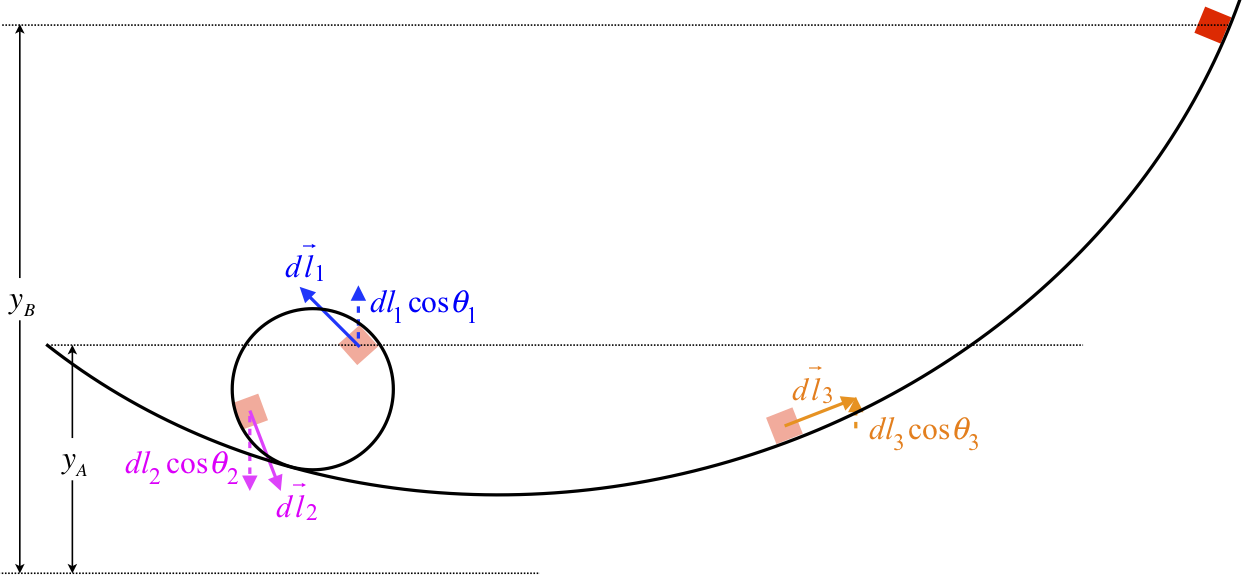
If we add up all the contributions to the work in this case, while we get some positive as well as negative contributions, we find the same result as before:

\[ W_{grav} \left(A \rightarrow B\right) = \int \limits_A^B \overrightarrow F \cdot \overrightarrow {dl} = -mg \left( dl_1 \cos \theta_1 - dl_2 \cos \theta_2 + dl_3 \cos \theta_3 + \dots \right) = -mg \left( y_B - y_A \right) = -mg \Delta y \]

We therefore get the remarkable result that the work done be gravity doesn’t seem to depend upon the path taken from point A to point B, but only depends upon the positions (specifically, the heights) of those points. We could do the same analysis for the pendulum, and get the same answer. This property of the work done depending only on the endpoints is not true of all forces, but those forces for which this property holds are called conservative forces (we’ll see where this name comes from shortly). Notice that an object that comes back to the position where it started (i.e. follows a closed path), no matter how crazy the route it takes might be, will have no net work done on it by a conservative force. We can represent this abstractly by:

\[ W_{conservative\;force} \left( A \rightarrow A \right) \equiv \oint \overrightarrow F \cdot \overrightarrow {dl} = 0 \]

The circle in the integral sign means “around a closed path.” Let’s show this property explicitly for gravity.

Figure 3.2.3 – Round Trip Work Done by Gravity

Elastic Force is Conservative

There is a force we have only discussed very briefly that we should also look at – the elastic force. Recall that this force obeys Hooke’s law:

\[ \overrightarrow F _{elastic} = - k \Delta \overrightarrow x, \]

where the magnitude of \(\Delta \overrightarrow x \) is the amount that the spring is stretched from its equilibrium position. Let’s compute the work done by a spring on a block as the spring is compressed. In Figure 3.2.4, \(x=0\) represents the position where the spring is at its equilibrium length.

Figure 3.2.4 – Work Done by a Compressing Spring

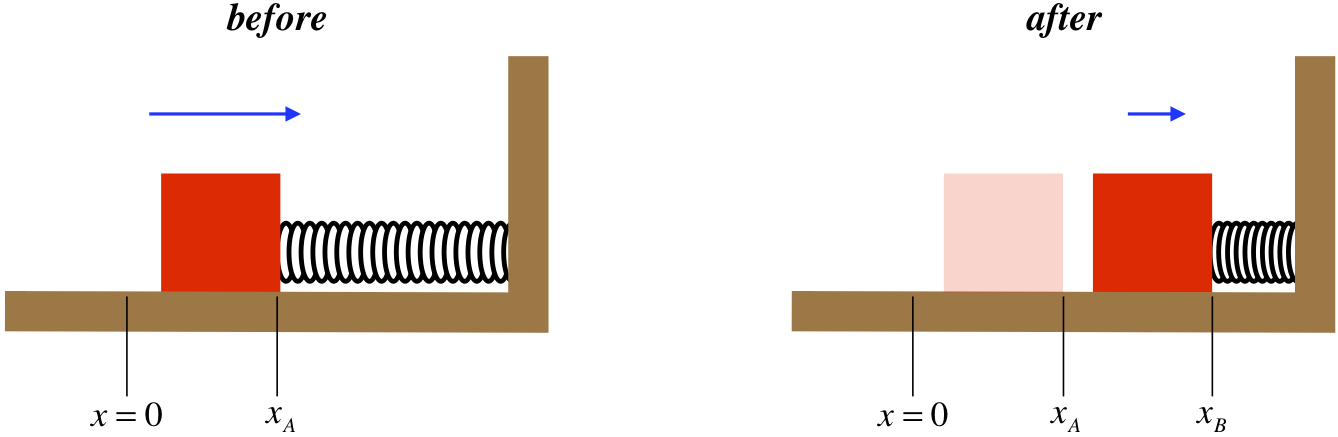
\[ W_{spring} \left( A \rightarrow B \right) = \int \limits_A^B \overrightarrow F \cdot \overrightarrow {dl} = \int \limits_A^B \left(-kx \widehat i \right) \cdot \left(dx \widehat i \right) = -k \int \limits_A^B xdx = \left[ -\frac{1}{2}kx^2 \right]_A^B = -\left[ \frac{1}{2}kx_B^2 - \frac{1}{2}kx_A^2 \right] = - \frac{1}{2}k\Delta \left( x^2 \right) \]

While this result isn’t exactly the same as that for gravity (the work done depends upon the change of a quadratic rather than a linear function), it is strikingly similar in that the result only depends upon the endpoints. We therefore conclude that this force is also conservative. We can check the round-trip criterion easily enough to be sure. If we move the block from the equilibrium point to the right, compressing the spring, and then back to the equilibrium point, the force always points left, while the displacement vectors reverse direction, giving:

Figure 3.2.5 – Round Trip Work Done by Spring

Kinetic Friction is Not a Conservative Force

Let’s have a look at kinetic friction next. We’ll choose a simple situation – a block sliding on a horizontal rough surface. In this case, the kinetic friction force always opposes the motion of the sliding object, which means the force is always opposite to the displacement vector. This prevents the round-trip cancelation of work that we saw for the cases of gravity and elastic force.

Figure 3.2.6 – Round Trip Work Done by Kinetic Friction

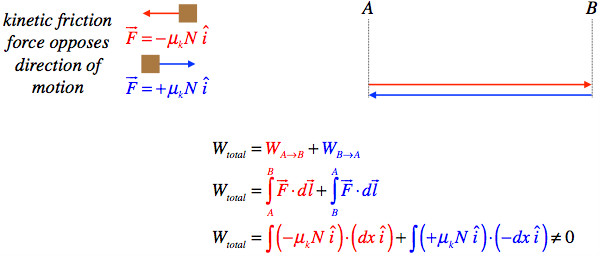
We see that in fact the kinetic friction force does not result in zero work done for a closed path. This is an example of a non-conservative force. Unlike gravity and the elastic force, work done by the kinetic friction force does not simply depend upon the starting and ending points of the object’s motion, but rather depends upon the path followed.

Alert

It only takes one example of the work calculation being dependent upon the path to demonstrate that a force is non-conservative, but to declare a force to be conservative, the work done must be independent of the path for all paths. This makes rigorously proving a force is conservative a bit tougher than proving one is non-conservative. Fortunately, in practice it's unusual to find a force that does the same work for two paths with common endpoints, while it does a different amount of work for other paths between those endpoints.

ExAmple \(\PageIndex{1}\)

Show that the force given below is not conservative by computing the work done it would do on an object that moves from the origin to the point (1,1) in the \(x\)-\(y\) plane for two different paths. The first path goes across-then-up ("atu") – it follows the \(x\)-axis from the origin to the point (1,0), then goes parallel to the \(y\)-axis up to (1,1). The second path goes up-then-across ("uta") – it follows the \(y\)-axis to the point (0,1), then goes parallel to the \(x\)-axis over to (1,1).

\[ \overrightarrow F \left(y \right) = \alpha y \widehat i \nonumber \]

Solution

For the atu path, in the entire first leg (along the \(x\)-axis), the value of \(y\) is zero, which makes the force magnitude zero. So there is zero work done by this force in this leg. Then in the second leg of the atu journey, the force magnitude is no longer zero (as \(y\) grows from 0 to 1), but the force points in the \(+ \widehat i \) direction, which is perpendicular to the direction of motion which is in the \(+ \widehat j \) direction), resulting in a zero dot product. Therefore the force does no work during this leg also, which means no work at all is done for the atu path.

The first leg of the uta path is the same as the second leg of the atu path - the force is perpendicular to the direction of motion, and therefore does no work. In the second leg of the uta path, however, the value of y is 1 (not zero), and the force points in the same direction as the motion, so there is some positive work done during this leg. There is therefore some work done over the uta path, but not over the atu path, which means that the work done is path dependent, and the force is non-conservative.